2018年北京卷(理科)第19題的推廣
2019-06-11 12:47:40曾立梅胡芳舉
中學數學研究(江西) 2019年5期
關鍵詞:拋物線
曾立梅 胡芳舉
湖南省桃江縣第一中學 (413400)
2018年北京卷(理科)第19題為:
已知拋物線C:y2=2px經過點P(1,2),過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.
(Ⅰ)求直線l的斜率的取值范圍;

解:(Ⅰ)略;(Ⅱ)由題設知:拋物線C的方程為y2=4x.
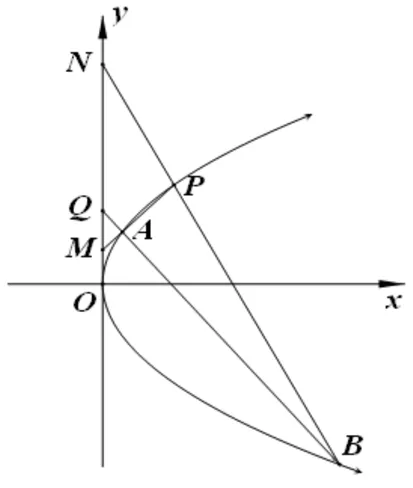
圖1
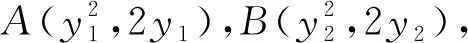

注意到直線QP與拋物線C相切,于是可將該題作如下推廣:

圖2

證明:以O為原點,OQ為x軸建立直角坐標系.設直線AB的方程為x=ky,點P(x0,y0),Q(m,0),A(ky1,y1),B(ky2,y2).

原點O與直線PQ是一對極點極線,由此可得直線PQ的方程為dx+ey+2f=0.將點P(x0,y0),Q(m,0)代入以上方程得dx0+ey0+2f=0,dm+2f=0(*).

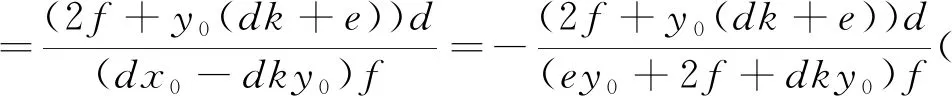

猜你喜歡
中學生數理化·高二版(2025年2期)2025-03-05 00:00:00
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:58
中學生數理化(高中版.高二數學)(2022年1期)2022-04-26 13:59:56
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
中學生數理化(高中版.高二數學)(2021年3期)2021-06-09 06:08:40
中學生數理化(高中版.高二數學)(2021年2期)2021-03-19 08:54:12
中學生數理化·中考版(2019年10期)2019-11-25 09:39:04
中學生數理化·中考版(2018年10期)2018-12-07 00:44:42
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38

