以“問”和“導”構建有效生本課堂
——從浙教版八上《2.4等腰三角形的判定定理》教學說起

隨著新課改的不斷深入，基于學生學習力發展的課堂教學方式也隨之發生了顯著變化。“以生為本、學為中心；以學定教、順學而導”的教學理念已成為課堂的主旋律。教師教學的著力點也從關注教師如何“教”轉變為關注學生如何“學”，放大“學”，優化“導”，做到“學”與“導”的合理契合。而“智慧導學”作為“學導課堂”五大核心要素之一，是“學導課堂”得以有效實現的前提和重要保障，其相應的教學策略顯得尤為重要。它不僅需要教師在教學過程中有一雙慧眼來“相機”，而且需要有一顆智心來“導學”。筆者在八上《2.4等腰三角形的判定定理》這節課的教學中，細研教材，抓住提問時機，并順學而導，順利突破重、難點，達成教學目標。現例說如下。

一、尊重教材，經歷過程，充分體驗

任何的數學教育教學活動都是以培養學生的數學素養為目的。就筆者來看，數學素養不同于數學知識，不是短期可以培養出來的。它依托于數學知識點，通過教師日常的教學活動，使學生養成習慣、形成經驗，并經過長期積累逐漸形成。在浙教版數學教材中，經常會安排讓學生畫一畫、量一量，旨在讓學生通過動手實驗，經歷發現知識、發現規律、驗證猜想等過程，引領學生體驗數學知識發生、發展的本質，學會理性思維，進而培養邏輯思維能力。如何理解教材、處理教材，如何教學設計值得思考。

案例1：浙教版教材八上《2.4等腰三角形的判定定理》教學片段一

1.教材背景

本節課是在學習了等腰三角形的定義和性質后的一節新授課，教材開頭就設問：“根據等腰三角形的定義，如果一個三角形的兩條邊相等，那么就可以判定這個三角形是等腰三角形。除此之外，還有其他判定方法嗎？”緊隨其后是合作學習環節，具體內容如下。

在紙上任意畫線段BC，分別以點B和點C為頂點，以BC為一邊，在BC的同側畫兩個相等的角，兩角的另一邊相交于點A。量一量，線段AB與AC相等嗎？其他同學的結果與你的相同嗎？你發現了什么規律？

2.教師教學設計

教師以復習等腰三角形的定義和性質作為課堂引入并提問：“同學們，由等腰三角形可以得到很多結論。反之，要判定一個三角形是等腰三角形，則需要具備什么條件呢？”

學生紛紛回答：“‘兩條邊相等'或者‘兩個角相等'。”

教師追問：“這兩種方法的依據分別是什么？”

學生回答：“是等腰三角形的定義和等腰三角形的兩個底角相等。”

教師：“回答得很好，定義既是性質又是判定，所以有兩條邊相等可以判定一個三角形是等腰三角形，接下來我們重點討論‘有兩個角相等'這種判定方法。同學們能夠從‘等腰三角形的兩個底角相等'這個性質，猜想到‘有兩個角相等的三角形是等腰三角形'這種判定方法值得肯定。說明同學們意識到知識是前后相關的。但請同學們再想一想，把一個真命題的條件和結論互換后，所得命題是否仍是真命題呢？”

學生回答：“不一定。”

教師追問：“請舉例。”

學生回答：“‘對頂角相等'的逆命題是‘相等的角是對頂角'，這是一個假命題。”

教師及時肯定所舉反例：“從剛才某某同學所舉例子中，同學們可以感受到‘等腰三角形的兩個底角相等'不能支持你們的猜想，你們是否感覺到這個‘顯而易見'的判定方法找不到依據？”

學生紛紛點頭，教師繼續闡述：“事實上，在兩千年前，幾何知識的鼻祖——古希臘數學家歐幾里得以及其他數學家，在研究數學發展的過程中，也會遇到有猜想卻找不到依據的情況。他們會怎樣處理呢？他們往往會通過動手實驗的方式來進一步驗證猜想。接下來，我們也學一學他們，一起來完成合作學習部分。”同時強調作圖工具不限。

學生馬上動手實驗，教師巡視。獨立完成后要求同桌之間互相交流：作圖具體步驟；作圖所用工具；線段AB與AC是否相等？如何判斷？最后讓作法有代表性的幾位學生在班級中分享。教師最后小結：“同學們用不同的方法完成了合作學習，從作圖痕跡可以判斷∠B=∠C。我們發現，只要∠B=∠C，我們都能得到AB=AC。此刻我們是否可以認為‘有兩個角相等的三角形是等腰三角形'就是定理了呢？”

學生：“不可以，作圖有誤差，不夠嚴謹。”

教師追問：“那怎么辦？”

學生：“推理，證明。”

教師：“那怎么來證明這個命題呢？接下來請同學們獨立思考，有想法舉手……”

在此教學環節中，根據等腰三角形的性質和判定定理的互逆關系，以及學生在小學階段對等腰三角形的認知與幾何直觀，學生較易猜想出“有兩個角相等的三角形是等腰三角形”這個判定方法。既然學生根據已有的認知有了這樣的猜想，那么緊隨其后的合作學習環節是否還有必要讓學生經歷？具體該如何處理？

顯然，教材安排合作學習的目的是讓學生經歷等腰三角形判定定理的發現過程。通過“經歷實驗——發現規律——給出證明”的過程，體驗發現、檢驗真理，培養數學思維品質。因此，即使學生根據已有的數學經驗得出正確的猜想，仍要引導學生經歷定理從發現到最后得以證明成立的整個過程。

另外，在合作學習過程中，教師補充強調的作圖工具不限及交流分享環節，讓學生充分感受到實驗途徑的豐富多樣性。而教師合作學習后的小結又讓學生“心甘情愿”地回歸于猜想，并在一問一答中引出判定定理證明的必要性。

因此，教師在備課過程中要仔細研讀教材內容，根據教學目標，領悟教材內容安排的用意，尊重教材。尤其重視設置的數學活動，并以此為載體，讓學生經歷過程，充分體驗。學生也只有經歷了數學活動的過程，才能不斷地生成、豐富、拓展、提升和交流數學活動的經驗，從而形成和發展數學核心素養。

二、追根溯源，強調本質，淡化形式

早在二十多年前，陳重穆、宋乃慶教授就提出了“注重實質、淡化形式”的數學教學理念。而當下的數學課程改革，也明確提出了“強調本質，注意適度形式化”的教學理念。因此，教師在教學過程中，不僅對教學內容和目標要有正確的定位，在教學設計中，還需順應學生思維發展，注重強調數學本質，淡化形式。

案例2：浙教版教材八上《2.4等腰三角形的判定定理》教學片段二

證明等腰三角形的判定定理——如果三角形的兩個角相等，那么這個三角形是等腰三角形。

學生通過分析命題的條件和結論，經過交流和補充，給出以下證明：

已知：如圖，在△ABC中，∠B=∠C

求證：△ABC是等腰三角形

證明：作角平分線AD

∴∠1=∠2

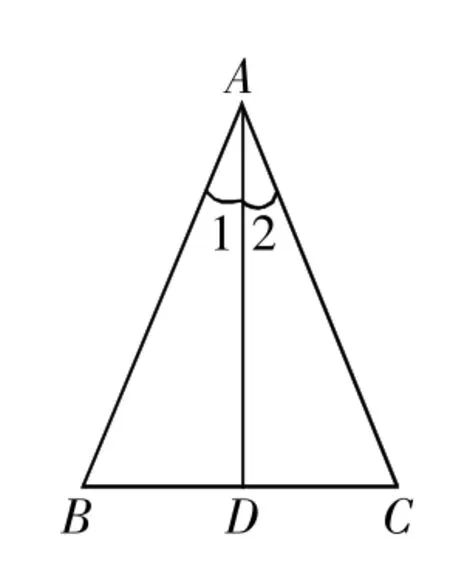
∴△ABD≌△ACD(AAS)∴AB=AC ∴△ABC是等腰三角形

此時，教師追問：“你是怎么想到添這條輔助線的？”

學生回答：“想要證等腰三角形，只要證明AB=AC。即證明兩個三角形全等，所以想到了添這條輔助線。”

教師：“某某同學的想法你們同意嗎？”

學生：“同意。”

教師追問：“依據是什么？”

學生：“等腰三角形的定義。”

教師：“同學們說得很好。另外，看某某同學的證明過程，主要是運用了全等三角形這一舊知。這種用已有的知識來解決新問題的思想方法是研究數學問題的基本策略。同學們還有其他不同的證明方法和大家分享嗎？”

有同學提出高線并證明……

在實際教學中，教師在教學過程中不向學生追問輔助線添法的來源，而是追求證明方法的多樣化，甚至主動補充當AD是中線時的證明方法。顯然，這種做法教師是以俯視的姿態告訴式地展開教學。只注重知識的灌輸而忽視了學生的認知起點，在學生思維的生成上沒有追根溯源，淡化了考慮問題“從哪里來，要到哪里去”的數學本質，也偏離了教學目標。

三、順應思維，因勢利導，提煉歸納

著名數學家波利亞曾告誡我們：“讓你的學生提問題，要不就像他們自己提問的那樣由你去提出這些問題；讓你的學生給出解答，要不就像他們自己給出的那樣由你去給出解答。”的確，在課堂上，教師要順應學生思維并善于設問，啟發學生思考，引導學生獨立或合作解決問題，把課堂真正還給學生。

案例3：浙教版教材八上《2.4等腰三角形的判定定理》教學片段三

在證明完等腰三角形的判定定理后，教師提出：“等邊三角形又該如何判定呢？”

學生紛紛回答：“‘三邊相等'，‘三個角相等'。”

教師追問：“依據分別是什么？”

學生回答：“三邊相等是根據等邊三角形的定義，三個角相等找不到依據。”

教師：“找不到依據，那你能推理證明嗎？”

學生：“能。”證明過程具體如下：

∵∠A=∠B=∠C

∴AB=AC=BC

即△ABC是等邊三角形

教師：“由三角相等推出三邊相等的依據是什么？”

學生：“等腰三角形的判定定理。”

教師：“某某同學說得非常好！只要在同一個三角形中，角相等就能推出所對的邊相等。這個定理對角的個數是兩個還是三個沒有規定。”

隨之得出等邊三角形的判定定理1：三個角相等的三角形是等邊三角形。

教師繼續問：“如果已知等腰△ABC，且AB=AC，證明它是等邊三角形，還需增加什么條件？請說說你的想法。”

學生充分議論，最后一致反饋為：①AB=BC ②∠A=60°③∠A=∠B ④∠A=60°

教師結合圖形引導學生逐一說明四種條件成立的理由，特別對方法②和④進一步追問，引導學生說清楚求其他兩個角的方法的不同之處。

接著，教師繼續追問：“請同學們把剛剛增加的4種不同的條件轉換成文字語言并填空，使之成為一個真命題。”_____________________________________的等腰三角形是等邊三角形。

學生交流后概括為：①腰與底邊相等，②頂角等于底角，③有一個角等于60°。

教師：“同學們概括得很好，接下來讓我們一起來理一理你們剛才得出的三個真命題。”

①腰與底邊相等的等腰三角形是等邊三角形。它的實質就是三邊相等的三角形是等邊三角形，即等邊三角形的定義。

②頂角等于底角的等腰三角形是等邊三角形。它的實質就是三角相等的三角形是等邊三角形，即等邊三角形的判定定理1。

③有一個角等于60°的等腰三角形是等邊三角形。這個真命題我們還沒有推理證明，這就是本節課要學習的等邊三角形的判定定理2……

在上述教學設計中，教師能順應學生從等腰到等邊的思維發展，設置一個個問題，在循循善誘中引導學生類比學習等腰三角形過程中的思想方法，猜想、推理證明等邊三角形判定定理1。同時，在推理證明等邊三角形判定定理2的教學設計上，教師設問起點低且開放，滿足了所有學生的“胃口”，充分調動了學生的積極性。引導學生由圖形語言慢慢過渡到文字語言，由淺入深、循序漸進。學生既能獨立思考，又能合作探究，充分經歷了觀察、比較、歸納、整理、證明的數學學習過程，并從中體會到了分類討論思想。而最后，師生一起通過歸納整理，使等邊三角形的判定定理2自然生成，也使等邊三角形的相關內容得以提煉歸納，使本節課的難點得以順利突破。

教師在教學過程中，不應以知識豐富而自居，而應善于把自己已有的知識擱置一旁，把自己的思維降低至學生的思維水平，有意識地退回到與學生相仿的思維狀態。并根據學生的思維起點和發展規律，結合教學實際相機而問，順學而導。在問中把學生推向“前臺”，成為課堂主角，彰顯學生學習的“主權”；在導中引領學生經歷知識發生、發展、生成的過程，積累數學活動經驗，提高數學思維品質，進而培養數學核心素養。總之，教師在日常教學中，在認真研讀教材，領會教材編寫意圖，明確重難點的同時，要善于抓住“問”的時機，明確“問”的方向，思學生所思，難學生所難，真正構建有效生本課堂。