運動覓本質 變化提素養

浙江省平湖中學

李學軍 (郵編：314000)

浙江省慈溪中學

苗孟義 (郵編：315323)

浙江省鎮海中學

沈虎躍 (郵編：315200)

源起2018年11月26日，浙江省教育廳“百人千場”高中數學專家名師赴磐安縣送教活動中，沈虎躍名師網絡工作室學科帶頭人慈溪中學苗孟義老師在磐安二中開設了一節課題為《立體幾何動態問題復習》高三一輪專題復習課，這節示范課使學生主動深入探究環境當中，在恰當的時機給學生創造自由飛翔的空間，有效地激發了學生的學習潛能，使得各種層次的學生都能夠學有所獲.苗老師的這節課設計樸實而有針對性，選題精煉而有代表性，在充分尊重學生的同時，又激發了學生對問題解決的熱情，下面簡要回顧課堂教學的部分環節以及自己的切身感受，談一下自己對課堂教學的思考.

1 教師主導——駕馭課堂真老師

苗老師在知識復習階段，回顧了余弦定理及余弦定理的變形，接下來從余弦定理出發，向平面向量過渡，通過平面向量公式的變形，逐步探究出本節課的主干知識，在這個探究的過程中，既要兼顧到教材概念、思想、方法的回顧，又要把相互關聯的概念、思想和方法有機地串聯起來，使學生能夠達到真正意義的融匯貫通.

課堂實錄1對角線向量定理的探究

師：余弦定理可以寫成向量的形式嗎？

師：兩式相減，左邊等于什么？

師：右邊等于什么？

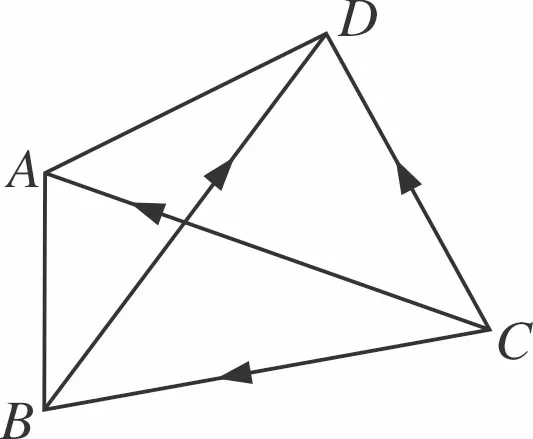
圖1

師：同學們發現這個公式中字母的規律了嗎？

生：由內及外再交叉相減.

師：這個定理就叫做對角線向量定理，有些書上也叫做四點向量定理；對角線向量定理，表明四邊形的兩條對角線對應向量的數量積可用四條邊的長度表示.

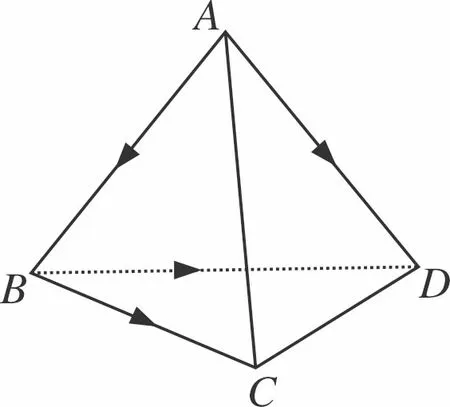
圖2

師：今天我們研究的主要內容是立體幾何中的動態問題，因此這個四邊形要進行翻折，對不對？

師：假如我們以BD為軸進行翻折，這樣平面問題轉換為空間問題，同學們思考一下，在空間中，對角線向量定理是否成立？

生：在翻折的過程中，四條邊的長度沒有發生變化，因此在空間四邊形中，對角線向量定理仍然成立；

感悟《普通高中數學課程標準(2017版)》中說“教師應理解不同數學學科素養水平的具體要求，不僅關注每節課的教學目標，更應關注主題、單元的教學目標，明晰這些目標對實現數學學科素養發展的貢獻.”苗老師的這個環節從學生的最近發展區出發到知識理解，知識遷移，知識創新層層遞進.真正體現了“整體設計必修和選擇性必修課程的體系，處理好數學內容的層次性與數學學科核心素養水平發展的連續性”.在高三的一輪復習中從教材出發進行追本溯源，挖掘知識的本源，滲透必要的數學核心素養，這樣的復習為后續的綜合能力的提升奠定了非常扎實的基礎.

2 學生主體——課堂掌控真主人

圖3

A.存在某個位置，使得直線AC與直線BD垂直

B.存在某個位置，使得直線AB與直線CD垂直

C.存在某個位置，使得直線AD與直線BC垂直

D.對于任意位置，三對直線“AC與BD”，“AB與CD”，“AD與BC”均不垂直

課堂實錄2對角線向量定理的理解

師：請同學們用自己所帶的紙折一下，然后猜猜看或者用我們剛剛探究過的對角線向量定理.

(巡視和學生交流是猜的選項B，還是算出來的)

師：對于選項A如何判斷？

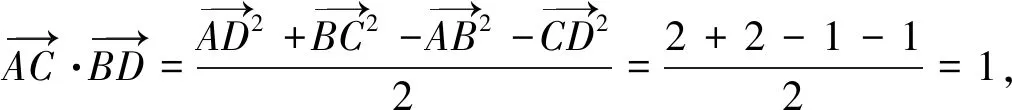
師：對于選項B呢？

圖4

師：最大值是多少呢？

師：最小值如何求呢？

生：當翻折后與A、B、D共面時最小.

師：如何求此時的AC′的長度呢？翻折后AC′與BD有什么關系呢？

師：在平時的學習中，我們要對每一個選項進行深究一下，選項C如何判斷呢？

師：如果這種方法，在平時你一直在用，那么在大型考試中遇到這樣類型的小題你就可以進行秒殺了.

感悟這個題目是2012年浙江高考數學理科的第10題，苗老師在課堂上引導學生動手折一折，實際上就是培養學生因地制宜，充分利用周圍的環境解決問題，通過數學實驗直觀的發現答案.接下來苗老師“話風”一轉，數學講究嚴謹性，引導學生通過計算的方式進行嚴格推理論證.學生在苗老師的引導下，緊張有序的進行逐個選項的論證.雖然這是高三的一輪復習，但是苗老師在課堂上給學生留出足夠的時間，讓學生對所學習的知識進行去思，去悟，去用，真正實現了學以致用.

3 課堂主場——滲透素養真領地

圖5

課堂實錄3對角線向量定理的內化

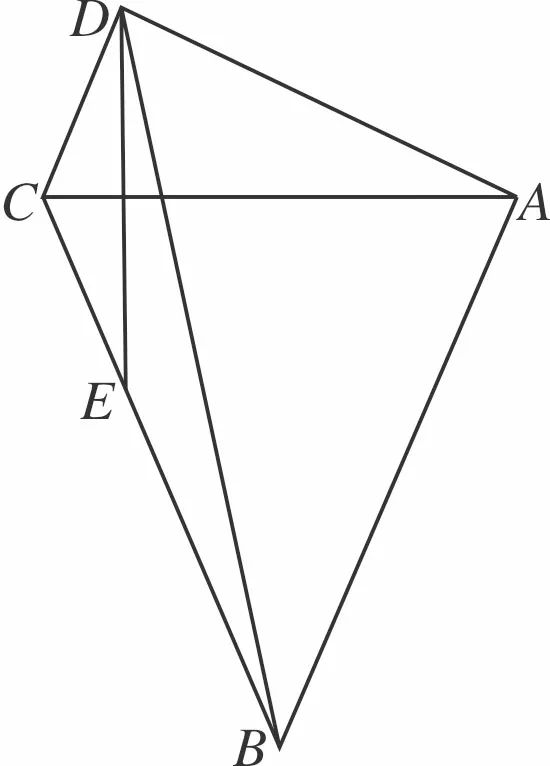
圖6

生：∠ACD=∠BCD，

師：請問，cos∠BCD等于多少？

生：cos∠BCD=cos2∠ACD=

師：在平面四邊形ABCD中，你會求BD的長度嗎？

師：當點D在什么位置時，BD的長度最小？

生：當點D′落在BC的三等分點E處時BD′=3-1=2最小.

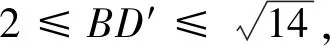
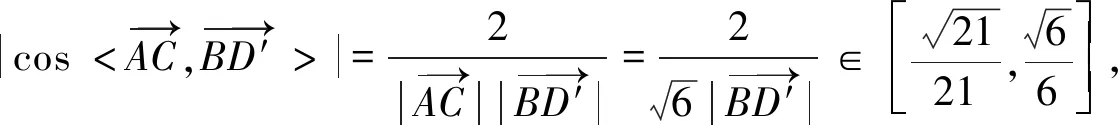
感悟《普通高中數學課程標準(2017版)》中提出“數學學科素養包括：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析.這些數學核心素養既相對獨立、又相互交融，是一個有機的整體.”在標準中還給出了核心素養的水平劃分的三個層次具體的要求，因此在課堂教學中，苗老師根據學生的現有的學習能力，引導學生主動地參與學習，培養學生用數學思維和習慣進行學習，通過較為復雜的數據運算，取值范圍的求解，翻折過程中的動態變化，使得數學運算，邏輯推理，直觀想象等數學核心素養有效扎實地落到實處.

圖7

4 問題主線——能力提升真效果

例3(2015年浙江省普通高中學業水平考試數學試題18題)如圖，在菱形ABCD中，∠BAD=60o，線段AD、BD的中點分別為E、F，現將△ABD沿對角線BD翻折，則異面直線BE與CF所成角的取值范圍是( )

圖8

課堂實錄4一類問題的多種思維

師：這是一個選擇題，你有沒有辦法猜出答案呢？

師：通過特殊值法進行定性分析是有風險的，如果題目中有陷阱就比較麻煩，接下來，我們進行定量計算，不妨設菱形ABCD的邊長為2.

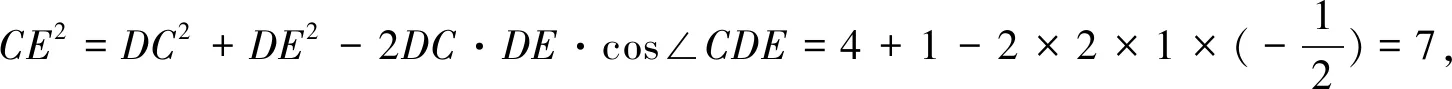
師：非常棒！事實上當△ABD沿對角線BD翻折的過程中，點E的軌跡是是什么？

生：是一個圓.

師：線段BE在翻折的過程中的軌跡是什么？

生：是圓錐的側面.

師：請同學們課后思考一下，你可以通過這樣的思路解決這道題嗎？

教學啟示

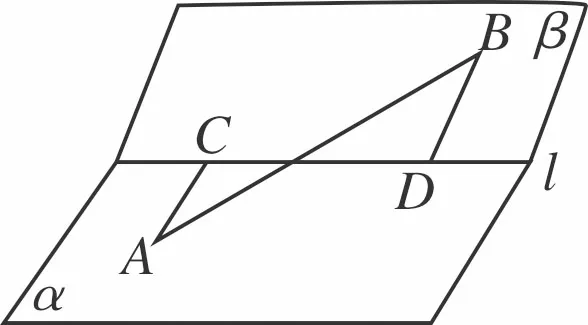
圖9

(1)關注教材的潛力

數學選修2-1第106頁例2如圖，甲站在水庫底面上的點A處，乙站在水壩斜面上的點B處.從A、B到直線l(庫底與水壩的交線)的距離AC和BD分別為a和b，CD的長為c，AB的長為d.求庫底與水壩所成二面角的余弦值.

在解決這個問題我們可以從三個層次進行探究.

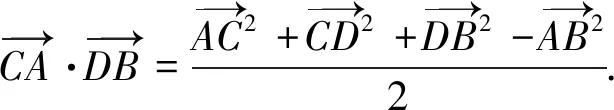
第三層次：再推廣一下當AC，BD與CD不垂直時，

正如葉圣陶先生所說：“教材無非是個例子，它只能作為教課的依據.要教得好，使學生受益，還要靠教師善于運用.”事實上在我們的教材中，只要我們做個有心人，用心去挖掘這樣的素材，一定可以從不同角度得出更多有意義的結論，使得我們課堂更加韻味無窮.

(2)關注專題的實效

對角線向量定理，可以快速解決一類關于向量數量積或向量夾角問題，但并不是一味追求高難度的解題技巧，恰恰相反，通過這種專題的探究，尋求一類問題的通解通法，進而形成一類問題的統一解法.事實上對于動點的軌跡問題苗老師的這節課完全可以設計動畫演示，通過動畫學生對動點的運動狀態理解可能會更加深刻，尤其對空間想象能力不強的學生來說效果會更好.但是高三復習目的是讓學生在考場上能夠在有效的時間內對所考查的問題進行有效解決，因此在高三的復習課堂就應該為這樣的目的進行設計和實施.

(3)關注考題的聯系

考題1(2014年1月浙江省普通高中學業水平考試第25題)如圖，在Rt△ABC中，AC=1,BC=x，D是斜邊AB的中點，將△BCD沿直線CD翻折，若在翻折的過程中存在某一時刻，使得CB⊥AD，則x的取值范圍是( )

圖10

圖11

圖12

考題2(2009浙江高考理科第17題)如圖，在長方形ABCD中，AB=2,BC=1，E為DC的中點，F為線段EC(端點除外)上的一動點.現將△AFD沿AF折起，使平面ABD⊥平面ABC，在平面ABD內過點D作DK⊥AB，K為垂足.設AK=t，則t的取值范圍是.

這樣背景的試題在高三的復習資料中會經常出現，在解決問題的過程中，我們也應該關注這些試題之間是否存在共性的東西，解決這類問題是否有行之有效的共性辦法，這也就是數學中的合情推理和演繹推理的最好落實.正如波利亞曾形象地指出“好問題同某些蘑菇有些相似，它們大都成堆地生長，找到一個之后，你應當在周圍再找一找，很可能就有幾個”.

總之，數學教學不僅要教授數學知識，數學方法，更要引導學生把握數學內容的本質，發展學生的數學核心素養，用數學的眼光看問題.張奠宙教授曾經說過：“數學教學的有效性關鍵在于對數學本質的把握、揭示和體驗.”在教學中要想更好的駕馭時刻在變化的課堂，就需要老師在平時不斷提升自身的數學素養，從而實現真正意義的教學相長.