問題驅動 引導深度教學
——以“排列”教學為例

徐 睿

(江蘇省昆山中學 215300)

我們在每天的教學中都會思考這樣的問題：如何提高學生學習的學習興趣？如何激發學生的積極性與主動性？如何使課堂效率更高？當學生對課堂產生了好奇、疑問，自然就有了學習動機，對學習產生了興趣.課堂教學若能科學而又有藝術地設計一些能解決核心問題的問題，就能調動學生的積極性.

一、教材分析

“排列”是蘇教版《數學選修2-3》第一章第二節課，教科書通過具體實例歸納出排列的概念，再運用分步計數原理得到排列數公式.排列以計數為主要內容，它不僅應用廣泛，能為學習統計、概率及高等數學有關分支準備知識基礎，同時也能大大提高學生的抽象思維和邏輯思維能力，為解決很多實際問題提供了思想和工具.

本節課具有承上啟下的地位，它既是分步計數原理的應用，又為學習組合和組合數公式奠定了基礎，而且與后面概率中的二項分布有著密切聯系.

二、學情分析

學生剛學過兩個基本計數原理，遇到計數問題往往能夠往分類或分步的方向進行思考.學生對生活中比如排隊、接力賽、活動參與等計數問題有了一定的經驗，有運用化歸思想、特殊到一般的思想解題的意識，但抽象概括能力不強，對于排列概念的得出需要在獨立思考和討論協助的基礎上，再由老師引導解決.

三、教學目標

理解排列的意義，掌握排列數的計算公式，并能運用公式解決簡單的排列問題，經歷排列數公式的推導過程，感受特殊到一般的思維方式在數學中的應用，提升抽象概括能力，邏輯思維能力，體會知識在實際生活中的應用，增強學生學習數學的興趣.

四、教學重點、難點

教學重點：排列、排列數的定義，排列數公式的推導.

教學難點：排列數在實際問題中的應用及解決實際問題時的思路分析.

五、教學策略選擇

為更好地突出重點，培養學生抽象概括的能力，本課采用以問題為背景，引導啟發，通過創設情境，設置問題串，通過大量的實例讓學生更深刻地理解概念， 學生獨立思考，相互討論，老師引導解決的過程，讓學生體會知識的形成和發展，通過觀察、歸納、思考、探究、交流、反思進一步培養學生解決實際問題的能力.

六、教學過程

1.問題情境，引出課題

問題1 現有高一學生4名，高二學生5名，高三學生3名，從中任選1人參加學生代表大會，有多少種不同的選法？若從每個年級的學生中各選1人參加學生代表大會，有多少種不同的選法？上述計數方法有什么區別？

問題2 現請同學們來解決如下兩個問題：

(1)若從6名志愿者中選出4人分別從事翻譯、導游、導購、保潔四種不同的工作，有多少種不同的選派方案？

(2)從3名學生中選出2名分別擔任班長和團支書，有多少種不同的選法？

問題3 上面兩個問題的共同點是什么？

設計意圖：問題1復習分類和分步兩個基本計數原理，為新知識學習奠定基礎.通過問題2、3討論上述兩個問題的共同點，給出排列的一個模糊概念：像這樣的問題中研究的模型就是排列，并引出課題.

2.概念辨析，強化理解

問題4 以下問題是排列問題嗎？

(1)從甲、乙、丙、丁四個人中選取2個人參加團代會的選取方案有多少種？

(2)在四張卡片上分別印有o,o,k,k，現選擇2張卡片按左右擺放在一起，可以組成哪些不同的結果？

(3)從6人中選4人參加4×100m接力賽，有哪些選派方案？

(4)在平面直角坐標系中，由互不相等的四個數a,b,c,d組成的點的坐標有哪些？

設計意圖：通過具體實例進一步體會怎樣的模型是排列，加深對排列的理解，正面強化排列問題中的兩個關鍵點“不同元素”和“按照一定順序”，為后面歸納得出排列的概念做好準備.

3.抽象概括，概念生成

問題5 上面的(3)(4)可提煉為如下兩句話：

(3′)從6個不同元素中取出4個元素，按照一定順序排成一列；

(4′)從4個不同元素中取出2個元素，按照一定順序排成一列.

請問同學們能否將它們推廣到一般情形？

學生討論、歸納、總結、完善，得出排列的定義.

例1寫出從a,b,c,d這4個字母中，取出2個字母的所有排列.

學生利用列舉法或樹形圖寫出所有排列，并數出了所有排列的個數.

問題6 像“ab,ac,…”這些我們稱什么？“12”又是什么？

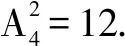
變1：從a,b,c,d這4個字母中，取出3個字母的所有排列有多少種？

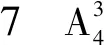
學生分組討論作答，有用列舉法，有畫樹形圖，有用分步計數原理求解，最后都能得到答案24.

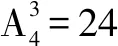
變2：從a,b,c,d這4個字母中，取出4個字母的所有排列有多少種？

教師適當引導，一方面用排列數的定義表示，另一方面用分步計數原理得到結果，異曲同工，體現了數學中的“算兩次”思想，為后面的學習鋪墊.

4.揭示規律，導出公式

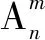
學生分組探究，歸納總結：完成這件事情，可以把這m個元素所排列的位置劃分為第1位、第2位、…，第m位，然后按照分步計數原理可得到排列數公式.

5.強化公式，跟進新公式

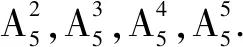
問題10 同學們做出答案后，有何數學發現？

七、教學反思

1.預設有效問題，發展學生思維

“思”源于“問題”，通過問題解決能使學生獲得知識、方法、能力及思想上的全面發展，所以課堂不能是任務驅動，而應是問題驅動，讓學生不僅關注怎么做，更要關注為什么要這樣做、怎樣才能想到這樣做，這有助于學生的思維發展.本節課用10個問題把課題引入，概念生成，公式導出等所有環節串在了一起，既完整又自然，一改以往的灌輸式教學.學生在這樣的問題課堂中，探究問題，討論問題，引發新問題，思維高度集中，學習的目標和方向進一步明確，從而激發學生學習的興趣；從教師角度看，設置有效問題的課堂能讓教師更好地把握知識本質，促進教師的專業發展.

2.關注互動交流，引發數學思考

建構主義學習觀認為，學習數學的過程實際上是個再創造的過程.學生帶著原本的知識和經驗走進課堂，經歷了自己的獨立思考，教師的引導，師生的互動交流活動，進而對知識有了更深入的理解.本節課以學生為主體，給學生充分的時間去思考討論研究，調動學生全員參與，激發了學生學習的積極性.例如在生成排列概念時，通過問題4的幾個具體實例，讓學生自己歸納總結，剛開始，往往在“不同元素”，“按照一定順序”等關鍵細節方面忽視了，經過后面幾位學生的不斷補充、完善，排列的概念自然而然就提煉出來了.又如，在揭示排列數公式時，并沒有直接將公式拋出，而是讓學生小組討論，自己去探究發現公式并嘗試證明.課堂上，要讓學生親歷數學過程，主動建構新知，讓學生相互交流，溝通，給學生自己動腦思考的空間，讓所有的學生獲得自我表現的機會.

3.培養核心素養，提高學生能力

培養數學抽象的素養有助于學生形成理性思維.本節課通過具體實例的對比，從事物的相異中抽象出一般規律，引導學生歸納、完善排列的概念，在實際生活的情境中幫助學生更好地理解知識，這個探索的過程有利于學生養成一般性思考問題的習慣.

排列數公式的推導證明，培養了學生直觀想象，數學運算的核心素養.

數學建模是對現實問題進行抽象，用數學語言表達和解決實際問題的過程.在引出排列的模糊概念時，用的問題2的模型：像這樣的的問題中研究的模型就是排列.自然的激發學生去思考如何完善模型.數學建模的過程是不斷反思的過程，能讓學生運用已學知識分析解決實際問題，從而培養學生解決實際問題的能力.對于教師而言，根據學生不同的建模方法，更好的優化教學設計，促使教師對教學的不斷思考.