20世紀以來中國中學數學課程中數學表征能力的發展趨勢與啟示——以幾何為例

李 娜，張晉宇，沈 陽

?

20世紀以來中國中學數學課程中數學表征能力的發展趨勢與啟示——以幾何為例

李 娜1，張晉宇2，3，沈 陽1

（1．華東師范大學 數學科學學院，上海 200241；2．華東師范大學 教師教育學院，上海 200062；3．上海市“立德樹人”數學教育教學研究基地，上海 200241）

依據20世紀以來中國各年代的中學數學課程標準（大綱），采用文本分析法，從表達交流、操作轉換和建模應用3個水平構建數學表征能力的水平分析框架．分別對初、高中數學課程標準中的平面幾何、立體幾何教學內容進行分析，進而探討20世紀以來，數學表征能力在中國不同時期中學數學課程標準中的發展趨勢以及獲得的啟示．結果表明，在數學表征能力方面，中國中學幾何課程標準對操作轉換的要求逐步上升，對表達交流的要求相對穩定，而對建模應用水平關注較少，課改后期開始才得到一定重視．

數學表征能力；中學數學；課程標準；教學內容；幾何

眾所周知，數學表征能力是學生數學核心能力之一，也是許多國家數學教育課程改革中備受關注的核心能力之一．從2000—2018年，PISA評估框架中表征能力一直是將其作為評價學生數學能力的重要指標之一，而且2018年的框架尤其強調數學表征能力的重要性．目前，很多研究者圍繞教師的教學、學生的學習、問題解決以及水平劃分等方面對數學表征能力展開了相關的研究[1-4]．中小學數學課程標準是中小學教師教學和學生學習的最重要的依據，但未發現圍繞20世紀以來數學課程標準文本中數學表征能力發展趨勢的相關研究．以平面幾何和立體幾何為例，探討20世紀以來，數學表征能力在中國不同時期中學數學課程標準中的發展趨勢以及啟示．

1 研究設計

1.1 概念界定

表征在《辭海》中兩種含義：其一為提示、闡明，其二為事物顯露外在的征象[5]．如果說《辭海》中“表征”的解釋包羅萬象，那么加了學科色彩的“數學表征”的內涵將進一步縮小．《數學教育百科全書》講述了數學表征的3層含義，其中教育界最常見的解釋為：“數學表征是可見的或有形的產物，例如圖表、數軸、圖形、具體對象或操作的排列、物理模型、數學表達式、公式和方程、或者計算機（器）屏幕上的描繪——編碼、代表或體現數學思想或聯系．”[6]美國《學校教育原則與標準》（2000）對數學表征有如下解釋：“術語‘表征’既指過程又指結果．換句話說，是指用某種形式表達數學概念或關系的行為，也指行為本身．”[7]而PISA則將其定義更加具體化，即“包括圖像、表格、圖表、圖片、方程式、公式和具體材料”[8]．

從形式上來看，數學表征的形式是靜態的，而相對于前者，數學表征能力是動態的．徐斌艷（2013）將數學表征和變換能力作為6個數學核心能力之一，并將其定義為：“用某種形式，例如書面符號、圖形（表）、情景、操作性模型、文字（包括口頭文字）等，表達要學習的或處理的數學概念或關系，以便最終解決問題．”[9]PISA中對數學表征能力的定義在逐步更新和發展，但其在2018年評價框架中基本延用之前的定義，即“表征能力需要選擇、解釋、轉換和使用各種表征來捕獲情境的數學本質、解決問題或展示自己的作品”[8]．這里將數學表征能力界定為數學表征（包括符號表達、圖形圖表、操作模型和情境）之間的動態操作，以表達交流、操作轉換和建模應用各種表征來呈現、解決數學或現實問題．

1.2 分析框架

美國的《學校教育原則和標準》（2000）將數學表征能力按要求分為3個維度：第一，“創造和利用各種數學表征來組織、記錄和交流數學觀念”；第二，“選擇、應用和互換各種數學表征方法解決問題”；第三，“應用表征模擬并解釋物理的、社會的和數學中的現象”[7]．Niss[10]（2003）將數學表征作為八大數學能力之一，并列舉出3條表征數學實體（對象和情境）能力的要求：其一，理解和利用（解碼、解釋、區分）數學對象、現象和情境的不同種類的表征；其二，理解和利用同一實體的不同表征之間的關系，包括了解它們的相對優勢和局限性；其三，選擇和切換表征．PISA2018的數學評估框架依據3個數學過程對數學表征進行了維度劃分，即以數學方式表述情境，運用數學概念、事實、程序和推理，解釋、應用和評估數學結果[8]．

綜上，3者均將數學表征能力劃分為3個維度，美國的《學校教育原則和標準》（2000）與PISA2018的維度劃分有異曲同工之妙，而Niss的維度劃分與前兩者劃分有些不同，未明確提出應用的要求，但3者的要求均有在交叉維度中出現．為方便此次課程標準（教學大綱）幾何教學內容的文本分析，得出數學表征能力的分析框架如表1所示．此分析框架為三級：第一級為表征水平，將表征能力分為表達交流、操作轉換和建模應用3類；第二級為內涵，表達交流水平分為符號表達、圖形，操作轉換水平對應操作模型，建模應用水平對應情境應用；第三級為樣例，舉例說明其對應更為具體的數學表征，而且，將符號表達進一步界定為書面符號（文字），操作模型進一步分為公理（定理/性質）和計算（方法）．

表1 數學表征能力分析框架

1.3 研究對象

研究對象來源于《20世紀中國中學數學課程標準·教學大綱》中的中學部分課程標準或教學大綱、2001年和2011年出版的《義務教育數學課程標準》中的初中部分、以及2003年和2017年出版的《普通高中數學課程標準》．由于涉及的文本年限跨度較大，內容較多，這里將僅從平面幾何和立體幾何兩科目來探討數學表征能力在中學數學課程標準（教學大綱）對應教學內容模塊中的發展趨勢．為簡便起見，后文將課程標準或教學大綱簡寫為課標或大綱．

1.4 研究方法

采用文本分析法，其編碼流程分為3個階段，即初步形成編碼表—效度檢驗—使用編碼表及信度分析．第一階段：通過閱讀文獻確立3個表征水平指標及對應內涵，利用分析框架形成編碼表，兩個成員再分別選用相同的3個課標的幾何教學內容進行文本分析，在文本中尋找對應的關鍵詞，修正內涵，并進一步確定關鍵詞樣例，初步形成一致的編碼表和關鍵詞選取原則（根據分析框架的內涵和樣例選擇最合適的分類，其中若關鍵詞有多種含義，至多填入兩種樣例分類）．第二階段：第三個未參與的成員使用此編碼表隨機選取除之前選定的課標進行編碼，檢驗此編碼表的有效性，若有效則進入第二階段，否則進一步修正分析框架的第三級指標，二次編碼和驗證，直至有效．第三階段：第一作者使用編碼表對幾何各部分內容文本的關鍵詞進行檢索、分類、計數統計．請第三作者隨機選取3個課標，按照編碼表依次對平面幾何、立體幾何編碼表進行詞頻統計，匯總為高中和初中兩個階段，計算得到內部一致性分別為0.964和0.941．因此，編碼結果具有較高的信度和效度．

2 研究結果

20世紀的中學數學課程標準（教學大綱）是從1902年開始存在的．但是，從1923年起，中學數學課標才呈現具體的教學內容．因為依據上述分析框架對數學課標的教學內容模塊進行分析，所以接下來將僅呈現1923年之后的結果并予以分析．

2.1 平面幾何

2.1.1 初中

如圖1所示，從變化趨勢來看，表達交流水平和操作轉換水平波動較大，二者變換趨勢大體一致，均表現為逐漸上升，但建模應用水平波動很小；從數量上來看，操作轉換水平最多，表達交流水平次之，建模應用水平最少．

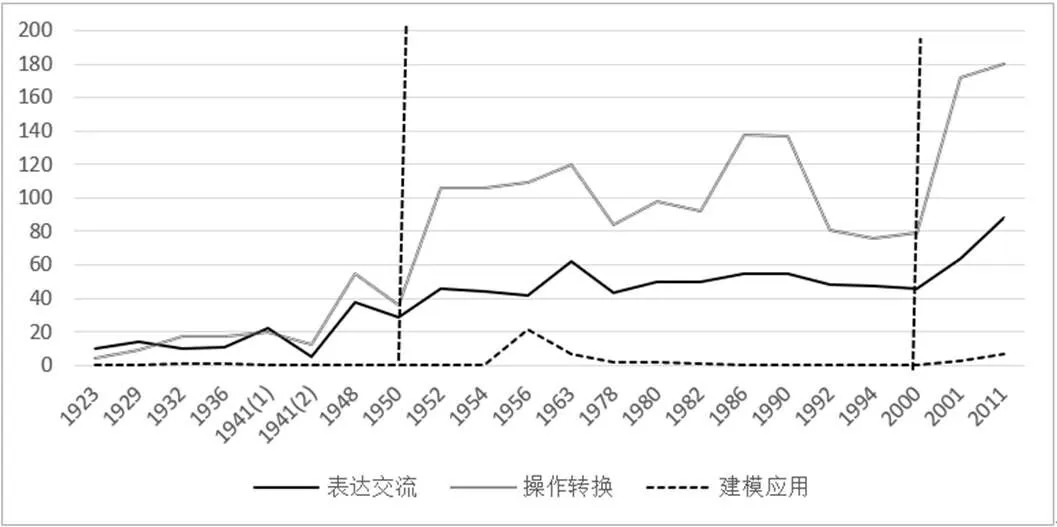
圖1 基于編碼的初中數學課標平面幾何教學內容

（1）第一階段（1923—1951）．

初始時期，由于課標剛剛加入具體教學內容，未進一步充實，所以課標教學內容的描述更加側重表達交流水平．1932年開始，課標增加了實驗幾何單元，同時強調幾何應注重直觀；并將“訓練學生關于計算及作圖之技能，養成計算純熟準確，作圖美潔精密之習慣”[11]列為課程目標之一．這些均體現了課標對于操作轉換水平的重視在不斷增加．抗戰勝利后，為適應社會需求，1948年教育部重新修訂課標，教學內容較之前更加具體．而新中國成立后，教育部通過座談會的方式發現數學教材編排不合理、學生負擔過重，并于1950年頒發了精簡綱要草案，精簡教材中不必要或重復的內容，故而知識數量降低．

課標雖然在教學內容模塊未有涉及建模應用水平，但其它模塊有體現相關內容．由于抗戰背景所致，實施方法均提出了關于軍事方面的具體應用，如測量、測繪等．而且教學目標也強調了數學與日常實際生活的聯系．

（2）第二階段（1952—2000）．

總體來說，課標的教學內容在適應中國國情的探索過程中逐步成熟．“52大綱”與中國之前的大綱相脫離，以蘇聯最新的十年制數學教學大綱為藍本，采取“先搬過來，再中國化”方針，只修改和補充完全不符合中國情況的內容，故大綱的教學內容數量和前面未能保持一致的趨勢．并且，該大綱注重系統地研究幾何圖形的性質，以解答計算題和作圖題，因此操作轉換水平大幅提升．學習蘇聯時期，3個大綱中的幾何教學要求都有提到要“運用所學知識解決實際問題”，但僅“56大綱”增加了一些有關生產技術的教學內容，與建模應用水平相對應．

1960年，教育部送呈的“關于修訂中、小學數學教學大綱和編寫中、小學數學通用教材的請示報告”指出，“根據中國和兄弟國家的教學經驗，初中學完平面幾何是可能的”[11]．相應地，從1963年開始，中國高中課標的平面幾何教學內容全部移入初中，因此該年大綱的教學內容大幅度提升．同時，其教學要求指明要掌握平面幾何的基礎知識，“解答平面幾何的證明題、計算題和作圖題，進行簡單的測量，以適應參加生產勞動和進一步學習高中數學、物理、化學等科的需要”[11]，這也對應著表征的3種水平．

1986年開始，為配合義務教育的實施，中國在頒發義務教育課標的過渡期以及實施階段，均秉承減負的理念．如1986年大綱針對1978年大綱的教學內容做了適度調整，遵循“適當降低難度，減輕學生負擔，教學要求盡量明確、具體”[12]的原則；1990年對“86大綱”的修訂說明指出“減去過多的內容，降低過高的要求”[11]．

（3）第三階段（2001至今）．

第三階段，處于新世紀課程改革時期，其主要特征為：與前一階段相比，由于教學內容和教學要求混編的呈現方式進一步細化了教學內容，表達交流水平和操作轉換水平均顯著增長．特別地，教學內容更多以操作要求的形式展現．而且，教學內容也加入了些許應用，建模應用水平有小幅增長．

“01課標”設置了“空間與圖形”以取代歐幾里得幾何體系．演繹幾何相對減少，實驗幾何大幅增加，尤其新增大量變換幾何內容，更多地與操作轉換水平相對應．雖然課標與實際生活聯系更加密切，要求從實例中探索、感受和認識圖形[13]，但其關于解決實際應用問題的要求還是最少，即教學內容較少強調建模應用水平．

相對于“01課標”，2011年版將“空間與圖形”改為“圖形與幾何”．而且教學內容仍在增多，其中，表達交流水平增長幅度最大．該課標從學生發展的角度出發，刪除了一些重復、脫離學生生活需要或學習有困難的內容，如梯形等；增加了相關內容的補充，如概念等進一步細化，對應的表達交流水平進一步凸顯[14]．同時，該課標也增加了與圖形證明相關的選學內容，以便為學生提供更多深入學習幾何的機會，操作轉換水平也相應增加．

2.1.2 高中

如圖2，從整體上看，高中平面幾何變化趨勢與初中不同，表達交流和操作轉換均呈下降趨勢，但操作轉換水平曾出現大幅增長的區間，波動更大．同時，與初中有所相似的地方是，除前兩個教學大綱之外，操作轉換水平的數量一直高于表達交流水平，而且建模應用水平一直數量最少，僅有小幅度波動．

（1）第一階段（1923—1949）．

該階段初期處于摸索階段，教學內容在不斷減少，從1932年開始趨于穩定．其主要特征體現為：隨著課標表述愈發簡潔，表達交流和操作轉換相應的教學內容在逐步下降的過程中趨于穩定，二者的變化折線也由緊密相鄰到逐漸分化．

圖2 基于編碼的高中數學課標平面幾何教學內容

此階段課標增加了大量知識，寫法卻較之前精簡，概念和定理少有進一步展開．但教法要求強調了幾何證明及作圖，這也可能導致操作轉換高于表達交流．1948年課標改動較多，刪減了作圖方法和部分定理，增加了部分圖形．建模應用水平在此階段體現很少．從1932年開始，提到了“基本軌跡及其應用”，可以作為建模應用水平的雛形；在抗日戰爭階段，教學要求增加了軍事應用，如作圖和測量等．

（2）第二階段（1950—2002）．

相比于第一階段，該階段的操作轉換水平和表達交流水平進一步出現明顯分化．同時，該階段出現一段平面幾何教學內容空白期（1963—1995）．

1950—1962年，操作轉換水平顯著高于交流表達．1950年精簡綱要對證明和作圖方法說明更加明確．與之前課標不同，經學習蘇聯后，大綱的知識單元劃分得更加細致．而且“56大綱”增加了與實地測繪有關的教學內容，建模應用水平有所體現．

1996年，作為現代數學內容的一部分，平面向量首次列入中國高中大綱，這也一定程度上說明了中國中學數學在不斷地向現代化發展[15]．或許由于平面向量剛剛引入，大綱還未提及建模應用，僅有“向量”和“向量的坐標表示”與表達交流水平對應，其余均為操作轉換水平．這也可能是由于向量是幾何轉為代數的工具，除用于表示幾何之外，更加注重工具性的使用．

（3）第三階段（2003至今）．

此階段課標教學內容與20世紀末保持一致，仍只有平面向量，但較之前，表達交流水平和操作轉換水平都有不同程度的增長．后者內容多于前者，與“增加數學意識”的要求有一定關系[16]．同時，建模應用水平對應的教學內容再次出現，這也體現著高中數學課程標準制定組重視數學運用意識[17]．

2017年版課標與“03課標”的向量內容基本一致，雖然向量的概念及表示在“加細”說明，但由于向量本身的工具性，教學內容對其操作轉換描述更多．值得一提的是，向量應用作為單獨課時，尤其提到用以解決力學問題．

2.2 立體幾何

2.2.1 初中

如圖3所示，從1932年起，初中課標才有滲透少量的立體幾何內容．其中，除1948年外，表達交流水平一直存在于各時期課標教學內容中，相比之下，操作轉換水平對應的教學內容在1963—2000年出現空白期；而建模應用水平在新世紀課標中才有體現．

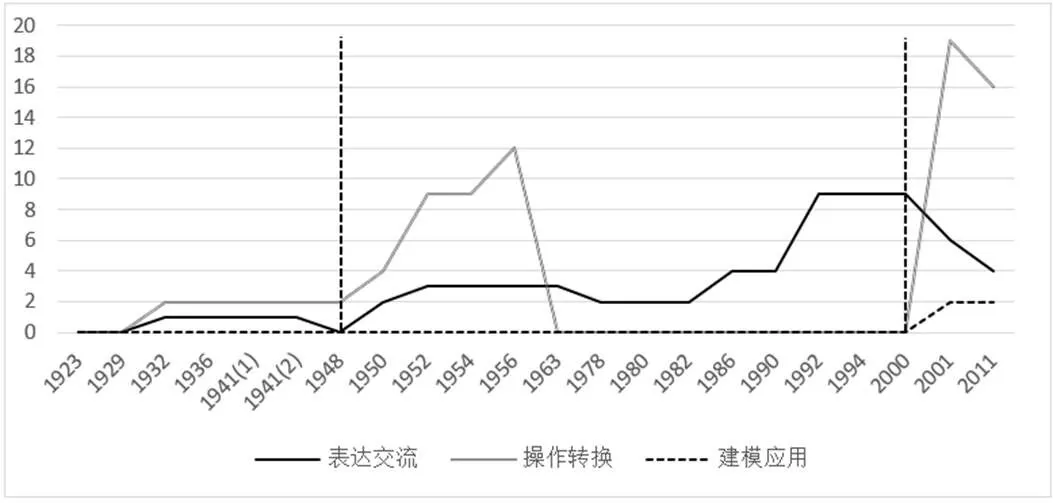
圖3 基于編碼的初中數學課標立體幾何教學內容

（1）第一階段（1923—1949）．

初中課標的立體幾何僅體現在實驗幾何中，包含“空間幾何圖形”和“立體面積及體積之度量”，分別對應表達交流水平中的1項圖形和操作轉換水平中的2項計算；而抗戰勝利后，1948年修訂的課標僅剩余“簡易立體面積及體積之計算”．

（2）第二階段（1950—2000）．

與前一階段相比，表達交流和操作轉換水平的平衡狀態被打破，均出現明顯增長．1950—1956大綱中，實驗幾何內容被包含在算術學科，立體幾何集中于“體”、“面”和“簡單幾何體”的體積計算公式．學習蘇聯大綱時期，課標又加入了幾個簡單幾何體的表面積．除此之外，“56大綱”進一步要求制作包括立方體和長方體模型以及對應的展開圖，與該大綱的算術課程中的幾何教學方法提到的“利用圖形、模型和常見的物理，讓學生直觀地認識各種幾何圖形”[11]相

呼應．

1963—2000年，初中課標僅包含表達交流水平．1963年起，初中算術課程取消，只講授平面幾何內容，該大綱僅在幾何緒論中出現“體”和“面”與立體幾何對應．而從1978年開始，教學要求新增“初步了解簡單體的視圖”[11]，注重培養學生的空間想象能力，與之對應的教學內容為“視圖的初步知識”和“簡單體的視圖”[11]，并刪去了幾何緒論．“86大綱”又增加了“二視圖”和“三視圖”，進一步擴充了知識內容．1992年起，中國正式啟用《九年義務教育全日制初級中學數學教學大綱（試用）》，發展學生的空間觀念在該大綱中體現更加突出，分布在幾何緒論、空間直線、平面的位置關系和視圖3個部分．

（3）第三階段（2001至今）．

“01課標”中，立體幾何的教學內容集中分布于視圖與投影．由于教學內容與具體要求混編，“視圖”內容改為從操作的角度敘述，故而操作轉換劇烈增長，表達交流相應減少．當然，這也可能與該課標幾何體系發生改變，突出空間觀念有關．2011年延續前一課標，將之前的“視圖與投影”改為“圖形的投影”，三視圖的要求未變，刪除了陰影、視點、視角盲區等內容，故而表達交流再次下降．但兩課標的建模應用水平均體現了基本幾何體的視圖與展開圖在現實生活中的應用．

2.2.2 高中

如圖4所示，從變化趨勢來看，操作轉換水平波動最大，波峰波谷較多；相比之下，表達交流水平波動較單一，總體趨勢為先上升后下降；建模應用水平僅有3次近乎與零刻度線貼合的波動．從數量來看，建國前，除個別課標外，表達交流水平對應的教學內容均高于操作轉換水平，建國后，恰好相反；建模應用水平數量接近于零．

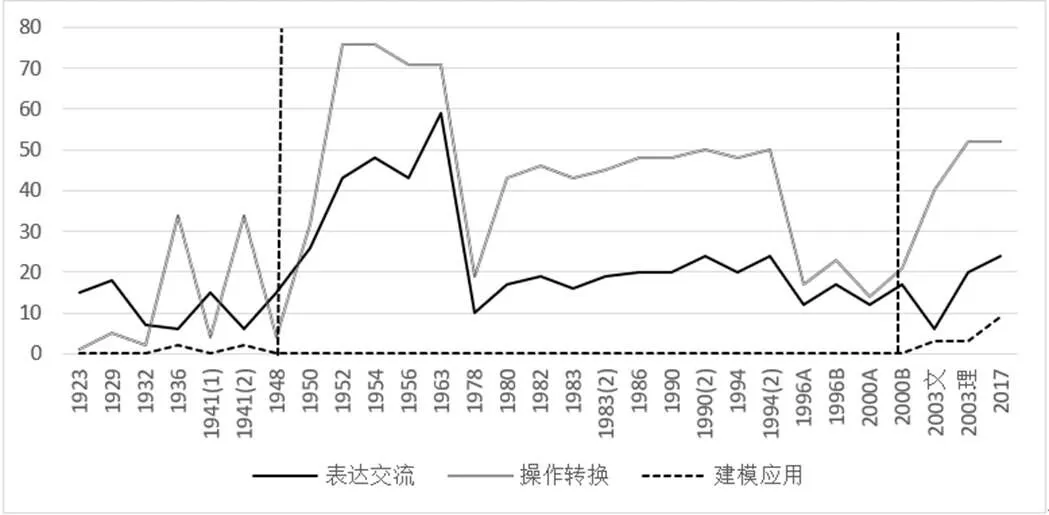
圖4 基于編碼的高中數學課標立體幾何教學內容

（1）第一階段（1923—1949）．

在1923年和1929年的課標教學內容中，立體幾何在幾何“空間部”單元呈現．1932年課標教學內容首次出現“立體幾何”字樣．此3個課標的教學內容全部以羅列圖形為主，計算和定理次之，未涉及應用．特別地，1932年公布的正式課標增加了代數和三角部分的內容和課時，而幾何課時每周減少一次，立體幾何較之前刪除了空間位似圖和空間對稱圖等內容．

1941年六年制課標與1936年課標基本保持一致，區別是1936年課標為緩解學生學業壓力，提出分兩組方案教學，僅甲組包含立體幾何，而1941年不再分組教學．兩課標的立體幾何教法要點均提出需注重空間性質及量法，因此偏重操作轉換水平．而且，其教學內容包含“關于多面體及回轉體之各種應用問題”，與建模應用水平相對應．

為適應抗戰需求，1941年修訂的高中課標，該立體幾何課時每周縮短一小時，降低了對其教學要求，而且教法要點提出“使學生能將空間圖形表示清楚”[11]，突出了對表達交流水平的需求．可能與初中算術中已講授立體面積與體積有關，高中課標的求積計算只包含球．抗戰勝利后，1948年修訂課標與1941年修訂課標在立體幾何教學內容保持一致，僅提高了教學要求．

（2）第二階段（1950—2002）．

與第一階段相比，該階段課標操作轉換水平持續高于表達轉換水平，未提及建模應用水平，但在教學目的均提及到與實際相聯系．

從1950年開始，中國課標的教學內容對許多綱目進一步細化，圖形和定理、面積與體積的計算數量均在增多，且后者比重稍多于前者．學習蘇聯時期，大綱均在說明模塊中清晰地指出了幾何的教學目的，對幾何圖形性質的系統研究和面積、體積的計算，對學生邏輯思維和空間想象能力的培養以及幾何的實際應用與測量．與此對應的，教學內容除了包含直線與平面、多面體和回轉體等立體圖形外，性質、定理、求積運算等內容要遠高于之前課標．

“63大綱”強調了基礎知識和基本技能的重要性，而且立體幾何的教學內容增加了多面體和旋轉體的直觀圖、二視圖等圖形．“78大綱”中，直線和平面在空間的位置關系相關內容未有縮減，但對多面體和旋轉體的要求僅剩“能解決有關柱、錐、臺、球的一些計算問題”，教學內容未有進一步呈現，所以表達交流水平和操作轉換水平這些都跌至前面的最低點．

1978—1995年，立體幾何教學內容在各數學表征能力水平變化穩定．“80大綱”是在“78大綱”的基礎上修訂的，除了多面體和旋轉體計算有進一步擴展外，部分幾何體的概念、性質、畫法也被列入，因此表達交流水平和操作轉換水平都有增加．1996—2002年課標教學內容3個水平的分布保持一致．與之前大綱的區別在于教學內容再次精簡，如幾何體的表面積和體積計算只呈現在具體要求中．

（3）第三階段（2003至今）．

新世紀課程改革開始，課標教學內容與教學要求混編，很多關鍵詞由原來的靜態轉為動態，操作轉換水平顯著提升．2003年高中課標實行文理科不同教學內容，理科較文科多出“空間向量與立體幾何”單元．而且，從2003年開始，建模應用水平對應的教學內容再次出現，如2003年課標的實習作業要求畫建筑物的直觀圖和三視圖，2017版課標有對幾何體表面積和體積公式的實際應用等．

3 討論與結論及啟示

從平面幾何、立體幾何課程教學內容模塊，對20世紀以來中國中學數學課程標準（教學大綱）中數學表征能力趨勢進行梳理，可以初步得到以下結論．

（1）中國中學課標對數學表征能力的表達交流水平和操作轉換水平一直比較注重，特別地，對于操作轉換水平的關注一直處于增加的過程，而對表達交流水平的要求相對穩定．

（2）21世紀以前的數學課程標準（大綱）較少關注數學表征能力的建模應用水平，新世紀以后的課程標準在這方面有一定增長，尤其是2017年版高中課標將數學建模活動與數學探究活動單獨作為一個主題．因此，與建模應用相關的數學表征能力將會受到越來越多的重視．

研究還發現，上述結果與時代背景密切相關，其知識內容及體系在不斷適應社會和個人發展的過程中變化著．

20世紀50年代，中國教育開始進入全面學習蘇聯階段，將蘇聯十年制學校數學教學大綱改編為中國新大綱．該大綱教學內容的結構較中國之前大綱更加嚴謹，著重了對知識與技能的系統學習和邏輯思維的訓練，因此，數學表征能力主要體現在操作轉換和表達交流上．

20世紀80年代，隨著改革開放時期的到來，中國的教育開始全面進入復蘇和發展階段．課標的修訂過程立足于中國的國情，在實踐中不斷吸取經驗[18]．課標更加強調基礎知識和基本技能．而且，為減負，課標推出因材施教，分科教學或增加選學內容模塊，有益于學生的個性發展．

為適應新世紀的迅速發展，中國先后分別頒發了兩次《義務教育數學課程標準》和《普通高中數學課程標準》．隨著許多國家將數學表征能力列為學生的數學關鍵能力之一，數學表征能力在中國課標中也愈發得到重視，并且一直呈現增長趨勢．特別地，建模應用水平在課標的教學內容中一直體現較少，但2017年版高中課標將數學建模活動和數學探究活動作為4個主題之一．這一舉措展現了課標對建模應用的重視程度以及單獨發展中學生建模能力的必要性．目前，新的義務教育數學課標修訂在即，建模活動也很大程度上適合被增入新修訂的課標中．

通過研究，可以得到如下啟示：（1）在許多國家的中學數學課程標準和數學表征能力的相關文獻中，數學表征能力被列為學生數學核心能力之一，因此中國中學數學課程標準也應對數學表征能力的內涵、行為表現提出明確的要求；（2）強調“雙基”教學是中國數學課程的傳統，在保持傳統的同時，應該大力提倡數學應用、數學探究和數學建模活動，特別是即將修訂的義務教育數學課程標準，也需提出明確的課程及教學要求．

致謝：特此感謝華東師范大學教師教育學院徐斌艷教授、數學科學學院范良火教授和鮑建生教授在文章寫作過程中給予的指導和幫助．

[1] 周華．數學表征在初中課堂中的教學與思考[J]．數學教學通訊，2017（32）：67-68．

[2] 唐劍嵐．國外關于數學學習中多元外在表征的研究述評[J]．數學教育學報，2008，17（1）：30-34．

[3] 孫雪梅，趙永香，朱維宗，等．云南民族地區六年級彝族學生數學問題解決表征水平的調查研究[J]．數學教育學報，2016，25（3）：85-92．

[4] 張晉宇，姜慧慧，謝海燕．數學表征與變換能力的評價指標體系研究綜述[J]．全球教育展望，2016，45（11）：13-21．

[5] 夏征農，陳至立．辭海[M]．6版彩圖本．上海：上海辭書出版社，2009：161．

[6] LERMAN S. Encyclopedia of mathematics education [M]. Dordrecht: Springer Netherlands, 2014: 409.

[7] 全美數學教師理事會．美國學校數學教育的原則和標準[M]．蔡金法，譯．北京：人民教育出版社，2004：65．

[8] OECD. PISA for development assessment and analytical framework: Reading, mathematics and science [M]. Paris: OECD Publishing, 2018: 56.

[9] 徐斌艷．數學學科核心能力研究[J]．全球教育展望，2013，42（6）：67-74．

[10]??NISS M. Mathematical competencies and the learning of mathematics: The Danish KOM project [C]. 3rd Mediterranean conference on mathematical education, 2003: 115-124.

[11] 課程教材研究所．20世紀中國中小學課程標準·教學大綱匯編（數學卷）[M]．北京：人民教育出版社，1999：228，264，428，400，434，456，461，578．

[12] 中國教育年鑒編輯部．中國教育年鑒（1988）[M]．北京：人民教育出版社，1989：334．

[13] 孔凡哲，劉曉玫，孫曉天．《義務教育階段國家數學課程標準》“空間與圖形”的特點[J]．數學教育學報，2001，10（3）：58-61．

[14] 史寧中，馬云鵬，劉曉玫．義務教育數學課程標準修訂過程與主要內容[J]．課程·教材·教法，2012，32（3）：50-56．

[15] 呂世虎．中國當代中學數學課程發展的歷程與啟示[D]．長春：東北師范大學，2009：5．

[16] 陳重穆，曾崇燊，宋乃慶．從素質教育看21世紀的高中數學課程[J]．課程·教材·教法，1995，15（9）：40-42．

[17] 《國家高中數學課程標準》制訂組．《高中數學課程標準》的框架設想[J]．數學教育學報，2002，11（2）：1-7．

[18] 夏明德，顧泠沅．面向實際不斷修訂[J]．數學通報，1982，21（7）：1-3．

The Development Trend and Enlightenment of Mathematical Representational Competency in Mathematics Standards of Middle School in China since the 20th Century——Taking Geometry as an Example

LI Na1, ZHANG Jin-yu2, 3, SHEN Yang1

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. College of Teacher Education, East China Normal University, Shanghai 200062, China;3. Shanghai Research Base for School Mathematics Education, Shanghai 200241, China)

According to the Chinese mathematics syllabi of middle school in different eras since the 20th century, the paper used text analysis method to construct an analytical framework of mathematical representational competency based on related research, which contained three levels, i.e. (1) expression and communication, (2) operation and transformation, and (3) modelling and application. Based on the framework, we then analyzed the content of plane geometry and solid geometry in Chinese mathematics syllabi for middle school respectively, and further discussed the developmental trend of the competency in Chinese middle school mathematics syllabi since the 20th century and the enlightenment. The results showed that Chinese middle school mathematics syllabi gradually paid more attention to operation and transformation, whereas the request for expression and communication remained relatively stable. Compared with them, the syllabi showed less attention to the modelling and application, though the situation was slightly better than before.

mathematical representational competency; mathematics in middle school; syllabus; course content; geometry

2019–03–16

教育部人文社會科學重點研究基地重大項目——中國學生數學素養測評研究（16JJD880023）；上海高校“立德樹人”人文社會科學重點研究基地——華東師范大學數學教育教學研究基地項目（A8）

李娜（1994—），女，遼寧遼陽人，博士生，主要從事數學教育研究．

G423.07

A

1004–9894（2019）03–0036–06

李娜，張晉宇，沈陽．20世紀以來中國中學數學課程中數學表征能力的發展趨勢與啟示——以幾何為例[J]．數學教育學報，2019，28（3）：36-41．

[責任編校：周學智、陳雋]