初中數學學業評價與課程標準的一致性研究——以福建省五套中考數學試卷為例

徐 帆，張勝元，孫慶括

?

初中數學學業評價與課程標準的一致性研究——以福建省五套中考數學試卷為例

徐 帆1，張勝元2，孫慶括3

（1．江西省贛州市第三中學，江西 贛州 341000；2．福建師范大學 數學與信息學院，福建 福州 350117；3．南昌師范學院 數學與計算機科學系，江西 南昌 330032）

學業評價與課程標準的一致性問題不容忽視．福建省5套中考數學試卷與課程標準的一致性水平側重不一：各維度一致性結果整體較好，各領域一致性水平不盡相同．產生的原因可能是：與國家課程標準中存在的不足有關，與命題專家關注度不夠有關，與教師一致性素養不高有關，以及研究工具自身的不足有關．提高試卷與課程標準吻合程度的途徑有：進一步完善課程標準，命題基于一致性視角，教學實踐融入一致性，研制本土一致性工具．

課程標準；學業評價；一致性；韋伯分析模式

1 前言

中國于21世紀初進行了新一輪國家基礎教育課程改革，頒布了《基礎教育課程改革綱要（試行）》（簡稱《綱要》），2001年頒布了國家課程標準，這為國內一致性研究提供了孕育的土壤．需要指出的是，此次“新課改”的本質就是基于課程標準的改革．《綱要》明確規定：“國家課程標準是教材編寫、教學、評估和考試命題的依據，是國家管理和評價課程的基礎．”[1]進一步，初中學業評價（簡稱中考）作為義務教育階段的終結性測驗，兼具“畢業性”和“選拔性”雙重性質，對促進中等教育發展、人才培養和選拔至關重要．2011年頒布的《義務教育數學課程標準》[2]（簡稱《課程標準》）作為一個綱領性文件，也是中考試卷命制的根本依據．因此，確保學業評價與課程標準的一致性，才能有效檢測學生應有的認知水平和應具備的技能水準，才能有效發揮學業評價所承載的選拔功能，所以學業評價與課程標準的一致性問題不容忽視．

2 文獻述評

回顧國內外學業評價的一致性研究現狀，美國在其中擔任重要角色．一致性研究始于美國，成熟于美國．20世紀60年代中期，美國各州應聯邦教育部要求，陸續使用國家常模測試，但由于測試之初經驗匱乏，忽視了測試與美國州立課程標準之間的匹配度，因而導致測試不足以體現學生應有的認知水平和技能水準．基于此，學業評價與課程標準是否具有一致性才進入人們的視野．1980年代初，美國掀起了一場“基于標準的教育改革運動”，此次改革制訂了一項檢測州立學校是否有效落實課程標準的關鍵性指標．此時研制一致性分析模式成為美國基礎教育課程研究領域的重要課題[3]．至90年代，美國教育部頒布了多個改革文件，進一步使課程標準在學業評價中占據核心地位．進入21世紀，美國教育部2001年《不讓一個孩子掉隊》法案的成功實施，把一致性研究推向了新的高度，它進一步確定了評價對于學科學習內容的重要性，并規定用一致性分析來檢測課程標準的實施情況．

國內一致性研究起步較晚，新課改時期頒布的課程標準可視為孕育階段．通過中國知網（CNKI）檢索已有相關文獻，通過梳理可分為兩個階段．

第一階段為2011年以前，主要是國內學者對美國一致性研究的緣由、模式探索、研究范式進行歸納總結，并思考將其引入中國的可行性及需要面對的挑戰，最后得出結論研究模式需要本土化改造用于國內研究．這一階段較早的研究者有劉學智[4-6]、崔允漷[7]、范立雙[8]、張雷[9]、楊玉琴[10]、岳喜騰[11]等．其中劉學智是國內最早進行一致性研究的學者之一，他發表的多篇文章對國內一致性研究提供了很好的理論支撐，也對國內一致性研究起到很好的推動和傳播作用．

第二階段為2011—2018年，主要是國內學者借鑒美國一致性研究模式在國內進行各科定量分析．通過中國知網檢索，其中以“課程標準一致性”為主題詞的文章涉及944篇，以“課程標準+一致性+數學”為主題詞的文章共有144篇文章，特別是以“中考+數學+一致性”的文章甚少，僅有7篇，研究模式多是SEC模式，專門針對韋伯模式的中考試題研究僅有3篇相關論文，可見目前中考數學學科在這方面的研究還有待進一步加強．

綜上所述，盡管目前中國在一致性領域研究取得長足進步，但還存在一致性量化研究不足、對中考的一致性關注度不夠等現象．基于此，研究者以福建省中考數學試題為例探析試卷的一致性，以期檢測試卷與課程標準的吻合程度，更好地幫助教師理解課程標準、學業評價和課堂教學3者之間的聯系，最大程度地利用課程標準來指導教學實踐．

3 研究設計

3.1 研究對象

2011年頒布的課程標準；2017年福建省統一中考數學卷（編碼“A”）；2016年福州市中考數學卷（編碼“B”）；2016年廈門市中考數學卷（編碼“C”）；2016年龍巖市中考數學卷（編碼“D”）；2016年南平市中考數學卷（編碼“E”）．

3.2 研究工具

通過比較目前主流的一致性研究工具韋伯分析模式、SEC分析模式、Achieve分析模式，最后采用韋伯分析模式，它具有研究維度更全面、程度更精細、操作更簡便、臨界值更明確等優勢．它是1993年諾曼·韋伯（Norman L. Webb）博士在美國國家科學發展基金會（NSF）和美國州的合作項目（SCASS）的資助下，開發的學業評價與課程標準的一致性工具，作為一致性研究面世的第一個研究工具，它在美國各州得到廣泛運用并得到美國多個行政部門的高度評價，在國內也有較好的適應性．

韋伯認為要進行一致性分析，首先要對課程標準中的內容目標進行描述，即構建“金字塔”式課程內容目標體系，頂端為“學習領域”，中部為學習領域下設的“學習主題”，最下層為學習領域的“具體目標”[12]．進一步，韋伯認為在教育領域，一致性研究主要表現為5個維度，即情感態度維度、知識技能維度、認知要求維度、教育公平維度和教學維度，而“韋伯分析模式”主要是從“知識技能”和“認知要求”兩個維度考量試卷與課程標準的一致性，又分為“知識種類”“知識深度”“知識廣度”“知識分布平衡性”4個子維度判斷一致性[3]．具體的韋伯一致性判斷標準如表1．

表1 韋伯一致性可接受水平判斷標準[13]

3.3 研究過程

3.3.1 本土化改造

目前中國大部分一致性研究都直接采納和編譯國外一致性工具，自編工具較少．很顯然，國外現有工具由于文化差異、教育理念的不同以及課程重點等因素會導致直接編譯的工具不能很好地反映中國實情[14]．因此，研究者在借鑒美國韋伯分析模式進行一致性研究時，不能按部就班地直接套用于中國，而應該基于此模式進行適度本土化改造．

第一，知識深度水平本土化．韋伯分析模式的知識深度水平劃分為4個等級，分別是“回憶”“技能（概念）”“策略性思維”“拓展性思維”，考慮到兩國課程標準的差異性，按中國課程標準中的結果性目標進行編碼，對應的知識深度水平劃分為“了解”“理解”“掌握”“運用”．

第二，課程標準目標層次本土化．按照中國課程標準內容編排的特點，把韋伯“金字塔”式目標體系劃分的3個層次本土化改造為4個層次目標，即學習模塊、學習領域、學習主題、具體目標，如圖1所示．另外，4個學習模塊“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”共分為9個學習領域[2]．其中“統計與概率”模塊具體分為“抽樣與數據分析”“事件的概率”兩個學習主題，且內容不多，因此研究者把它合并為“統計與概率”學習領域．此外“綜合與實踐”是在其它3個模塊中加以具體落實．所以從“數與式”“方程與不等式”“函數”“圖形的性質”“圖形的變換”“圖形與坐標”“統計與概率”這7個領域分析一致性．

圖1 課程標準內容目標體系

3.3.2 編碼標準的確定

對課程標準進行編碼．首先，對學習模塊數與代數、圖形與幾何、統計與概率分別編碼1、2、3．其次，對模塊下設7個領域，分別編碼1.1、1.2、1.3、2.1……最后，對主題和具體目標依次編碼．例如，“圖形與幾何”模塊的學習領域有“圖形的性質”“圖形的變換”“圖形與坐標”，分別編碼2.1、2.2、2.3，圖形的性質領域下又分為“點、線、面、角”“相交線與平行線”等多個主題，依次編碼2.1.1、2.1.2……進而具體目標編碼為2.1.1.1、2.1.1.2……此外，對于課程內容中的單獨一條目標，有不同的行為動詞，要進一步拆分進行編碼．例如，“三角形”主題下的一條具體目標“理解三角形及其內角、外角、中線、高線、角平分線等概念，了解三角形的穩定性”，理解和了解是兩個不同的行為動詞，所以編碼時把它拆為“2.1.3.1理解三角形及其內角、外角、中線、高線、角平分線等概念”和“2.1.3.2了解三角形的穩定性”．最后，按照上述課程標準的編碼原則，把課程標準中的具體目標共編碼為219個．

對中考試題進行拆分編碼，然后按照課程標準的具體目標編碼表比對查找對應的編碼數據．例如，2017年福建省中考數學卷第11題計算，按照編碼標準分析，本題涉及3個知識點，分別為有理數的絕對值、零指數冪、有理數的混合計算，對應的課程標準具體目標編碼分別為1.1.1.5、1.1.1.8、1.1.4.1，最后把試題編碼數據填入試卷多項目表中，統計編碼數據后以表1的判斷標準確定是否符合課程標準的一致性．

4 研究結果

4.1 總體一致性分析

按照上述編碼原則，結合韋伯模式判斷標準，把編碼數據整理后得到表2．可見，在維度劃分上，5套試卷整體在知識分布平衡性維度的匹配程度最好，除了南平卷的“圖形與坐標”領域一致性稍差，5套試卷的其它領域都表現出一致性．其次，在領域劃分上，方程與不等式與課程標準的吻合程度最好，數與式、圖形的性質和統計與概率等3個領域的一致性結果也較好，但圖形與坐標領域一致性較差，它在“知識種類”和“知識廣度”兩個維度均不具有一致性．整體上，5套試卷與課程標準在“知識種類”“知識深度”“知識分布平衡性”3個維度與課程標準的一致性較好，而“知識廣度”一致性不盡人意，這也說明5套試卷所考查的知識面較窄，這與課程標準要求學生掌握的知識范圍出現嚴重偏差．

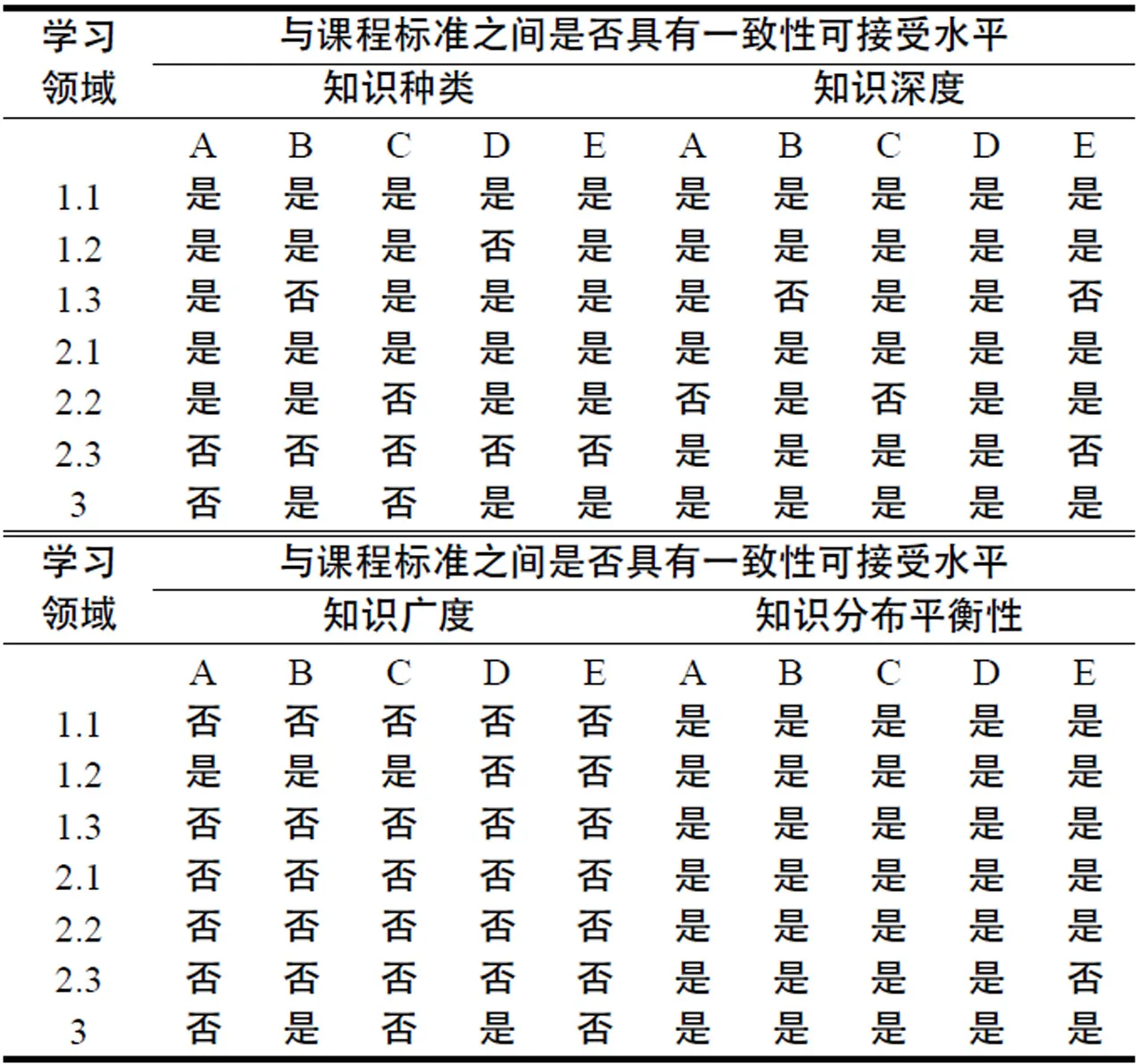
表2 福建省5套中考試卷與課程標準的一致性結果統計

注：根據編碼標準，編碼1.1表示“數與式”，1.2“方程與不等式”，1.3“函數”，2.1“圖形的性質”，2.2“圖形的變化”，2.3“圖形與坐標”，3“統計與概率”．A為2017福建統一卷，B為2016年福州卷，C為2016年廈門卷，D為2016年龍巖卷，E為2016年南平卷．

4.2 各維度一致性分析

4.2.1 知識種類一致性

5套試卷在圖形的性質領域與課程標準的一致性最好（如圖2），其最低擊中16個具體目標數，遠大于6個臨界水平．其次，數與式、方程與不等式、函數、圖形的變化4個領域結果也較好，而統計與概率則有兩套試卷擊中少于6個，這與課程標準的一致性表現稍差．特別地，圖形與坐標領域擊中量均小于6個，其最多擊中也僅為3道，特別是2016年南平卷在此領域擊中量為0．值得強調的是，5套試卷在函數領域擊中題量出入較大，其中廈門卷、南平卷和龍巖卷擊中較多，福州卷僅擊中3個目標，這與課程標準不具備知識種類一致性，但是函數在初中教學中的地位不言而喻，其本質、內涵和外延也是學生應掌握的內容，現階段中國提倡發展學生的核心素養，而函數在培養學生“數學抽象”“邏輯推理”“數學建模”等素養上占有舉足輕重的地位，理應得到重視．

圖2 5套試卷知識種類一致性分析

4.2.2 知識深度一致性

圖3是5套試卷在知識深度維度的一致性結果分布情況．若具有一致性用“1”表示，反之則用“-1”表示．5套試卷大部分領域都符合課程標準對知識的認知要求，表現出較好的知識深度一致性，也說明福建省內各試卷對學生應掌握知識的深度水平把控較好．但不容忽視的是，函數和圖形的變化領域均有2套試題不符合課程標準的認知要求．研究者通過對試題認知水平分析得知，造成結果的原因是多方面的．一方面，這兩個領域內容一般在試卷壓軸題出現，難度較大，從而導致考查高于課程標準的認知要求．另一方面，這兩個領域在各自模塊都是較為核心的內容，能夠較好融入其它知識點考查，以凸顯試卷的綜合性，但考慮到中考也應具有一定的選拔性，因此這兩個領域考查高于課程標準的認知要求也在情理之中，這樣有利于實現中考的選拔功能．

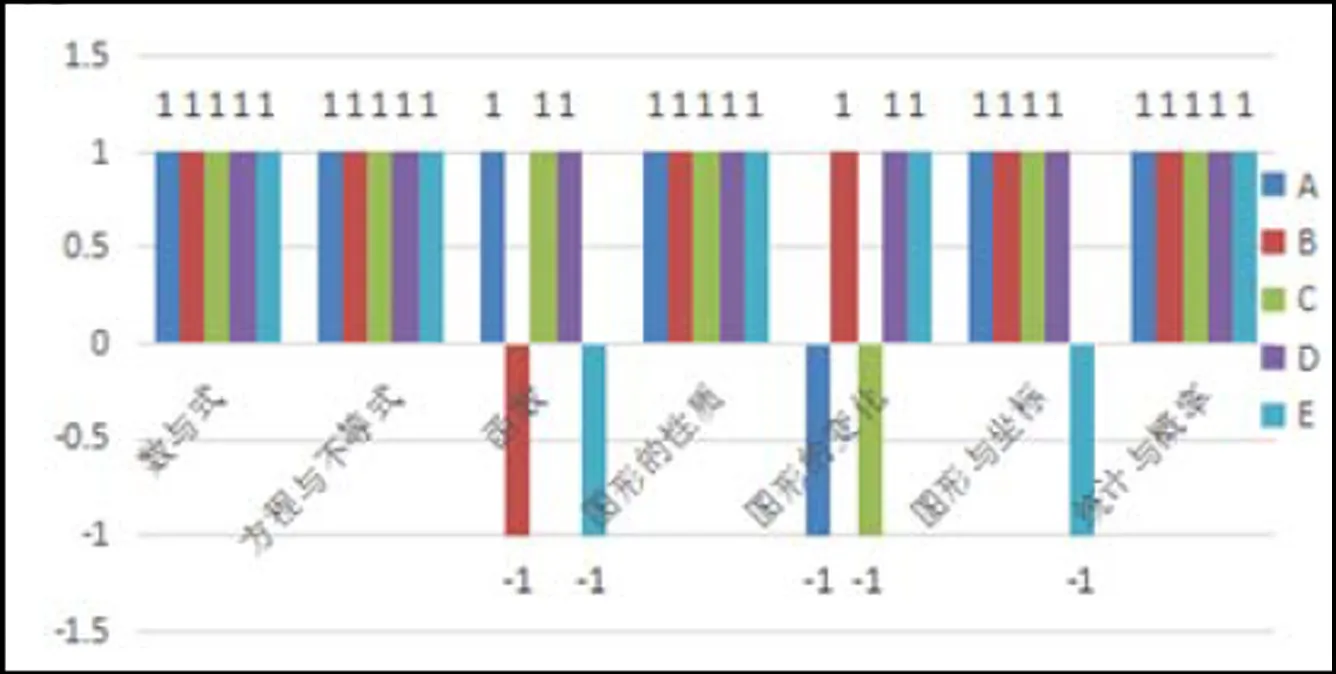
圖3 5套試卷知識深度一致性分析

4.2.3 知識廣度一致性

圖4是5套試卷的知識廣度一致性比值．按韋伯模式的判斷標準比值不低于50%定義可接受水平時，這5套試卷的一致性結果都不盡人意，但考慮到中考受考試形式與答題時間的限制，試卷對知識的考查不可能面面俱到，故知識廣度很難達到較高的百分比，于是研究者在考慮實際教育狀況的基礎上，以知識廣度比值不低于40%定義為可接受水平．但即使以此標準統計數據，也僅有部分試卷在“方程與不等式”和“統計與概率”領域達到一致性可接受水平．

進一步，研究者在對課程標準編碼過程中也發現其中存在諸多不足，這或許也是造成知識廣度一致性較差的原因．第一，課程標準中確實存在某些不合時宜的目標，例如“會用計算器求平方根和立方根”“能用計算器處理較為復雜的數據”等，但現在大部分地市中考已經明文規定不能使用計算器，所以這類目標也就得不到應有考查．第二，有些目標屬于學習過程中的階段性目標，但中考考查的知識較綜合，例如“能畫出反比例函數的圖像”“會用描點法畫出二次函數的圖像”等．第三，有些目標表達較模糊，這導致在試卷中難以體現，例如“經歷估計方程解的過程”“體會抽樣的必要性”等．

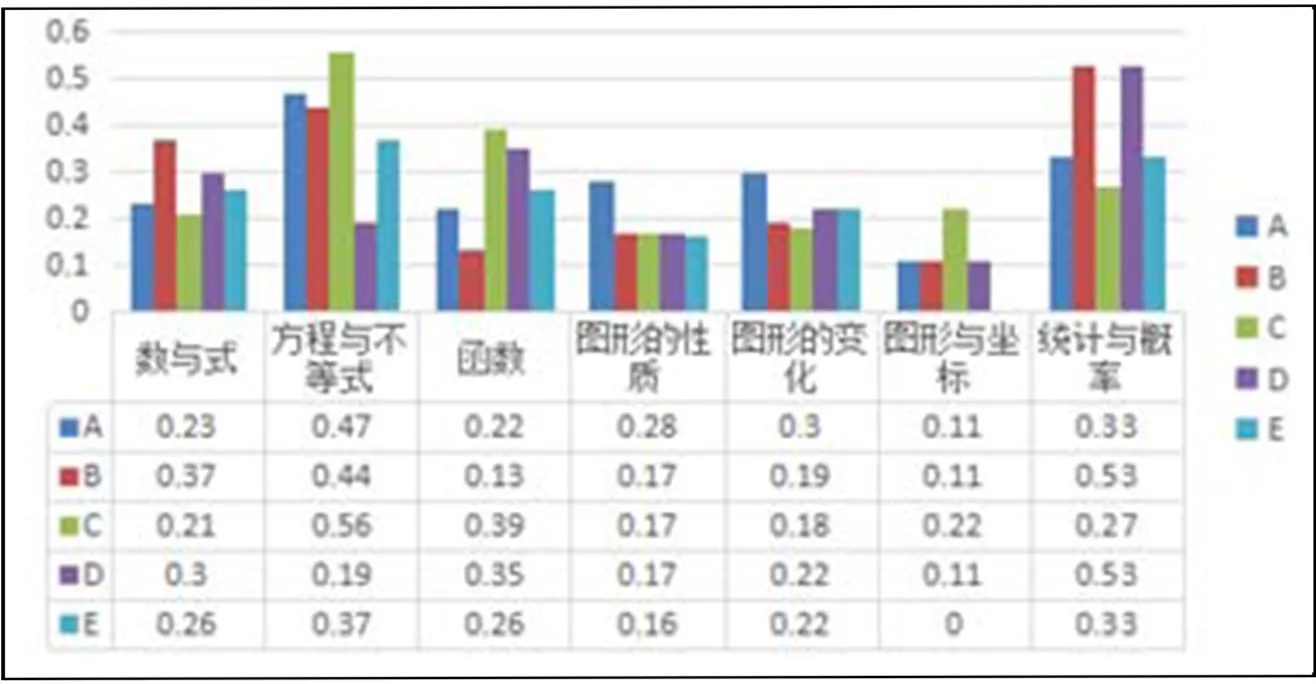
圖4 5套試卷知識廣度一致性分析

4.2.4 知識分布平衡性一致性

5套試卷除了在南平卷的圖形與坐標領域分布平衡指數為0外，在其它領域的分布平衡指數均大于0.7（如圖5），即在該維度與課程標準的一致性結果都很好，這也說明5套試卷在擊中目標的分布上是較均勻的，不存在明顯的目標集中堆積現象，可以有效地測驗學生對知識的整體把握情況．另外，知識分布平衡指數受該領域擊中具體目標試題數量影響，擊中試題越多則平衡指數信度就越高，研究也就更具價值．進一步，在采用韋伯模式驗證知識分布平衡一致性時，以試題擊中的“學習主題”進行分布平衡性分析，得到的結果與上文又有所差異．如對2017年福建卷按照試題擊中的“學習主題”進行分布平衡性分析，得到7個領域擊中的具體目標在主題下的平衡指數依次為0.680、0.875、1.000、0.690、0.875、1.000、0.700，可見，雖然2017年福建卷在各個領域下擊中的具體目標分布較為均勻，但在“數與式”“圖形的性質”領域主題下知識點的分布情況都不太好，當然這也說明試卷對各個主題的考查側重不一．

圖5 5套試卷知識分布平衡一致性分析

5 結論及思考

5.1 結論

研究結果表明，5套試卷與課程標準的一致性水平側重不一．首先，各維度一致性結果整體較好．知識種類、知識深度和知識分布平衡性這3個維度與課程標準的一致性要求基本吻合，但在知識廣度維度一致性不約而同地讓人失望，這與課程標準要求學生應掌握的知識范圍存在較大偏差．其次，各領域一致性水平不盡相同．“方程與不等式”“數與式”“圖形的性質”“統計與概率”4個領域一致性結果較好，其它3個領域一致性相對較差．

5.2 思考

5套試卷與課程標準的匹配程度并非十全十美，其中還存在一些知識偏離現象，或遺漏課程標準的一些核心內容，或高于課程標準的知識水平，可能導致學業評價無法實現其反饋功能，進而影響下一步的教學實施及高一級學校選拔優秀人才．究其原因是多方面的．

第一，可能與國家課程標準中存在的不足有關．表現型評價缺失，雖然課程標準內容中存在對學生學業評價的宏觀建議，但對學生學習后的表現評價還是缺乏具體的標準．中國課程標準還只是“看似一個缺少學習成果評價標準的課程內容框架”．另外，有些具體目標不合時宜、表達欠清晰、屬于學習過程中的階段性目標等，這些都會影響學業評價的一致性水平．

第二，可能與命題專家關注度不夠有關，目前“一致性”還沒得到命題專家應有的重視，也未過多考慮試卷的知識種類、廣度和分布情況，進而可能導致試卷的一致性水平不高．

第三，可能與教師一致性素養不高有關．當前教師的一致性理論還不足，開展一致性研究的積極性還不夠，但一致性研究對于提升教學能力又是必要的，它有助于提升教師的專業素養．

第四，研究工具存在自身不足．現階段國內一致性研究都直接采納和編譯國外一致性工具，自編工具較少．值得探討的是，中國與國外教育水平的存在差異，國外理論的適用性還有待進一步考證，因此以國外研究模式按部就班、一字不落地“照搬”在國內研究是不太明智的．為提高試卷與課程標準的吻合程度，可從4個方面改進．

（1）進一步完善課程標準．

課程標準中存在表現型評價缺失和一些不合時宜的具體目標．建議后續課標修訂時，適當加入表現型評價標準，規范學業水平考試，使考試內容、評價體系更為規范、嚴謹．課程標準中的課程內容應與時俱進．只有保證課程標準的科學性和有效性，才能為新一輪“數學核心素養”導向下的人才培養機制相契合，才能為教師的課堂教學和評價保駕護航．

（2）命題基于一致性視角．

試卷命題者在試卷命制的過程中應盡量貼近課程標準，結合一致性研究方法改善命題技術、借鑒命題方法，通過研究相關因素的一致性，借鑒科學的量化比較方法，對存在顯著差異的中考數學試卷進行糾偏和改進，使得中考是基于課程標準的考查，以更好地保證課程標準的全面有效落實．因此，建議命題專家基于一致性視角進行命題．對知識種類而言，需要盡量保持同一領域擊中量不低于6道．對知識深度而言，應準確把握內容標準中的要求．對知識廣度而言，應盡量不重復考查同一目標，對一些較容易忽略的目標可酌情加入，使試卷更具有系統性、綜合性等．

（3）教學實踐融入一致性．

“教師是決定教改成功與否的重要人力資源之一”[18]，一線教師教學應該是基于“課程標準”的實施，而一致性分析是有效檢測教學是否按照標準進行的有力工具，如對期中期末考試試題做一致性檢驗．一方面，可以檢測試題的科學性，進而有效反饋學生應有的水平．另一方面，可以探析課標的實施現狀，也有助于教師更好地理解課標、學業評價和課堂教學3者之間的聯系，進而做到教學實踐立足“雙基”、滲透“數學思想”，幫助學生積累“數學活動經驗”、“領悟”數學核心素養．

（4）研制本土一致性工具．

研制本土一致性工具刻不容緩．目前，開展一致性研究的主流工具并非十全十美，工具在國內的適應性也有待加強．因此，亟需建立一套符合中國國情，完整、系統的研究工具，不僅可以有效檢測學生掌握知識的情況及水平的高低，也可為教育發展、人才培養和選拔發揮重要作用．

[1] 中華人民共和國教育部．基礎教育課程改革綱要（試行）[M]．北京：人民教育出版社，2001：2．

[2] 中華人民共和國教育部．義務教育數學課程標準（2011版）[M]．北京：人民教育出版社，2011：1．

[3] NORMAN L WEBB. Alignment of science and mathematics standards [M]. National Institute for Science Education University of Wisconsin-Madison, 1999: 11-18.

[4] 劉學智．論評價與課程標準一致性的建構：美國的經驗[J]．全球教育展望，2006（9）：35-39．

[5] 劉學智，馬云鵬．美國“SEC”一致性分析范式的診釋與啟示——基礎教育中評價與課程標準一致性的視角[J]．比較教育研究，2007，29（5）：64-67．

[6] 劉學智．小學數學學業評價與課程標準的一致性研究[D]．長春：東北師范大學，2008：1-6．

[7] 崔允漷，王少非，夏雪梅．基于標準的學生學業成就評價[M]．上海：華東師范大學出版社，2008：1-10．

[8] 范立雙，劉學智．美國“成功分析模式”的詮釋與啟示——學業評價與課程標準一致性的視角[J]．比較教育研究，2010，32（8）：77-80．

[9] 張雷．學業評價和課程標準一致性分析模式與個案研究[D]．長春：東北師范大學，2011：1-55．

[10] 楊玉琴，王祖浩，張新宇．美國課程一致性研究的演進與啟示[J]．外國教育研究，2012，39（1）：113-121．

[11] 岳喜騰，張雨強．基于課程標準的學業成就評價：韋伯模式之研究[J]．全球教育展望，2011（10）：79-85．

[12] ?PAUL M, DORIS R, PHOEBE W. State standards and state assessment systems: A guide to alignment council of chief states school officers [M]. Wisconsin: National Institute for Science Education University of Wisconsin-Madison, 1999: 1-43.

[13] 陳嫻，郟璨璨，陳寧．物理內容標準與考試之間的一致性研究[J]．課程·教材·教法，2010，30（7）：67-71．

[14] 周淑紅，王玉文．小學數學核心素養的特質與建構[J]．數學教育學報，2017，26（3）：57-61．

[15] 徐帆，黃莉，張勝元．2017年福建省中考數學卷與課程標準的一致性研究[J]．福建中學數學，2017（7）：1-5．

[16] 胡軍．學生學習成果評價標準不能在課程標準中缺失——澳大利亞科學課程內容與標準給我們的啟示[J]．課程·教材·教法，2005，25（9）：10-14．

[17] 繆琳，陳清華，蘇圣奎．義務教育課程標準與中考試卷一致性分析——以2013—2016年廈門市中考數學試卷為例[J]．數學教育學報，2017，26（5）：44-48．

[18] 駱洪才，昌國良，范凌．義務教育數學課程改革研究階段性評述[J]．數學教育學報，2008，17（3）：23-26．

Study on the Consistency between Mathematics Academic Evaluation and Curriculum Standard in Junior Middle School——Take 5 Sets of Mathematics Examination Papers in Fujian Province as an Example

XU Fan1, ZHANG Sheng-yuan2, SUN Qing-kuo3

(1. No.3 Middle School of Ganzhou, Jiangxi Ganzhou 341000, China;2. College of Mathematics and Informatics, Fujian Normal University, Fujian Fuzhou 350117, China;3. Department of Computer and Mathematics, Nanchang Normal College, Jiangxi Nanchang 330032, China)

The consistency between academic evaluation and curriculum standards couldn’t be ignored. Using Webb analysis model, literature research method, content analysis method and other research methods, the consistency and matching degree between the 5 sets of middle examination papers and curriculum standards were analyzed. The results showed that the matching degree between the 5 sets of examination papers and curriculum standards was not perfect, which may lead to the failure of the feedback function of academic evaluation. Furthermore, in order to improve the conformity between the examination paper and the curriculum standard, suggestions were put forward from the perspectives of curriculum standard revision group, propositions, teachers and researchers. Propositions were based on a consistent perspective, consistency of teaching practice integration, develop local consistency tool.

curriculum standards; academic evaluation; consistency; Webbanalysismodel

2019–01–28

2017年江西省教育科學“十三五”規劃課題——江西城鄉義務教育數學教師有效教學行為對比研究（17YB261）

徐帆（1993—），男，江西南昌人，碩士，主要從事數學課程與教學論研究．

徐帆，張勝元，孫慶括．初中數學學業評價與課程標準的一致性研究——以福建省五套中考數學試卷為例[J]．數學教育學報，2019，28（3）：98-102．

G423.04

A

1004–9894（2019）03–0098–05

[責任編校：陳漢君、張楠]