電動拖拉機永磁同步電機控制系統建模仿真

李宇翔 施愛平 李福強

摘要：永磁同步電機作為電動拖拉機上主要的動力電機有很好的應用前景。針對傳統PID（比例-積分-微分）控制策略對電機轉速控制的響應速度慢、控制精度低的缺點以及Matlab軟件自帶電機模塊的局限性，提出模糊PI自適應控制策略并在電機數學模型的基礎上創建了自定義永磁同步電機（PMSM）模塊，通過Matlab & Simulink仿真軟件，在永磁同步電機矢量控制系統中進行仿真分析。通過對參數的調節得出了理想的輸出曲線，驗證了永磁同步電機模型的合理性、先進性及其控制算法的有效性，為永磁同步電機控制系統設計和電機的調試提供了理論基礎和新的思路。

關鍵詞：永磁同步電機;矢量控制;模糊PI;建模仿真;Matlab & Simulink

中圖分類號： S219.4;TM341? 文獻標志碼： A? 文章編號：1002-1302（2019）10-0224-06

電動拖拉機因其環保、低噪音和操作簡單的特性成為當前農業裝備研究的重點。其中的永磁同步電機的建模和仿真是整機控制的基礎和關鍵。1831年巴洛發明了世界上第1臺永磁同步電機。1983年價格低廉的銣鐵硼永磁材料出現后，永磁同步電機的性能也取得了很大幅度的提高，被廣泛應用于工農業領域中。隨著電力電子技術的進一步發展，永磁同步電機因其體積小、轉矩大、結構簡單、可靠性高等特點成為了電動拖拉機一個可靠的選擇[1-3]。我國稀土資源儲量豐富，尤其是銣鐵硼永磁材料的年產量居世界第一，因此，我們應該大力推動我國稀土產業和永磁同步電機技術的快速發展，以達到減排、保護環境，實現可持續發展，研究永磁同步電機及其控制策略具有重大意義，而建立數學模型并利用計算機仿真技術來研究已成為其研究的主要方法之一。

在矢量控制的眾多方法中最為簡單的研究方法是令 id=0（id為d軸上的電流分量），在Matlab & Sumilink平臺下建立仿真模型并進行仿真，并對仿真結果進行分析。該模型的建立和分析對電機的實際控制及其在電動拖拉機中的應用提供了新的研究思路。

1 永磁同步電機數學模型

以兩相導通星形三相六狀態為例，建立永磁同步電機（PMSM）的數學模型并且分析其電磁轉矩等特性。實際的永磁同步電機的電磁關系非常復雜，為了方便對模型的分析和控制策略的研究，對模型進行簡化分析，并作出如下假設：（1）忽略電機中鐵芯磁路飽和，即忽略電流變化大小對電感參數的影響;（2）不計永磁同步電機磁滯損耗和渦流損耗;（3）定子繞組三相對稱，轉子的磁場在空間呈正弦分布;（4）驅動二極管和續流二極管為理想元器件;（5）轉子上無阻尼套組。

經過坐標變換：將三相靜止坐標a-b-c變換到兩相靜止坐標α-β的變化叫作克拉克（Clark）變換，將兩相靜止坐標α-β變換為兩相旋轉坐標d-q的變化叫做帕克（Park）變換。

2 基于Matlab的永磁同步電機矢量控制模型的建立

在充分分析了永磁同步電機數學模型的前提下，本研究決定采用id=0控制策略，使電機的轉矩控制更加精準從而更好地控制定子電流和轉子速度，構成電流環和速度環的雙閉環結構。永磁同步電機的控制系統結構和系統模型分別見圖1、圖2。

基于矢量控制原理，利用Matlab & Simulink來對永磁同步電機進行建模仿真，根據模塊化思想，可以把永磁同步電機矢量控制分為坐標變換模塊、控制器模塊、空間矢量脈寬調制（SVPWM）模塊、逆變器模塊和PMSM模塊等。通過將這些模塊的有機整合，可以建立PMSM的仿真模型，并且實現對PMSM的有效控制。

2.1 坐標變換模塊

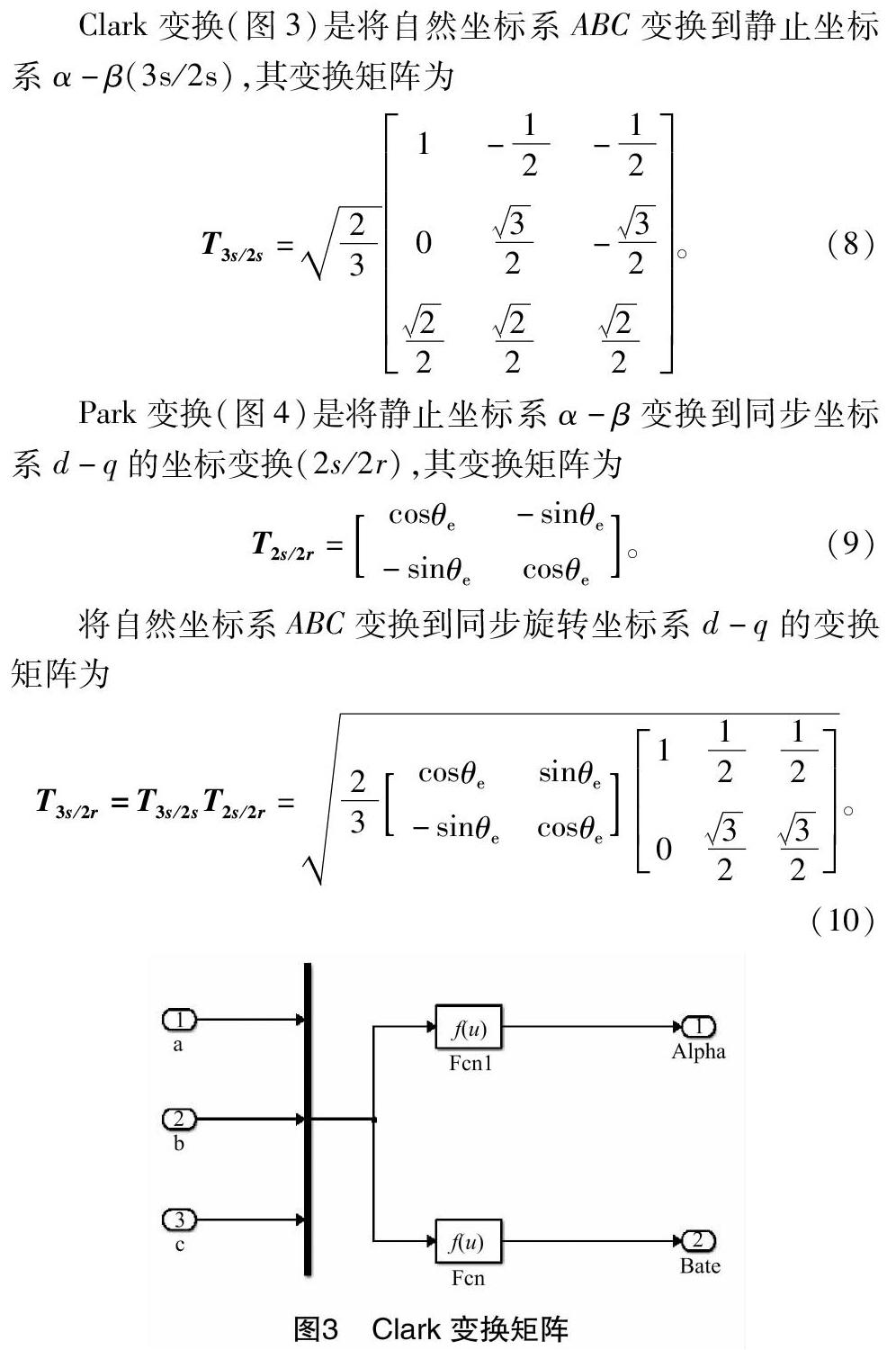
PMSM電機建模的坐標變換用到Clark變換和Park變換。其原理是坐標變換前后變換功率不變，合成磁動勢也不變;作用是將比較復雜的三相靜止坐標參數變換成比較簡單易控制的兩相旋轉坐標參數，簡化了控制方法和過程。交流電機經過Clark變換和Park變換后可以近似看作直流電機。

2.2 速度控制模塊

PID（比例-積分-微分）控制器的傳遞函數為：

速度控制模塊一般采用PI或PID控制方法，但是傳統PID控制策略對電機轉速控制的響應速度慢，控制精度低，以及電機調速系統負載或參數變化時很難達到預期效果。因此，本研究采用的是自適應模糊PI控制方法，因為該控制方法既具有模糊控制靈活、抗干擾能力強、適應性強和魯棒性好的優點，同時兼具高精度控制，而且可以根據偏差和偏差變化率的不同，對參數自動進行在線整定[4]。速度環采用模糊PI設計的主要目的是為了使系統的反饋轉速最大限度地跟隨給定速度，響應速度快，且加強了其抗干擾能力。模糊PI的控制原理見圖5。

自適應模糊PI系統是基于常規PI控制，通過模糊推理思想，將誤差e和誤差變化率ec作為模糊控制器的2個輸入量，并通過其輸出變量，利用模糊規則對PI參數進行實時修正，實現PI參數的最優化。由圖5可知，根據經驗值設定

Kp*和Ki*的值，然后由模糊推理可知修正值ΔKP和ΔKi，最后通過經驗值和修正值得到最優Kp和Ki。其中Kp*和Ki*為經典PI的參數，而ΔKp和ΔKi是模糊PI修正值。設：

速度控制模塊仿真見圖6：

定義e和ec模糊子集為{NB（負大），NM（負中），NS（負小），ZO（零），PS（正小），PM（正中），PB（正大）}，并將模糊子集映射到論域[-3，3]上。將模糊控制器輸出的Kp*和Ki*作為經典控制器的比例、積分，2個參數的修正輸入量重新參與系統的控制，定義其模糊子集為{NB，NM，NS，ZO，PS，PM，PB}，將其論域映射到[-3，3]上。

模糊規則表的建立主要是通過操作者經驗以及對系統運行和性能參數不斷調試的經驗總結[5]。針對輸入量偏差e以及偏差的變化率ec的變化情況，根據表1和表2所示控制規則對ΔKp和ΔKi這2個參數進行在線調整，從而使得控制參數更為精準，同時也讓控制系統擁有更加優秀的動靜態性能[6]。

2.3 SVPWM模塊

當筆者將3相對稱正弦電流輸入到電機中時，電機內部就會產生圓形磁鏈。SVPWM以其為基礎，通過對逆變器開關的不同狀態組合方式，得到8種逆變器開關模式，也就會得到8個基本電壓空間矢量，從而產生有效矢量逼近基準圓[7]。在8種組合電壓空間矢量中，包括6種非零矢量U1（001）、U2（010）、U3（011）、U4（100）、U5（101）、U6（110）和2個零矢量U7（111）、U0（000）。SVPWM技術通過以上6種基本電壓空間矢量中的相鄰有效矢量和零矢量，采用各自不同的作用時間來等效電機所需要的空間電壓矢量。SVPWM算法模擬仿真模型見圖7。

2.4 PMSM模塊

在整個控制系統的仿真模型中，PMSM本體模塊是最重要的部分，反映的是PMSM電機的本質屬性，雖然Matlab & Simulink中的Sim Power System提供了按“Y”形連接的PMSM模塊。如圖8所示，PMSM模塊共有4個輸入端，其中前3個輸入端，分別為A相、B相、C相，第4個輸入端為轉矩輸入的端Tl。

但是隨著技術的發展，仿真應用日益廣泛而且功能要求不斷提高，Matlab & Simulink中的Sim Power System提供的PMSM模塊出現不足，在電機參數在線修改、坐標定義等方面不能滿足仿真要求，給研究帶來不便。例如在對PMSM的定子繞組電阻值做辨識研究時，因為溫度的變化對電阻有一定的影響，所以模擬電阻隨溫度連續變化須要在線修改電阻值[8]。由于Matlab自帶的PMSM模塊不支持在線參數修改，使得類似的變參數仿真的變化量難以考察，從上述例子可知，建立擁有廣泛適用性的電機模型是非常有必要的。因此筆者根據數學模型建立了自定義PMSM模塊，使其在變參數變結構的動態仿真方面更加具有實際意義[9]。根據數學模型建立的PMSM模塊見圖9。

3 仿真分析

因為在永磁同步電機矢量控制中，大功率電機與小功率電機矢量控制模擬仿真系統的三相電流，轉速和轉矩波形曲線大致相同，所以本研究采用功率為2.2 kW的永磁同步電機。根據以上建立的PMSM仿真模型，在Simulink環境下運行電機并且進行該電機矢量控制模擬仿真測試，采用的電機參數如下：電機功率P=2.2 kW;直流電壓Udc=550 V;定子繞組電阻Rs=2.875 Ω;d相繞組ψf=8.5×10-3H;q相繞組 Lq=8.5×10-3H;轉子磁場磁通ψf=0.175 Wb;轉動慣量J=0.8×10-3 kg/m;極對數np=4;B=0。為了驗證該PMSM電機在Simulink環境下工作的動靜態性能，讓電機先空載啟動，當電機進入穩態階段時，在t=0.05 s時突然施加Tl=2 N·m 的負載并且在0.1 s時將電機轉速由300 rad/min增加至3 000 rad/min。系統的三相電流、轉速和轉矩波形曲線如圖10所示。

由圖10-a可知，電機啟動后在4.5 ms內轉速快速上升，并迅速達到穩定狀態轉速300 rad/min，在0.1 s時電機轉速經過0.04 s的加速上升由300 rad/min增至3 000 rad/min并且迅速達到穩定，由此可見電機動態響應性能良好。

由圖10-b可知，PMSM空載轉動時，電機啟動階段大約持續4.5 ms，并且這段時間電機轉矩為 7.6 N·m;0.05 s 時，突然施加負載 Tl=2 N·m，電機經過短暫的波動迅速到達

2 N·m; 0.1 s時轉速突變為 3 000 rad/min 經過0.04 s轉矩由2 N·m上升為7.6 N·m。電機啟動階段和負載運行階段，系統能夠保持轉矩的恒定，沒有產生較大的轉矩，參考電流限幅作用非常明顯，但是由于啟動階段電機轉子的磁場轉速與定子的磁場轉速不同，制動轉矩在短時間內由定子磁鏈和永磁體磁鏈產生的轉矩提供，當牽引轉矩小于制動轉矩時，不考慮電機內部摩擦轉矩，電機總體轉矩會迅速下降為0，從而產生波動;同理當轉速突變為3 000 rad/min時，也會產生類似的波動。

由圖10-c可知，三相點僅在啟動階段電流較大，在 4.5 ms后達到穩定狀態，在0.05 s時施加2 N·m的負載，三相電流會快速響應，在短暫的波動后再次達到新的穩定狀態;在0.1 s轉速突變為3 000 rad/min時電流會再次迅速響應，在0.04 s后達到新的穩定狀態。

由圖10-a可知，電機啟動階段的轉矩（轉速變化量為300 rad/min）與電機轉速突變時間段（轉速變化量為 2 700 rad/min）所需要的轉矩基本相同。如圖11所示，本研究選取不同轉速變化量（選取了300～5 000 rad/min 間的部分數據）并且測定相應的轉矩發現：電機轉速發生變化且轉速變化量小于4 000 rad/min時，轉矩曲線比較平穩，當轉速變化量超過4 000 rad/min時，轉矩將會逐漸減小;當轉速變化量為5 000 rad/min時，轉矩減小為0。當電機轉速變化時，電機轉子的磁場轉速與定子的磁場轉速不同，制動轉矩短時間內由定子磁鏈和永磁體磁鏈產生的轉矩提供，可以使轉子磁場速度與定子磁場速度相同，當轉速變化量超過 5 000 rad/min 時，電機無法提供對應的轉矩，所以會造成電機丟步，如果持續時間較長，會對電機造成不可逆的損壞。

4 結論

本研究在基于Matlab & Simulink的基礎上，搭建了整個永磁同步電機控制系統速度和電流雙閉環仿真模型，電流控制和速度的控制分別由電流滯環控制和模糊PI自適應控制方法來實現。仿真結果表明，波形符合理論分析，系統的平穩性比較好，響應快，并且具有良好的動態效果和靜態效果，符合永磁同步電機的運行特性，并且本研究討論了轉速變化量與轉矩的關系，為矢量控制的實現提供了基礎并為永磁同步電機的設計和調試提供了新思路。

參考文獻：

[1]李崇堅. 交流同步電機調速系統[M]. 北京：科學出版社，2006.

[2]de Almeida A T，Ferreira F J T E，Fong J A C . Standards for efficiency of electric motors[J]. IEEE Industry Applications Magazine，2011，17（1）：12-19.

[3]Wooldridge M，Jennings N R. Intelligent agents：theory and practice[J]. The Knowledge Engineering Review，1995，10（2）：115-152.

[4]卞延慶，莊 海，張穎杰. 基于模糊PI的永磁同步電機矢量控制研究[J]. 微電機，2015，48（11）：62-67.

[5]秦燦華，劉連根，曹 洋，等. MW級永磁同步電機無速度傳感器矢量控制研究[J]. 湖南工業大學學報，2012，26（1）：37-40.

[6]楊 勇. 基于模糊自整定的改進型永磁同步電機矢量控制仿真研究[J]. 機電工程技術，2010，39（8）：47-49.

[7]白繼榮，李橋梁，黎志光. 帶轉矩和磁鏈內環的交流異步電機矢量控制系統仿真[J]. 電機技術，2008，29（2）：1-4.

[8]Wilson S D，Stewart P，Taylor B P. Methods of resistance estimation in permanent magnet synchronous motors for real-time thermal management[J]. IEEE Transactions on Energy Conversion，2010，25（3）：698-707.

[9]王莉娜，楊宗軍. Simulink中PMSM模型的改進及在參數辨識中的應用[J]. 電機與控制學報，2012，16（7）：77-82.