深究，讓探究指向數學核心素養培育

摘? 要：“探索規律”是小學數學教材中不同于基礎知識的一條內容線索，第二學段更是獨立編排，不屬于《義務教育數學課程標準》規定的必學和必考內容。其有趣的專題、問題解決式的編排、超越雙基的彈性化要求，對于培養高層次數學核心素養具有獨特價值。數學核心素養引領下的規律探索，不僅要探究，更要深究。讓探究與精準分析、多維探析、深層剖析等有機整合，推動數學核心素養由問題解決走向數學思維把握乃至理性精神培育。

關鍵詞：數學核心素養;深究

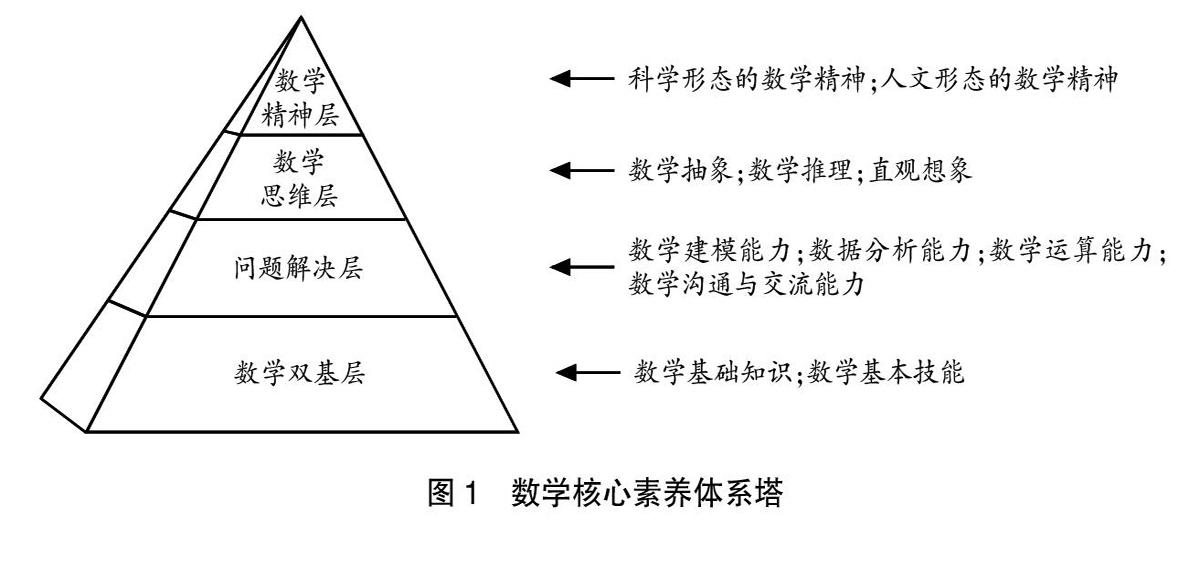
研究表明，數學核心素養體系可以劃分為由低到高的四個層面：數學雙基層、問題解決層、數學思維層、數學精神層。如圖1。

“探索規律”是小學數學教材中不同于基礎知識的一條內容線索，第二學段更是獨立編排，不屬于《義務教育數學課程標準》規定的必學和必考內容。其有趣的專題、問題解決式的編排、超越雙基的彈性化要求，對于培養高層次數學核心素養具有獨特價值。數學核心素養觀照下的規律探索，不僅要探究，更要深究;不僅要動手，更要動腦;邊探邊思，探思結合，讓規律探索不斷指向高層次數學核心素養的培育。下面僅以蘇教版四年級“多邊形內角和”為例，談談具體的做法。

一、精準分析，涵養抽象眼光

情境1：探索四邊形的內角和。

教師一般讓學生依據三角形內角和以及從特殊到一般的思路，自主提出四邊形內角和問題并展開探究。學生發現，四邊形中最特殊的是長方形、正方形，它們的內角和都是360°，從而容易提出所有四邊形的內角和可能都等于360°，進而從相對特殊的平行四邊形和直角梯形等入手進行繼續探究。然而交流展示時不難發現，學生想到的幾乎都是“量”與“拼”，很少有學生能自主想到“分”。

“量”和“拼”本質上都是“做”，而“分”本質上是“看”，這種“看”實際是利用四邊形與三角形之間的關系，由三角形內角和推理得到四邊形的內角和。從“量”和“拼”拓展到“分”，并非只是方法數量的增加，更是涉及了方法視角的改變，即由感性的直觀操作過渡到相對抽象的邏輯推理。學生之所以不能自主想到“分”，是因為學生無法自主建立起這樣一種“抽象”的眼光。

研究表明，這種抽象一般要經歷兩個層次：對應和內涵。所謂對應，就是給這種方法起個名字;所謂內涵，就是要分析它的本質。在上述教學中要讓學生戴上“分”這樣一副抽象的“眼鏡”，需要教師適時點撥：這些圖形與已經學過的三角形有什么關系？你能用三角形的內角和推算出它們的內角和嗎？更需要精準分析：這種“分”與過去所學的“量”和“拼”有什么不同？教學實踐表明，適時點撥能讓大多數學生能輕松想到用“分”的方法去求平行四邊形和梯形的內角和，并以此為基礎推算一般四邊形的內角和;適時分析，能讓大多數學生理解這里的“分”本質上是由動手實驗轉換到動腦推理，借助推理探求新知。一系列深究，使得抽象的眼光得以真正建立。

二、多維探析，引發高階思維

情境2：探索五邊形、六邊形的內角和。

教師提供五邊形、六邊形材料，同桌兩人運用“分”的方法，由三角形的內角和探究五邊形、六邊形的內角和。交流展示時可以發現，五邊形相對容易，有的學生甚至還想到了把五邊形分成一個四邊形和一個三角形，但評講時教師對該分法視而不見;六邊形相對困難，不少學生無從下手。通過課后訪談筆者了解到，教師之所以對學生的“另類”分法持忽略態度，是源于其認為該分法所對應的算法與最后的一般算法不一致，它的呈現會干擾規律的探索與發現。

從四邊形到五邊形、六邊形，隨著邊數增加，研究的對象變得越來越復雜，方法也變得越來越多元，對思維的要求也越來越高。澳大利亞學者比格斯曾提出SOLO思維結構分類理論，該理論認為，不論是兒童還是成人，高層次思維結構的形成一般要經歷前結構、單一結構、多元結構、關聯結構、抽象拓展結構等五個階段。由此看來，學習四邊形內角和時剛剛掌握的“分”法，只是將“前結構”提升為一種清晰的新結構，該結構還非常膚淺、簡單，屬于“單一結構”階段，所以五邊形的遷移相對容易，而六邊形探究相對困難。

顯然，在后續學習中，多元方向的探究有可能實現思維的突破。因而上述五邊形的“另類”分法，其實是一種可貴的探索。雖然它可能意味著該學生尚未認識到分割最佳的結果（三角形），表征著一種低層次的轉化，但它卻呈現了難得的另一種可能。因此，教師應及時肯定該學生的想法和算法，進而展開深究：仔細觀察其中的四邊形，聯系剛剛所學的四邊形分法，你又有什么發現？引導學生感悟遞推的美妙，理解分成三角形的奧妙，嘗試將這些分法運用到六邊形的探究中。

教學實踐表明，單一結構一旦被突破，學生還能找到更多“分”法，如從一個頂點開始，由內部的一個點出發，抑或從某條邊上的某一個點出發，等等。不過，高階思維的建構還需要進一步深究：這些貌似不同的“分”法有沒有相同的地方呢？不少學生能認識到，“分”法雖有所不同，但最終都可以分成若干個三角形，都恒等于若干個180°。這樣，深究又讓高層次的關聯結構、抽象結構的把握成為現實。

三、深層剖析，激活直觀想象

情境3：探索多邊形內角和的一般規律。

教師讓學生自己畫出一些七邊形或八邊形，繼續用“分”的方法探索它們的內角和，再按照圖形名稱、邊數、分成的三角形個數、內角和等，把已有探究結果整理成表格，看看有什么發現。在教學現場可以看到，對學生來說，畫出七邊形、八邊形等更為復雜的多邊形似乎是一個不小的挑戰，列表整理也多是一種耳提面命式的操作。

多邊形有凸多邊形和凹多邊形，小學階段沒有特別說明，就默認為凸多邊形范疇。筆者曾嘗試畫出七邊形、八邊形等，發現一不小心就畫成了凹著的七邊形和八邊形，這里讓學生畫多邊形，可能會讓他們遭遇到凹多邊形的情形，從而超越最近發展區。

不過，這種探究并非沒有價值，關鍵要使之成為提升思維水平的一個契機，而這一目標的達成還是離不開深究。不妨在學生動手探究遇到困難時，適時提問：隨著邊數的增加，多邊形變得越來越復雜，“分”還是一種很好的方法嗎？從而讓學生感受到“分”法的局限性;進而追問：動手操作已經不能很好地解決問題了，能不能動動腦筋找找其中是否蘊藏著什么規律呢？從而讓列表整理成為模型思想引領下的探究，而非盲目的數學運作。

相關規律的解釋，如多邊形內角和為什么總與三角形內角和有關？分成的三角形的個數為什么總比多邊形的邊數少2？可以引導學生由簡單圖形激活對復雜多邊形的直觀想象，借助想象剖析：因為多邊形都可以分成若干個三角形，而分成的三角形中，總有兩個三角形中的兩條邊是多邊形的邊，而其余的三角形，都只有一條邊是多邊形的邊，所以三角形的個數總比多邊形的邊數少2，從而實現對算法模型及其要素關系的通透理解。

對照數學核心素養體系塔的更高目標，不難發現，多邊形內角和的探究，還需要更為深入的反思：其方法從“量”與“拼”到“分”，再從“分”優化為“算”，這些變化是否僅僅出于簡便的考慮？對于某一個多邊形來說，如果“量”的結果與“算”的結果不一致，是不是一定意味著“算”錯了？讓學生感悟這個規律并非動手測量的直接結果，而是人類理性思維綻放的花朵，進而讓學生數學核心素養的培育由數學思維的把握走向更高層次的數學精神的領悟。

總之，數學核心素養引領下“探索規律”的教學，需要教師把一系列連貫的規律探究活動合理地劃分為若干個環節，讓探究適時與深究整合，引導學生由問題解決層走向數學思維層，訓練抽象、推理、想象等數學思維方式;讓深究適時與反思結合，引導學生由數學思維層進一步走向數學精神層，洞悉數學獨特的理性和人文精神。

基金項目：此文系江蘇省教育科學“十二五”規劃（2015年度）課題“小學數學教學領域操作要義的創新研究”（編號：D/2015/02/285）成果之一。

作者簡介：朱潔芬（1966-），本科學歷，教育碩士學位，中小學高級教師，從事小學數學教學。