核心素養背景下的小學數學高效課堂

摘? 要：為了讓課堂更高效，這就需要我們去捕捉學生的困惑，以此開展深度教學，讓每個學生的思維更有廣度和深度，使得“數學思考”這一課程目標得到真正的落實。

關鍵詞：思維的困惑;弄清算理;澄清差異;將錯就錯

在課堂教學中我們經常遇到一小部分學生思維跑偏的現象，老師只是用“對”或“錯”來淺層解讀，不去弄清思維跑偏的原因，認為小部分學生思維跑偏無關緊要。其實不然，這一小部分學生思維出現的錯誤恰恰正是相當一部分學生思維的困惑之處，只是這部分學生在形式上隨了大流，沒有暴露出來，這是暫時的。因為學生的思維過程是復雜的，不同的學生在面對同一個數學問題，思路有相同和相似的地方，但也會有不同之處。只有讀懂了學生的思維，用不同的方法去開展深度教學，才能讓每個學生的思維更有廣度和深度，讓課堂教學變得更高效。

一、弄清算理，補上斷層

學生在計算時常常出錯，這是因為學生學習計算需要有一個理解算理再到歸納算法的知識升華過程，這就要經歷具體算法的充分體驗過程才能形成熟練的計算技能。在運用算法的過程中，學生往往會出現這樣或那樣的錯誤。出現的錯誤有些是計算能力差，比如乘法口訣出錯或者加減乘除四則運算的順序出錯，更有甚者是基本口算不過關，另外還有一些是“非主流”性的錯誤，主要是對每一步的具體算理沒有真正理解，對于計算方法的應用只是一種簡單機械的模仿，對細節的區分不到位，而導致出錯。

例如，教學三年級兩三位數除以一位數，有關“商中間或者末尾有零的除法”時，筆者出示例題是這樣的：

在練習中，少數學生在計算600÷4時出現了以下的錯例。

師：為什么你的商中在末尾是兩個0呢？

生：0除以任何不是0的數都得0，而600這個數的十位和個位上都是0，所以商的末尾就有兩個0。

師：那么你的余數是多少？

生：200。

另外的同學說道：不對的，這樣余數就比除數大了。

師：這樣一改對嗎？

有的學生又陷入了困惑之中。

師：為什么會出現這樣的問題呢？讓我們一起討論一下吧！

……

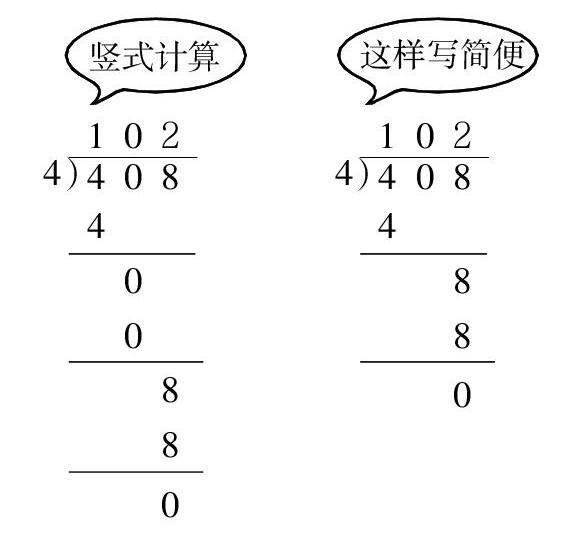
在例題中出現了這樣的一個負遷移點：被除數的哪一位上有0，那一位的商就寫0。這個問題反映出了一部分學生的思維真相——沒有弄清算理，只是一個簡單的模仿。在學習例題時，408÷4=102，商中間的0產生在百位上，正好是在余0的前提下，十位上0除以4商中間也就為0了，從而有的學生誤認為只要被除數中間遇到0，就不用除了，直接在那一位上商0就可以了。這樣本質的東西學生沒有學會，只是流于形式，遇到被除數哪一位上有0，就直接在那一位上商0。經驗的負遷移對于一部分還未真正理解算理的學生來說是經常出現的，有些學生在學了一段時間后還會出現這樣的問題。此時，老師應該讀懂學生，讓這種負遷移就地消除，防患于未然。

接下來，老師帶領學生先弄清算理，在計算三位數除以一位數時，先從最高位算起，在600÷4時，盡管被除數的十位上是0，但百位上6除以4后還余2，表示2個百，和十位上的0合成20個十，因此十位上應該是20個十平均分成4份，所以商5，這時十位上正好分完，然后個位上是0÷4就得0，因此商的末尾只有一個0。就這樣通過算理補上了學生思維的斷層，從而真正避免學生在以后計算中只是對于算法形式上的模仿，達到“通其法，明其理，防出錯”之效。

二、比對題組，澄清差異

在學生學習過程中，我們經常遇到一類問題，它們外貌特別相似，實質卻相差千里，但由于外形的相近性，蒙蔽了不知多少學生，讓他們身陷“囹圄”，叫苦不迭。面對現狀，在教學上，我們可以精心設計題組，故布疑陣，通過題組的鮮明比對，突出差異，引導學生悉心對比、辨析，幫助學生澄清差異，從而消除一些模糊認識，防止知識的泛化、混淆，彰顯內在本質屬性，縝密學生的思維，培養學生一絲不茍、孜孜以求的學習品質。正如著名教育家烏申斯基所言：比較是一切理解和思維的基礎，我們正通過對比來了解世界上的一切。故此，在新知教學中，筆者在精心設計對比題性題組上下功夫，大大優化了學生數學思維的深度和廣度，作用不凡，收到了優質的教學成效。

例如，計算：

以上這兩個豎式中的數據是完全相同，所不同的是運算符號。

師：以上計算的過程中有哪些是相同的，哪里是不同的？

生：計算的方法是相同的，都要把小數點對齊，也就是數位對齊，都是從低位加起和減起。不同的是在算百分位上的數時，加法中的一個加數6.2的百分位上沒有，可以將另一個加數2.86的百分位上的數6落下來，但是減法不行。

師：為什么減法中不可以直接將6落下來呢？

生：因為加法中6.2的百分位上沒有，根據小數的基本性質可以在2后面添0，0+6得6，所以2.86的百分位上的數6直接落下來就可以了，但是減法中0-6不得0，而是不夠減要向十分位借……

通過讓學生對兩個相似高度很高的對象的比較，可以使學生對于小數加減法的算理和算法理解得更加牢固和深刻。

再如計算：

以上這兩個豎式中的數據是完全相同，所不同的也是運算符號。

生：

師：以上兩道題都正確嗎？有沒有另外的方法來檢驗一下呢？

生：可以先算出括號里面，再計算。

師：咦！第二道的計算結果怎么不一樣呢？

生：大家陷入沉思之中。

師：乘法有分配律，而除法有分配律嗎？

生：如夢方醒，對呀！除法沒學過分配律。

數學符號的世界，是數學簡約性、抽象性的體現，符號是數學交流的一類語言，由于其單薄，所以它比字詞更容易被漠視，通過比對題組，澄清差異。看似細小的差異，它們會興風作浪，我們要有孫悟空的火眼金睛，透視外表，洞察其里，直擊內核，什么“妖魔鬼怪”都會不在話下。

三、將錯就錯，柳暗花明

學生出現的錯誤不可能單獨依靠“堵”來實現，正如大禹治水巧妙采用了“疏”的方式，成功治水。學生對錯誤的認識也是這樣，它是一個“自我否定”的過程，而“自我否定”以自我反省，特別是內在的“觀念沖突”作為必要的前提。利用學習中出現的錯誤，并及時引發這種“觀念沖突”，能促進學生對已完成的思考過程進行周密且有批判性的再思考，對已形成的認識從另一個角度，以另一種方式進行再思考，以求得深入認識，這既有利于問題的解決，又能培養學生的思考能力。

例如，在教學“平行四邊形的面積”一課時，有的同學大膽提出“平行四邊形的面積就是相鄰的兩條邊的相乘”。

師：你能說說你的猜想依據嗎？

生：長方形、正方形都是特殊的平行四邊形，長方形和正方形的面積是長乘寬，是相鄰的兩條邊相乘，所以平行四邊形的面積也可以是用相鄰的兩條邊相乘。

師：說得有道理，到底是不是這樣呢？還需我們大家動手去驗證。

生：我發現捏住平行四邊形的一組對角向兩邊拉，平行四邊形兩條邊的長度沒變，可面積變小了，所以不能用相鄰的兩條邊相乘來計算平行四邊形的面積，我還發現平行四邊形的面積變了，高也變了，所以面積一定和高有關系。

生：我通過畫圖、剪拼、測量計算，推導出了平行四邊形的面積是底乘高。

這樣通過學生的探索、討論，不僅學生糾正了錯誤，還發現了平行四邊形面積的計算方法，理解公式的由來，進一步認識了平行四邊形和長方形、正方形面積計算公式的聯系與區別，正是錯誤的結論，激發了學生探究的興趣，也就是教師以學生課堂生成的錯誤為契機，巧妙運用差錯資源而產生的效果。想必在這樣的課堂教學中學生的批判精神、科學意識和用數學思考的能力在無形中都得到了加強。

正確，可能只是一種模仿;而錯誤，卻絕對是一種經歷。教師需要始終站在關注學生發展需求的角度來審視自己的教學行為，去追尋學生思維發展的有效途徑，去挖掘隱藏在教材中的數學思考。利用錯誤“將錯就錯”，體會數學思考的“柳暗花明”！只有這樣，我們的數學課才能更有“數學味”！也只有這樣，“數學思考”這一課程目標才能得到真正的落實。

基金項目：山東省教育科學“十二五”規劃教學專項課題“利用信息技術提升學生數學核心素養的實施策略研究”（課題批準號：XJ0194）;數字化學習規劃課題“直接獲取式微課資源研究”（課題批準號：2017BB125）。

作者簡介：李俊峰（1977-），本科學歷，中小學一級教師，從事小學數學教學及研究工作，2015年3月在濱州市首屆中小學微課程評選活動中獲一等獎;2015年參與了青島版小學數學教學參考用書的編寫。