關聯圓錐曲線焦點、準線的一個性質的推廣
陳建海


1 問題的提出
《福建中學數學》2018年第6期文[l]對一道課本例題進行逆向探究,得到了關聯圓錐曲線焦點、準線的的一個性質,即下面的性質1-4(即文[l]的“一般性的結論”).讀后頗受啟發,但覺意猶未盡,本文擬對上述性質進行推廣.先把文[l]的性質1-3及“一
般性的結論”抄錄如下:
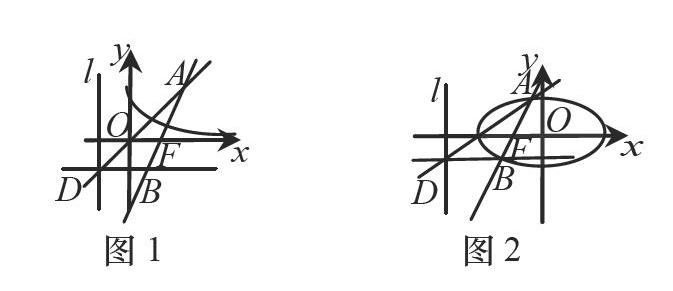
性質1過拋物線焦點F的直線交拋物線于A,B兩點,點D在拋物線的準線上,若直線BD平行于拋物線的對稱軸,則直線AD經過拋物線的頂點O(如圖1).
性質2過橢圓焦點F的直線交橢圓于A,B兩點,點D在焦點F對應的準線上,若直線BD平行于橢圓的對稱軸,則直線AD經過定點(該定點是準線與對稱軸的交點和焦點F的連線段的中點)(如圖2).
性質3過雙曲線焦點F的直線交雙曲線于A,B兩點,點D在焦點F對應的準線上,若直線BD平行于雙曲線的對稱軸,則直線AD經過定點(該定點是準線與對稱軸的交點和焦點F的連線段的中點).
性質4(即文[1]的“一般性的結論”)過圓錐曲線焦點F的直線交圓錐曲線于A,B兩點,點D在焦點F對應的準線上,若直線BD平行于圓錐曲線的對稱軸,則直線AD經過定點(該定點是準線與對稱軸的交點和焦點F的連線段的中點).
以上性質揭示了關聯圓錐曲線焦點、準線的一個性質,那么,這個性質對圓錐曲線的“類焦點”、“類準線”能否成立?即能否把上述性質推廣到“類焦點”、“類準線”的情形?
2 性質的推廣
經探究發現,以上性質不僅對圓錐曲線的焦點、準線適用,而且對圓錐曲線的“類焦點”、“類準線“也適用.可以把上述性質推廣到“類焦點”、“類準線”的情形.
性質1-1過拋物線“類焦點”F的直線交拋物線于A,B兩點,點D在拋物線的“類準線”上,若直線BD平行于拋物線的對稱軸,則直線AD經過拋物線的頂點O.
證明 如圖l,以拋物線的頂點O為原點,拋物線的對稱軸為x軸,建立直角坐標系.設拋物線的方程為y2=2px(p>o),“類焦點”F(m,o)(m>o),“類準線”x=一m與x軸的交點坐標為(一m,o).下面分兩種情況證明.
當直線AB的斜率存在時,
設直線AB的方程為y=k(x一m)(k≠o).
得k2(X-m)2=2px,
整理得k2X2—2(k2m+p)x+k2m2=0.
設A(x1,Y1),B(X2,y2)(Xl≠X2),
據韋達定理得:
則直線AD經過定點(o,o),
即拋物線的頂點O. 當直線AB的斜率不存在時,
則直線AD經過定點(o,o),
即拋物線的頂點O.
性質2-1過橢圓“類焦點”F的直線交橢圓于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線BD平行于橢圓的對稱軸,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點).
證明如圖2,以橢圓的中心O為原點,橢圓實
軸所在的直線為x軸,建立直角坐標系.
下面分兩種情況證明.
當直線AB的斜率存在時,設直線AB的方程為y= k(x-m)(k≠0).(注:若K=o,則結論顯然成立).得b2X2+ a2k2 (X- m)2 _a2b2=o,∴(a2k2+b2)X2—2a2k2mx+a2k2m2一a2b2=0.設A(x,Yi),B(X2,y2 )(Xl≠X2),據韋達定理得X1十X2:2a2k2m
該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點.
當直線AB的斜率不存在時,
該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點.
類似地,可以把性質3推廣為:
性質3-1過雙曲線“類焦點”F的直線交雙曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線BD平行于雙曲線的對稱軸,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點). 一c時,性質2-1、3-1分別為性質2、3.
由性質I-I、2-1、3-1,可把性質4推廣為:
性質4-1過圓錐曲線“類焦點”F的直線交圓錐曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線BD平行于圓錐曲線的對稱軸,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點).
3 推廣性質的逆命題
上述推廣性質的逆命題成立嗎?只要對性質4-1進行討論即可.設過圓錐曲線“類焦點”F的直線交圓錐曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線AD經過“類準線”與對稱軸的交點和“類焦點”F的連線段的中點M,那么直線BD是否平行于圓錐曲線的對稱軸?
設點D1在類焦點“F對應的“類準線”上,且直線BD,平行于圓錐曲線的對稱軸,據性質4-1,得直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點M).這表明直線AM經過點D1.又直線AD經過“類準線”與對稱軸的交點和“類焦點”F連線段的中點M,知直線AM經過點D,則點D,D1同為直線AM與“類準線”的交點,故點D,D1重合,從而直線B平行于圓錐曲線的對稱軸,
可見,性質4-1的逆命題成立,其逆命題是:
性質4-2過圓錐曲線“類焦點”F的直線交圓錐曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的的中點),則直線BD平行于圓錐曲線的對稱軸,
據此,可得性質I-I、2-1、3-1的逆命題:
性質1-2過拋物線“類焦點”F的直線交拋物線于A,B兩點,點D在拋物線的“類準線”上,若直線AD經過拋物線的頂點O,則直線BD平行于拋物線的對稱軸.
性質2-2過橢圓“類焦點”F的直線交橢圓于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點).則直線BD平行于橢圓的對稱軸.
性質3-2過雙曲線“類焦點”F的直線交雙曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,若直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點),則直線BD平行于雙曲線的對稱軸.
特別地,當“類焦點”F為焦點時,性質1-2、2-2、3-2、4-2分別為性質1、2、3、4的逆命題.
4 所得結論的完善
分別綜合性質l-I、1-2,2-1、2-2,3-1、3-2,4一、4-2,可得:
性質1-3過拋物線“類焦點”F的直線交拋物線于A,B兩點,點D在拋物線的“類準線”上,則直線AD經過拋物線的頂點O的充要條件是直線BD平行于拋物線的對稱軸.
性質2-3過橢圓“類焦點”F的直線交橢圓于A,B兩點,點D在“類焦點”F對應的“類準線”上,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點)的充要條件是直線BD平行于橢圓的對稱軸.
性質3-3過雙曲線“類焦點”F的直線交雙曲線于A,B兩點,點D在“類焦點”F對應的“類準線”上,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點)的充要條件是直線BD平行于雙曲線的對稱軸.
性質4-3過圓錐曲線“類焦點”F的直線交圓錐曲線于AB兩點,點D在“類焦點”F對應的“類準線”上,則直線AD經過定點(該定點是“類準線”與對稱軸的交點和“類焦點”F的連線段的中點)的充要條件是直線BD平行于圓錐曲線的對稱軸.
參考文獻
[1]孫承雄,對一道課本例題的逆向探究[J].福建中學數學,2018 (6):7—8

