適用于輪轂電機驅動電動汽車的ABS控制邏輯研究＊

李敏 楊坤 王杰 田昭賢 李鵬程

（山東理工大學，淄博 255000）

主題詞：輪轂電機 制動防抱死系統 車輪轉動慣量 邏輯門限值控制 正交試驗

1 前言

輪轂電機驅動電動汽車因具有高集成化、高效率和獨立可控的優勢而成為未來高性能電動汽車的發展方向之一，適用于輪轂電機驅動電動汽車的制動防抱死系統也開始受到關注[1-7]。

近年來，國內外對輪轂電機驅動電動汽車開展了大量研究，其制動安全性逐步引起人們的重視[8-9]，但制動方面的研究主要集中于制動能量回收，制動系統均采用了與傳統車相同的ABS。通過前期研究發現，由于輪轂電機的應用使得車輪轉動慣量大幅增加[10]，這對于傳統ABS在輪轂電機（IWM）驅動電動汽車中的控制效果有較大影響，主要體現為：車輪對制動力矩的響應遲鈍，需要更大的制動力矩才能獲得較大的制動減速度；車輪角速度變化率低，車輪減速度達不到門限值就會進入不穩定狀態，可能導致車輪過早抱死，使ABS控制邏輯失效，進而影響車輛的行駛安全[11-13]。因此，研究車輪轉動慣量大幅增加對ABS控制邏輯的影響規律并開發適用于輪轂電機驅動電動汽車的ABS控制邏輯具有重要意義。本文對此開展了理論研究，利用正交試驗法對ABS控制邏輯的合理性進行分析，基于MATLAB/Simulink搭建了7自由度模型，對車輪轉動慣量增加所引起的車輛制動性能變化進行分析，以期為輪轂電機驅動電動汽車ABS控制策略中控制門限值的合理確定提供理論依據。

2 ABS控制算法

2.1 轉動慣量增加對ABS的影響分析

輪轂電機驅動電動汽車將電機、減速機構等集成在車輪內部，導致車輪轉動慣量顯著增加，從而顯著影響車輪運動特性：

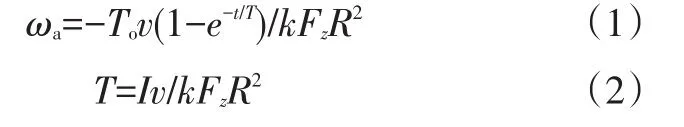
式中，ωa為車輪制動角加速度；To為制動器制動因數；v為車速；t為時間；T為制動減速度動態特性決定因子；k為輪胎特性曲線斜率；Fz為車輪對地面的法向反力；R為車輪半徑；I為車輪轉動慣量。

式（1）表達了附著系數最大時刻的車輪角加速度，式中常數Tov/kFzR2決定了到達最佳滑移率時車輪所能達到的最大制動減速度。由式（2）可以看出，大的轉動慣量將使T變大，而T決定了在最佳滑移率處達到最大制動減速度快慢的動態特性，該動態特性對確定最佳門限值有重要意義，即轉動慣量增加會影響ABS門限值的選擇，從而影響ABS的控制效果。

2.2 ABS控制流程

過去，人們雖針對ABS控制算法開展了大量研究，但是產品化的ABS仍采用邏輯門限值控制算法[14-16]。本文以車輪角加、減速度門限值和參考滑移率作為控制量，以使汽車具有較短的制動距離和更好的制動穩定性為目標，提出了相應的控制策略，以高附著系數路面為例的ABS控制流程如圖1所示，圖1中，-a、s、s1、+a、+Ak分別為角減速度門限值、滑移率、滑移率門限值、角加速度門限值、角加速度上限值。

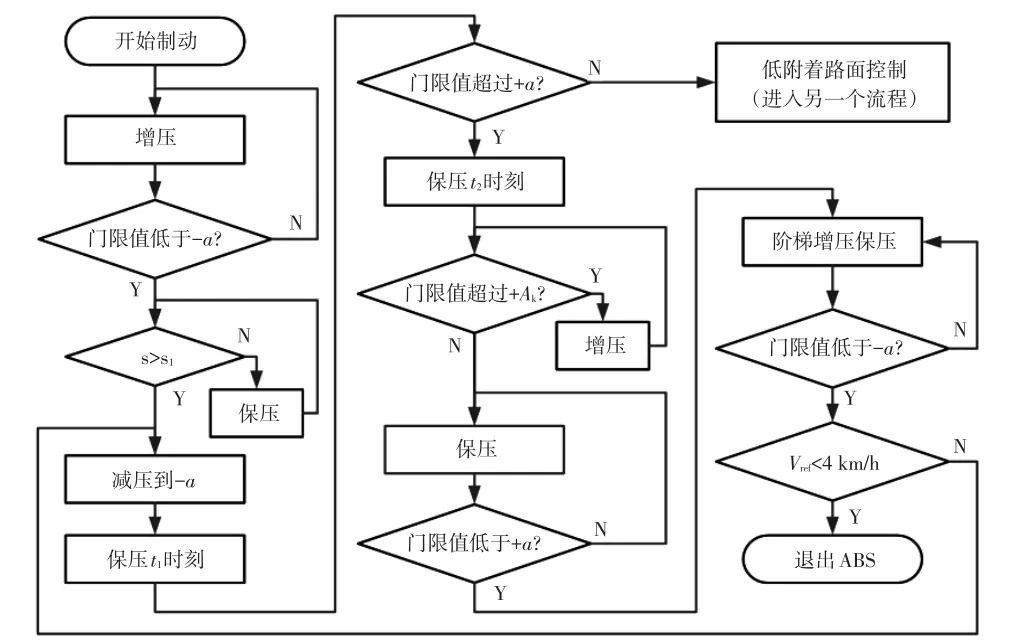
圖1 高附著路面ABS控制流程

2.3 ABS的邏輯門限值控制模型

基于圖1所示的控制流程，在MATLAB/Stateflow下搭建了如圖2所示的ABS控制模型。ABS控制邏輯包括ABS開啟、關閉、退出，以及增壓、減壓、保壓和階梯增壓7個狀態。各狀態之間根據車輪的角減速度或者滑移率進行切換，切換條件如表1所示，各狀態下制動力矩的調節斜率d的取值如表2所示。表2中，不同狀態下斜率的取值d0、d1、d2、d3依次遞減，其值通過標定確定。

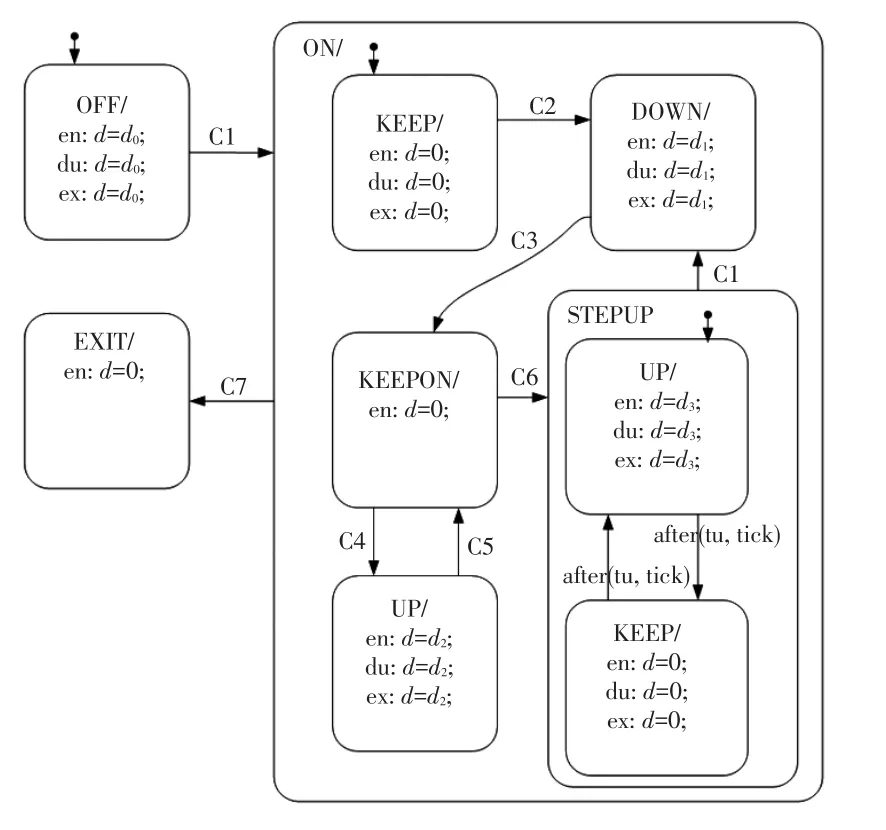
圖2 ABS控制模型

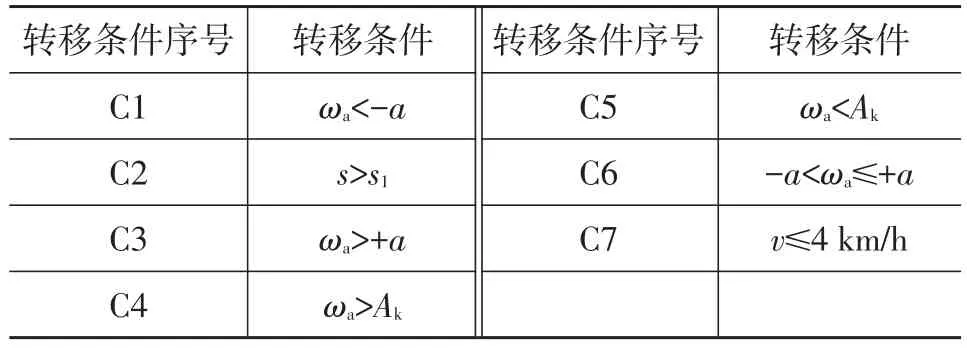
表1 控制邏輯狀態切換條件

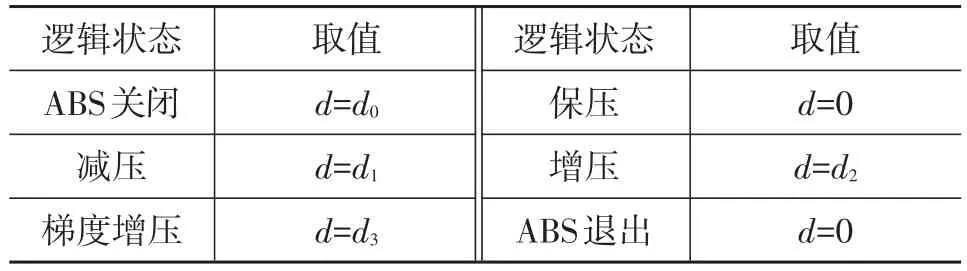
表2 控制邏輯狀態取值

2.4 最佳門限值確定方法

正交試驗是利用正交表來設計多因素、多水平試驗，并采用統計學方法分析試驗結果的一種試驗設計方法[17-18]。它利用正交表來安排少數次試驗，通過對這部分試驗結果進行分析計算，確定各因素的主次順序，選取最優的水平組合。本文以制動距離和制動時間作為考察指標，設計了角減速度門限值A、滑移率門限值B、角加速度門限值C三因素三水平的正交試驗和L9(33)正交表。

角減速度門限值應大于高附著路面峰值附著系數對應的車輪角減速度，同時小于低附著路面峰值附著系數對應的車輪角減速度，為此，取中等附著系數路面滑移率為7%～15%時的車輪角減速度。滑移率門限值取值過小時，制動過程中車輪對地面附著條件利用不足，滑移率門限值取值過大時，制動過程中車輪可能抱死，為此，滑移率門限值的取值范圍設置為7%～15%。角加速度門限值取值過小時，會導致輪速還未充分恢復即進入增壓階段，從而使增、減壓狀態頻繁切換，制動強度不足；角加速度門限值取值過大時，輪速會因無法達到門限值而使車輪一直處于恢復狀態，導致過度減壓，制動力不足，制動距離加長。因此，本文中角加速度門限值的水平取值范圍為0～19 rad/s2，具體取值如表3、表4所示。

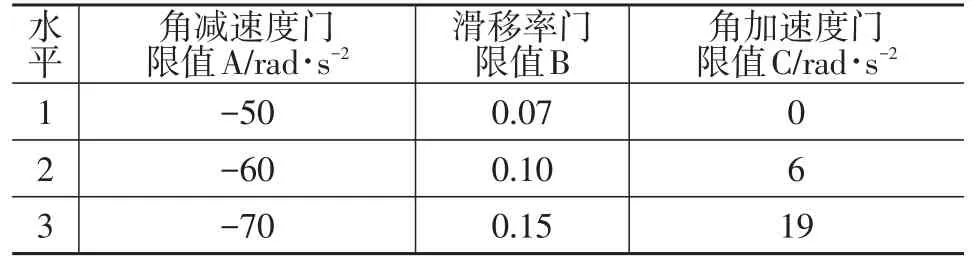
表3 試驗的因素及水平取值

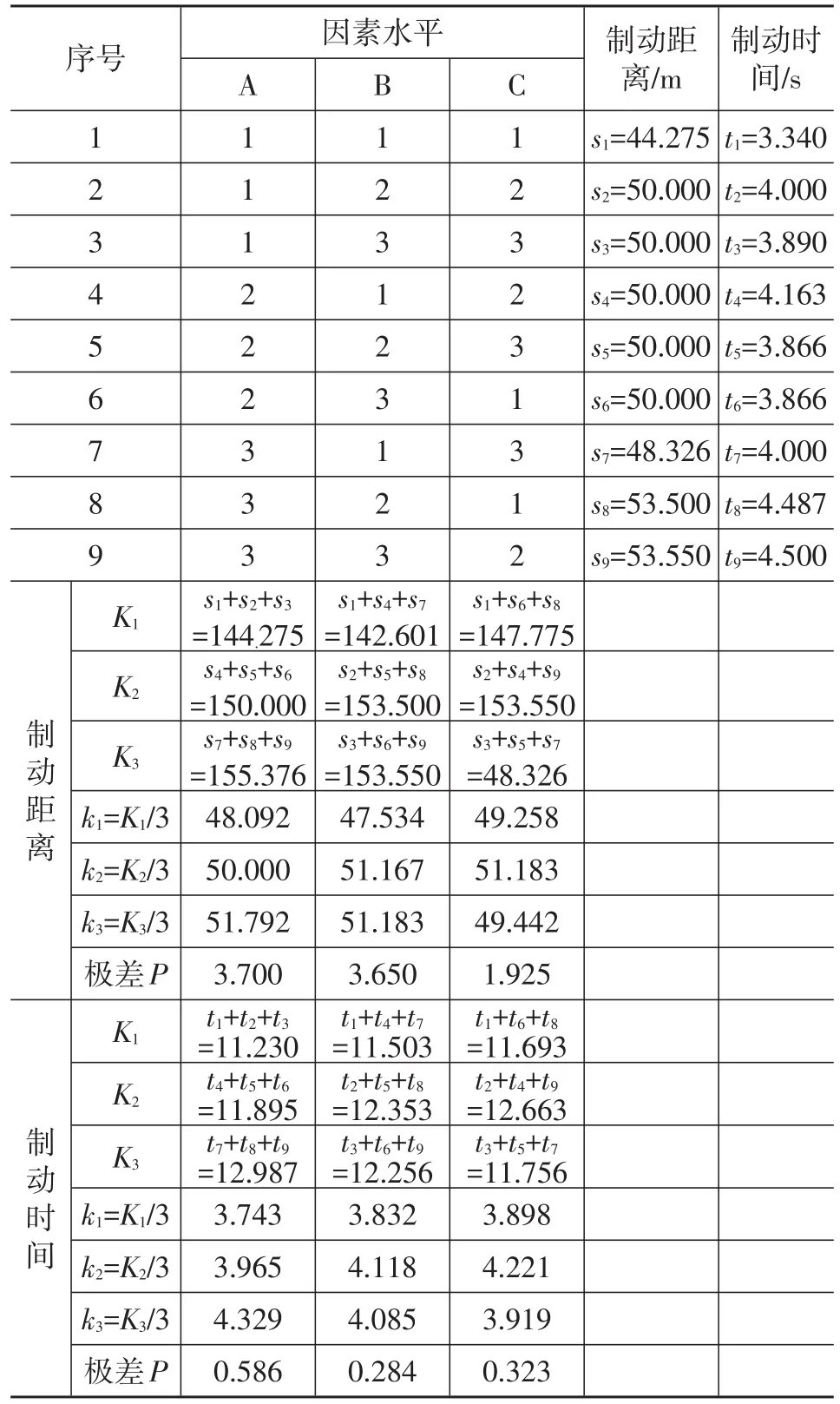
表4 試驗設計方案及結果

極差P為k1、k2、k3中最大值與最小值的差值。極差越大，表明因素對試驗結果的影響越大。根據對各因素的極差分析（見表4），可以得到以下結論：

a.角減速度門限值對制動距離和制動時間來說，極差均較大，是影響控制效果的關鍵因素。

b.以制動時間作為考察指標，滑移率門限值的極差與角加速度門限值的極差相差不大；以制動距離作為考察指標，滑移率門限值的極差遠大于角加速度門限值的極差。因此，滑移率門限值是影響控制效果的次要因素。

c.角加速度門限值對兩個指標的極差都較小，是對控制效果影響最小的因素。

利用SPSS軟件實現正交設計的方差分析，結果如表5和表6所示，由表5、表6可得各因素之間的顯著性差異。F值是均方與自由度的比值，可以作為反映顯著性差異的參數。F值越大，表明因素對試驗結果的影響越大。對制動距離來說，FB＞FA＞FC，即滑移率門限值對制動距離的影響最大；對制動時間來說，FA＞FC＞FB，即角減速度門限值對制動時間的影響最大。綜合表4～表6可得，3個因素對控制效果的影響由大到小依次是：角減速度門限值、滑移率門限值、角加速度門限值。

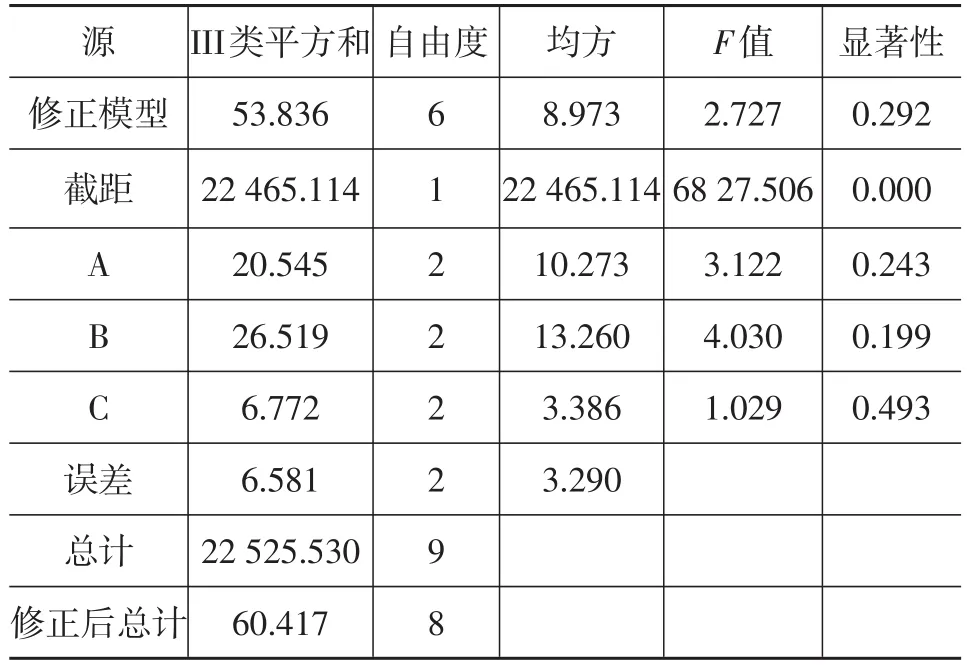
表5 SPSS的制動距離方差分析

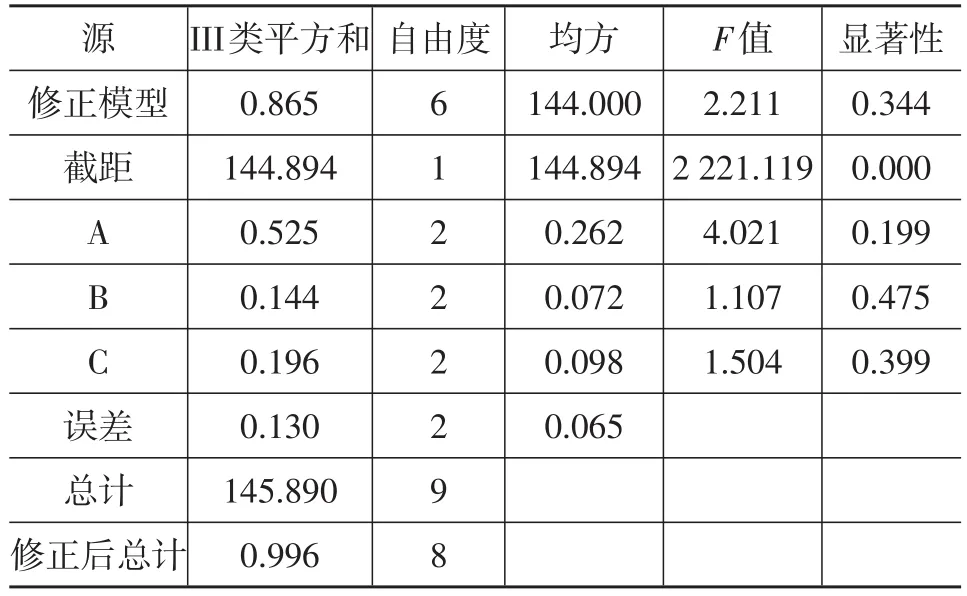
表6 SPSS的制動時間方差分析

在確定了顯著性差異的情況下，可根據趨勢圖確定最佳門限值。在SPSS軟件的Data View視圖中輸入L9(33)正交表和9個試驗指標的試驗結果，得到各因素水平趨勢如圖3所示。

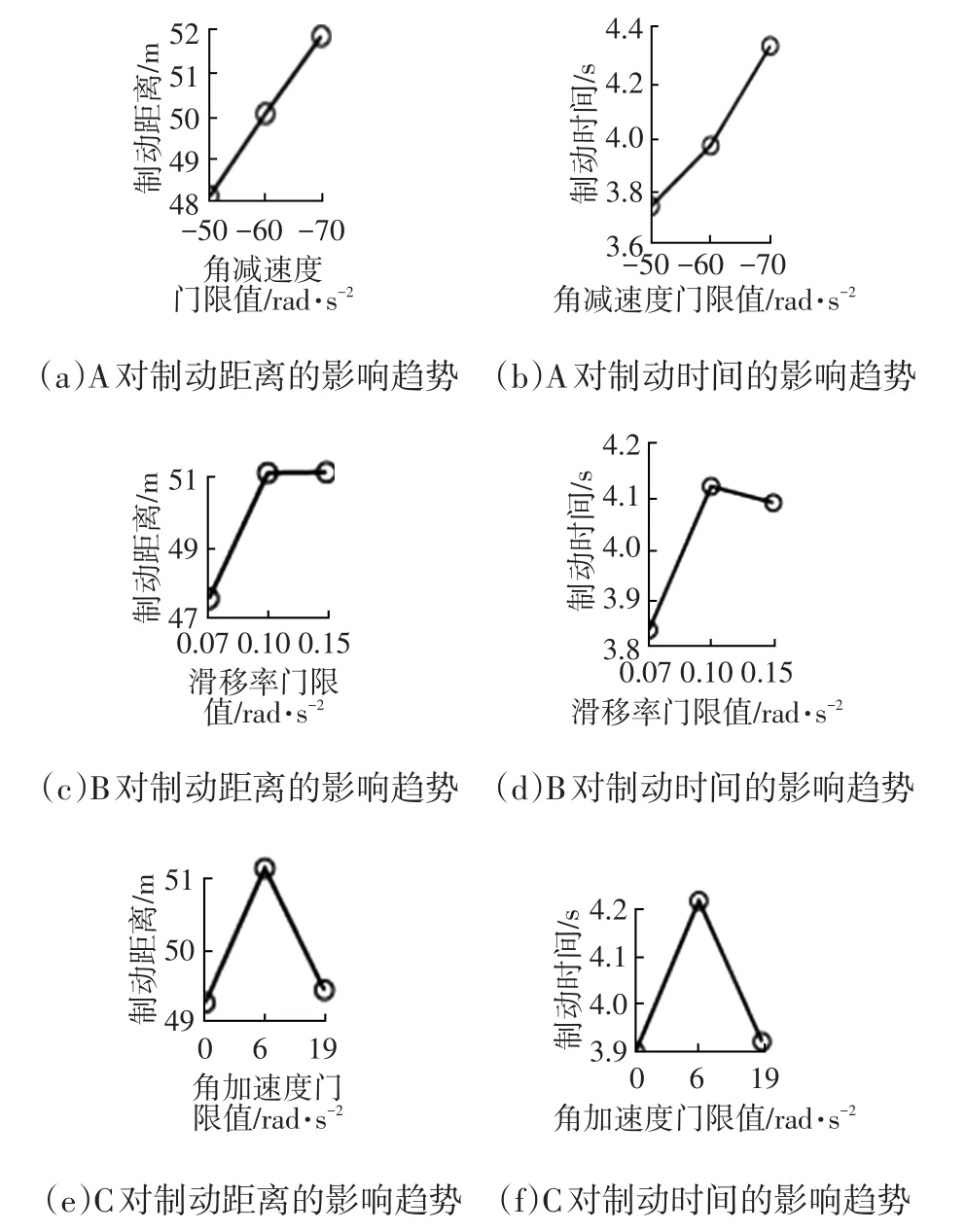
圖3 影響制動距離和制動時間的各因素水平趨勢

圖3所示為正交試驗中各因素各個水平平均值的趨勢。對于制動距離和制動時間，其值越小代表車輛的制動性能越好。由圖3a、圖3b可知，制動距離和制動時間隨著門限值的減小而顯著增大，即角減速度門限值A取-50 rad/s2時制動距離和制動時間為最小；由圖3c、圖3d可知，制動距離和制動時間隨著門限值的減小先增大后小幅減小，即滑移率門限值取0.15時制動距離和制動時間最小；由圖3e、圖3f可知，雖然制動距離和制動時間隨著門限值的減小先水平增大后大幅減小，角加速度門限值C取0和19 rad/s2時制動距離和制動時間相差不大，但角加速度門限值C取0時，輪速還未完全恢復就進入增壓狀態，會導致車輪過早抱死。根據表4可以確定各水平代表的最佳門限值組合為A1B3C3，即角減速度門限值為-50 rad/s2、滑移率門限值為0.15、角加速度門限值為19 rad/s2。

3 仿真平臺搭建

3.1 整車動力學方程

本文重點研究輪轂電機驅動電動汽車的防抱死制動系統，因此忽略懸架特性，搭建包括車輛、車輪、輪胎等模塊的7自由度整車模型，其方程如下：

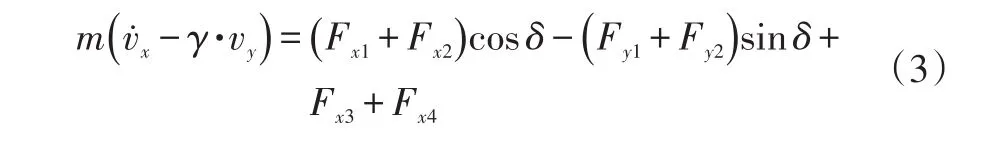
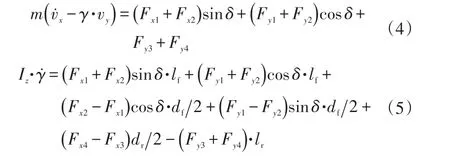
式中，m為整車質量；vx、vy分別為整車沿車輛坐標系x、y軸的分速度；v為車速；γ為整車橫擺角速度；Fxi、Fyi分別為輪胎縱向力、側向力，i=1,2,3,4分別表示左前輪、右前輪、左后輪、右后輪；δ為前輪轉角；Iz為車輛繞Z軸的轉動慣量；lf、lr分別為前、后軸到車輛質心的距離；l為軸距；df為前軸輪距；dr為后軸輪距。

3.2 車輪動力學方程

4個車輪的力矩平衡方程為：

式中，Tb為制動器制動力矩；Fxb為地面制動力。

車輛轉向時，縱、橫向加速度分別為：

輪胎的垂向載荷為：

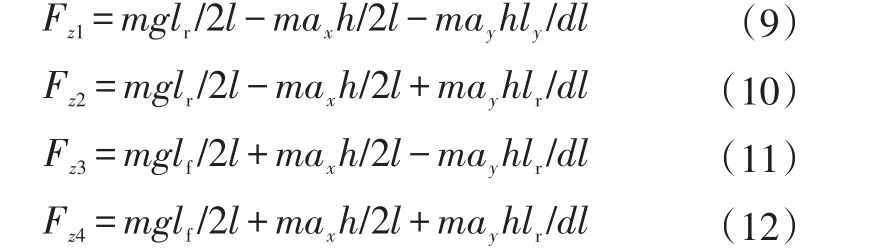
式中，Fzi(i=1,2,3,4)為各車輪垂直載荷；h為質心高度。

各車輪輪胎的側偏角αi為：

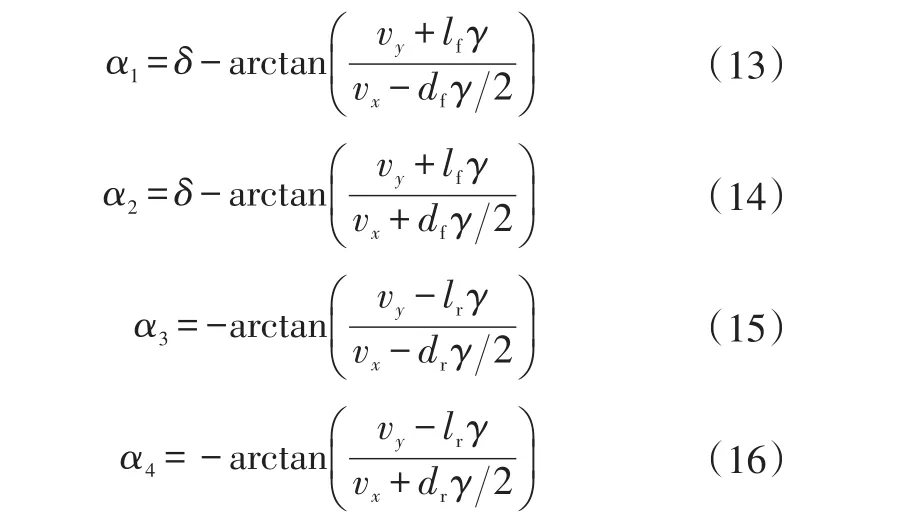
各輪輪心在車輪坐標系下的縱向速度vti為：

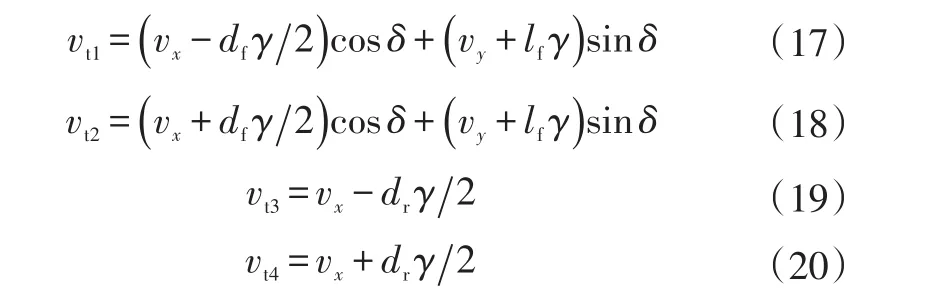
輪胎滑移率可表示為：

式中，ω為車輪角速度。

本文所研究車輛的基本參數如表7所示。

表7 整車性能參數

4 仿真分析

4.1 車輪轉動慣量增加對門限值的影響

本文以角減速門限值為例進行分析。由車輪運動方程可知，除地面制動力矩和制動器制動力矩外，車輪轉動慣量也是影響車輪運動特性的重要因素。通過對無ABS的單輪車輛模型進行仿真，可得到不同車輪轉動慣量下的角減速度曲線，對比峰值縱向力時刻的角減速度及其對應的時間，可得到車輪轉動慣量增加對減速度門限值的影響規律，如表8所示。由表8可知，車輪轉動慣量對角減速度門限值靜特性無影響，對其動特性影響較大。具體表現為，車輪轉動慣量越大，角減速度門限值越小，達到峰值縱向力的時間越長。因為車輪轉動慣量越大，系統的慣性越大，車輛保持原行駛狀態的能力越強，車輪對制動壓力的反應越遲鈍，車輪角速度變化率低，即角加/減速度小。在門限值相同的條件下，車輪轉動慣量較小時，車輪角減速度能在滑移率到達最佳滑移率前達到門限值，車輪轉動慣量較大時，車輪角速度變化率低，車輪減速度達不到門限值，而當車輪到達最佳滑移率時已經處于不穩定區域，很容易發生抱死。因此，車輪轉動慣量較大時應減小角減速度門限值。

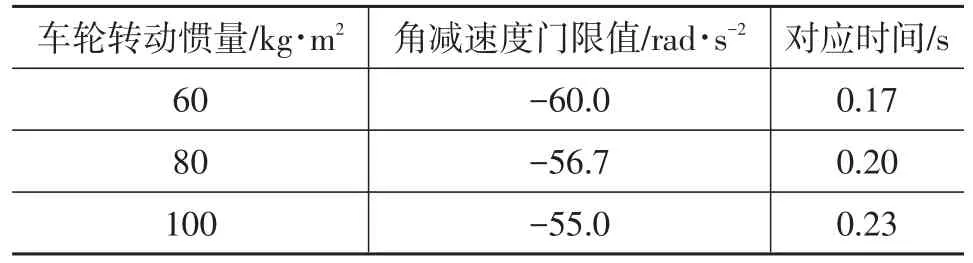
表8 不同車輪轉動慣量下的角減速度門限值

4.2 車輪轉動慣量增加時的仿真分析

為了研究車輪轉動慣量增加對ABS控制邏輯的影響，在采用傳統汽車ABS控制邏輯的前提下，對不同車輪轉動慣量的情況進行了對比分析，制動初速度為90 km/h，仿真結果如圖4所示。

從圖4可以看出，隨著轉動慣量的增加，車輛制動性能下降，具體表現為：車輪轉動慣量為2 kg·m2和1.5 kg·m2條件下，相比 1.2 kg·m2時的制動距離分別增加了4 m和2 m，制動時間分別增加了0.2 s和0.1 s。

基于本文的分析方法，調整門限值后，仿真結果如圖5所示。

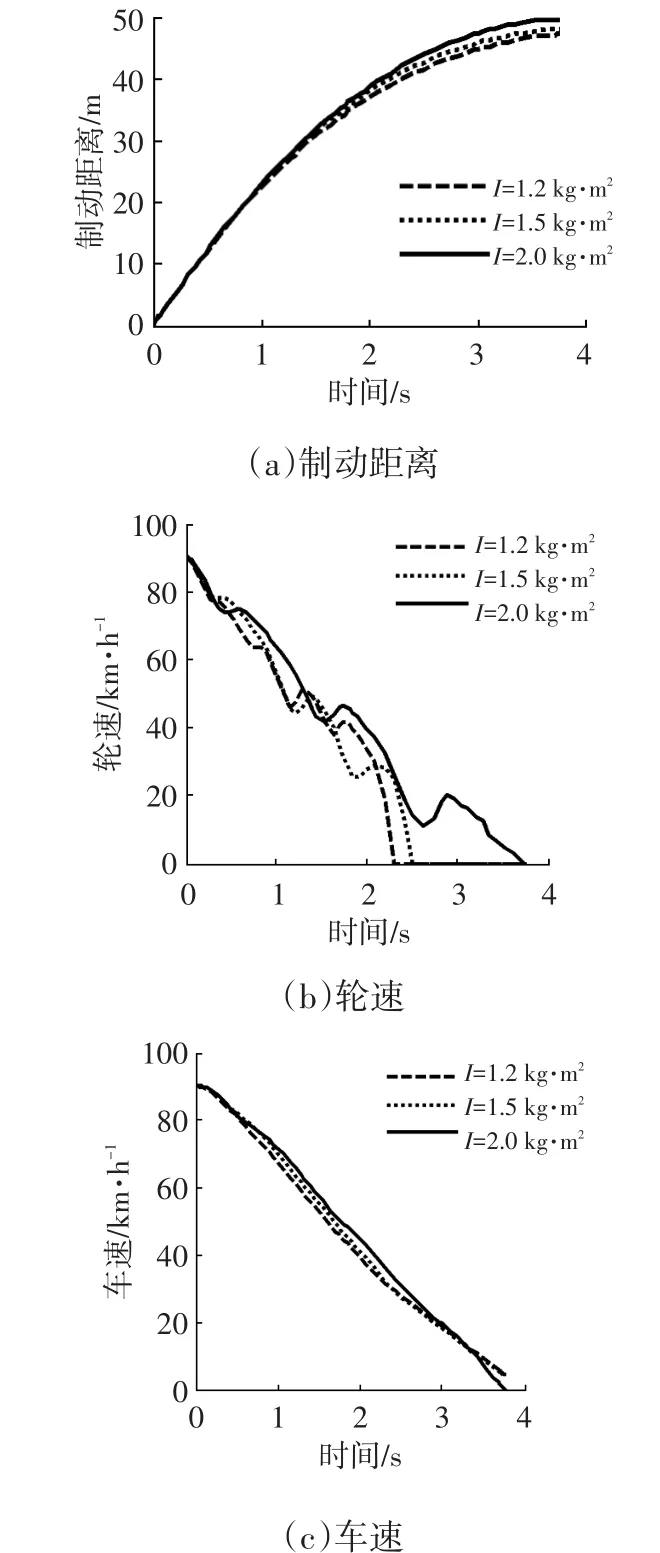
圖4 不同車輪轉動慣量下的制動距離、輪速和車速

從圖5可以看出，不同車輪轉動慣量條件下，門限值調整后，制動距離最大縮短了5 m，制動時間減少了0.15 s，制動性能得到明顯提升。

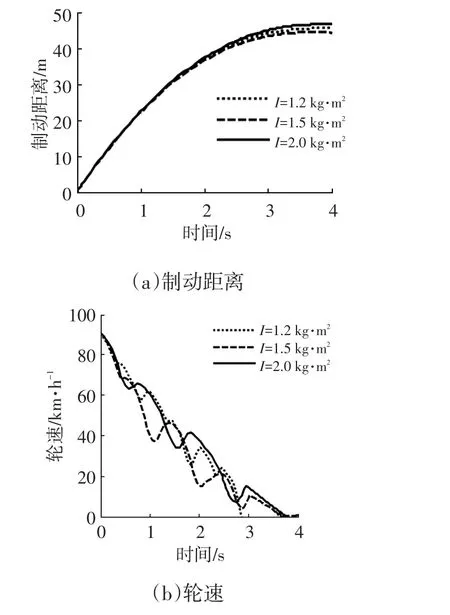
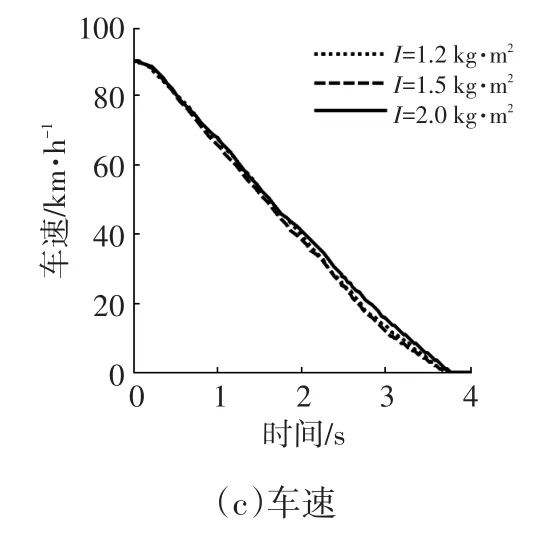
圖5 調整門限值后的制動距離、輪速和車速

5 結束語

本文基于MATLAB/Stateflow搭建了一種以車輪角減速度為主要控制參數、以滑移率為輔助控制參數的邏輯門限值ABS控制模型，利用正交試驗及方差分析得到了門限值對ABS影響的顯著性差異并確定了最佳門限值。仿真結果表明，所提出的邏輯門限控制算法能夠很好地解決由車輪轉動慣量增加帶來的主動安全性問題，使整車制動性能顯著提升。