“構造逆命題”在初中幾何圖形的判定教學中的應用

江蘇省昆山市城北中學 金小丹

數(shù)學學習中，處處有命題，在很多情況下，我們可以通過對調(diào)原命題的條件和結(jié)論來構造原命題的逆命題，從而獲得新知識。初中幾何中同一知識對象的性質(zhì)定理與判定定理往往是互逆的，如平行線的性質(zhì)與判定、平行四邊形的性質(zhì)與判定等。本文就幾何圖形判定定理的教學為例做分析，探討如何利用矩形、菱形的性質(zhì)定理構造逆命題來學習矩形、菱形的判定定理。以此為基礎，結(jié)合“直角三角形斜邊上的中線等于斜邊的一半”的逆命題闡述如何引導學生獲得新知。

一、從矩形、菱形的性質(zhì)定理到矩形、菱形的判定定理

學習矩形、菱形的判定定理前，學生已經(jīng)學習了性質(zhì)定理，因此，可以將性質(zhì)定理確定為新知識的生長點，引導學生逆過來思考，即構造性質(zhì)定理的逆命題，加以證明或修正，從而主動獲得矩形、菱形的判定定理。

先以矩形判定定理教學為例，學生已經(jīng)學習了矩形的性質(zhì)定理——矩形的四個角都是直角，對角線相等。上課之初，我讓學生分別寫出以上兩個命題的逆命題——“四個角都是直角的四邊形是矩形”“對角線相等的四邊形是矩形”。

對于第一個命題，“四個角都是直角的四邊形是矩形”，這是真命題。我引導學生思考是否需要四個角都是直角，學生意識到存在多余條件，可以修改為 “三個角都是直角的四邊形是矩形”，接著畫出圖形，運用矩形的定義進行證明。

已知：在四邊形ABCD中，∠A＝∠B＝∠D＝90°，求證：四邊形ABCD是矩形。

證明：∵∠A＝∠B＝∠D＝90°，

∴∠A+∠B＝180°，∠A+∠D＝180°，

∴AD∥BC，AB∥DC，

∴四邊形ABCD是平行四邊形，

又∵∠A＝90°，∴四邊形ABCD是矩形。

經(jīng)過證明，這個命題是真命題，于是得到判定定理——“三個角是直角的四邊形是矩形”。

對于第二個命題，“對角線相等的四邊形是矩形”，學生很快判斷這是個假命題，并且舉出反例——等腰梯形。接下來自然產(chǎn)生疑問：“這個命題如何修改可以得到一個真命題？”經(jīng)過短暫思考，學生給出答案，將“四邊形”改為“平行四邊形”，即“對角線相等的平行四邊形是矩形”。

在根據(jù)矩形的定義證明這個命題時，學生提出可以通過三對邊對應相等證明圖中△ABD與△DCA全等，從而得到∠BAD與∠CDA的等量關系，又由平行四邊形對邊平行可得AB∥DC，從而∠BAD與∠CDA互補，因此∠BAD與∠CDA都等于90°，根據(jù)矩形的定義可證得四邊形ABCD是矩形。具體證明過程如下：

已知：如圖1，在ABCD中，AC=BD。求證：ABCD是矩形。

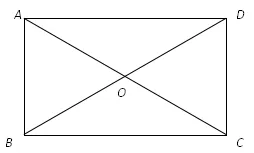
圖1

證明：∵四邊形ABCD是平行四邊形，

∴AB∥DC，AB=DC。

∵AB=DC，AD=AD,BD=AC，

∴△ABD與≌△DCA（SSS）。

∴∠BAD=∠CDA。

∵AB∥DC，∴∠BAD+∠CDA＝180°，

∴∠BAD=∠CDA=90°，∴平行四邊形ABCD是矩形。

經(jīng)過證明，這個命題是真命題，于是得到判定定理——“對角線相等的平行四邊形是矩形”。在探索矩形的判定定理教學過程中，以學生已有的矩形的性質(zhì)為知識生長點，通過構造逆命題來獲得矩形的判定定理，這符合新的建構主義思想：教學應當把學習者原有的知識經(jīng)驗作為新知識的生長點，引導學習者從原有的知識經(jīng)驗中生長新的知識經(jīng)驗。

學習菱形的判定方法時，同樣的方法，讓學生寫出菱形的兩個性質(zhì)“菱形的四條邊相等，對角線互相垂直”的逆命題，進而通過證明命題或者對命題進行修改使之成為真命題，從而得到菱形的判定定理“四邊相等的四邊形是菱形”“對角線互相垂直的平行四邊形是菱形”。

因為探索矩形或菱形的判定方法是建立在學生已有的知識經(jīng)驗基礎之上的，學生對于矩形、菱形的性質(zhì)并不陌生，只是將性質(zhì)定理改寫為逆命題并合理修改并證明，使之成為真命題，所以整個教學過程都是在教師的引導下自然進行的，學生積極參與到學習中來，凸顯了學生的主體地位，做到了“將課堂還給學生”。

二、從直角三角形斜邊中線定理到逆命題

直角三角形是初中幾何中一種重要的圖形，斜邊上的中線定理是常考常用的一個定理。這個定理沒有逆定理，但是它的逆命題在判斷一個三角形的形狀時會經(jīng)常出現(xiàn)，因此，在學習了定理“直角三角形斜邊上的中線等于斜邊的一半”之后，我讓學生寫出這個命題的逆命題“在一個三角形中，如果一條邊上的中線等于這條邊的一半，那么這個三角形是直角三角形”并判斷其真假。

學生通過舉例猜想這是個真命題，之后通過幾何證明驗證了猜想。

圖2

分析：要證明∠ACB＝90°，就是要證明∠ACD+∠BCD＝90°。由條件可知AD=BD=CD，則∠A＝∠ACD,∠B＝∠BCD，所以∠ACD+∠BCD= 內(nèi)角和的一半。

證明：在△ABC中，

∵CD是AB邊上的中線，∴AD=BD=AB。

∵CD＝AB，∴AD=BD=CD，

∴∠A＝∠ACD,∠B＝∠BCD，

∵∠A+∠ACD+∠B+∠BCD=180°，

∴∠ACD+∠BCD=90°，

即∠ACB＝90°，∴△ABC是直角三角形。

經(jīng)過證明，學生對這個命題有了深入的領悟，之后通過系列練習，學生提出 “如果一個三角形一邊上的中線將這個三角形分成了兩個等腰三角形，那么這個三角形是等腰三角形”也是個真命題。

三、小結(jié)與思考

數(shù)學學習中處處有命題，處處有新知，“授人以魚不如授人以漁”，如何發(fā)揮學生的自主性，主動獲得新知識，這是每位教育工作者都會思考的問題。學生的知識體系是不斷充實的，如果能利用學生已有的知識體系，找準知識生長點，加以適當?shù)囊龑В寣W生自主學習，將起到事半功倍的效果。