“深度學習”視角下的教學案例研究
——以溫度計為載體實現負數雙向認知

吳緒益（特級教師）

【教學內容】

北師大版四年級上冊第七單元生活中的負數之《溫度》。

【課前思考】

一、了解前世，啟迪今生

世界各國對負數的認識和接受有一個過程。中國是世界上最早應用正負數的國家，早在兩千多年前的《九章算術》中，就有正數和負數的記載，在古代人民生活中，以收入錢為正，以支出錢為負；在糧食生產中，以產量增加為正，以糧食減少為負。西方國家認識正負數要比中國晚數百年。（存在的必要性）

1484年法國數學家曾得到方程的一個負數解，但是他不承認，說負數是荒謬的數。1545年卡爾丹承認方程的負數解，但認為是“假數”，到1831年還有數學家認為負數是虛構的，并舉出一個特例：父親56 歲，兒子29 歲，問什么時候父親歲數是兒子的兩倍？用方程解出x=-2 他認為這是一個荒唐的數。（接受的長期性）

負數是抽象的存在，比0 還小的數，有嗎？比沒有還少，這是多么難以理解。如何讓不可思議的假數變得觸手可及？如何實現數與形結合？利用溫度計將抽象變得直觀。（學生認知困難性）

二、文獻研讀，把握本質

1.課標研讀。

《數學課程標準（2011年版）》中對負數的要求：在熟悉的生活情境中，了解負數的意義，會用負數表示日常生活中的一些量。

《數學課程標準（2011年版）》解讀：負數的引入是數的概念的進一步擴充，根據小學生的思維發展水平，只是在第二學段對負數提出簡單的要求。對于小學生來講，理解負數的意義是有一定難度的。第一，限定在了解的層次。第二在具體的情境中了解。如用溫度的變化來體會負數，零度以上用正數表示，零度以下用負數表示。（教學達成度）

2.教學法研讀。

《數學教學論》（曹一鳴主編）中說：數學概念的特點是具有高度的概括性和抽象性。數學概念包括五個方面：名稱、定義、符號、例子和屬性。數學概念具有一定的系統結構。數學是一個有機的整體，數學概念是隨著數學知識的發展而不斷發展的，學習數學概念也要在數學知識體系中不斷加深認識。要瞻前顧后，實時強調該內容與其他內容的聯系，促進學生不斷從新的角度理解原來的知識，對認知結構進行調整和重新組織。從數學概念之間的關系來學習概念，可以深化對所學概念的認識，有利于加深對有關概念的理解，也便于學生記憶。新概念的引入一般分為兩類：一類是從數學體系的發展過程中引入新概念，另一類從解決實際問題的需要出發引入新概念。（概念學習的基本規律）

三、教材對比，提升認知

1.蘇教版教材編寫意圖。

例1（溫度）：現實情境引入負數。

（1）氣溫是學生每天生活中能夠接觸到的信息，對此他們并不陌生。

（2）借助溫度計的數據顯示，可以直觀地認識到零上溫度比零攝氏度高，零下溫度比零攝氏度低。這些為學生初步了解正負數表示具有相反意義的量提供了直觀形象的模型。

2.北師大版教材編寫意圖。

（1）在天氣預報中，學生經歷并創造了用符號或圖形表示零上溫度和零下溫度，并溝通了多種表示方法之間的聯系，優化用符號表示的方法，產生了用負數表示的現實需求。

（2）在從溫度計中認、讀、找溫度的過程中，學生很直觀地感受負數的意義，比較零上溫度與零下溫度之間的高低，初步擴充對數的認識等。

（3）引導學生結合溫度的生活經驗，對帶符號的溫度進行比較。

由此看來，兩個版本的教材都采用了把溫度計作為認識負數的直觀現實模型。在溫度計上體會負數的含義，并進行負數大小的直觀比較。

四、學生現狀，教學起點

在《科學》（教科版）三年級下冊教材中《溫度與溫度計》一課中，學生應該了解溫度計的用途、如何工作、如何識讀。而本課的要旨不在于溫度本身，而是把溫度作為研究的背景，初步體會相反意義的量。《科學》在先，《數學》在后。在科學課上對于溫度表示的方法是告知的方式；而數學課應該讓他們感受這種表示方法的必要性。

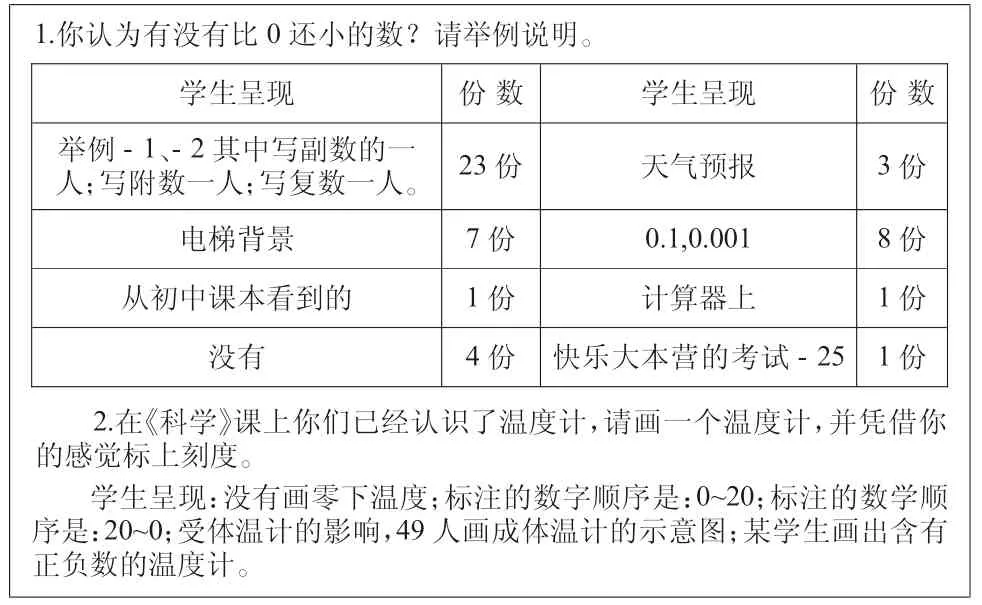
前測結果統計：

啟示：1.學生知道有比0 還小的數，但是不明白含義（附、復和副可以推知）。2.學生對負數出現的現實背景是豐富的（電梯、天氣預報、計算器、考試得分）。3.對于把小數看成比0 小的數，確實令人擔憂。（說明對于小數本質的認識不到位）4.很多學生對溫度計的認識停留在體溫計的認知層面上。

【教學過程】

一、情境導入，引入負數

1．讀文字感受相反。

師：同學們請看下面兩段文字，誰能把它深情地朗讀一下？

李老板辛苦奮斗一年賺了100 萬塊錢。

王老板辛苦奮斗一年虧了100 萬塊錢。

（讀第二句學生大笑）

師：你的笑背后有含義嗎？

生：一個賺100 萬，一個是虧100 萬。

師：這兩個100 萬一樣嗎？為什么？

生：不一樣，100 萬的數量是一樣的，但是一個是虧了。

師：同樣是100 萬，如何把“虧”和“賺”區分開呢？接下來把時間交給你們，請你們創造一個表達的方法，讓別人一眼看出兩者的不同。

學生獨立創造，一位學生展示并解讀自己的創造：+100 萬，-100 萬。

師：這兩個100 萬有什么不同？

生：-100 萬在賬單中表示的是欠100 萬。

師：“-”這個符號以前見過嗎？

生：在溫度計中見過的。

師：（呈現三種不同的表達方式）你能看懂他們的表達方式嗎？

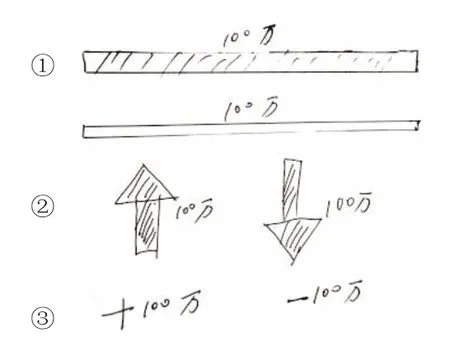
師：在這三種方式中你最喜歡哪一種表達方式？

生：第③種，因為第③種簡潔。

2.生活經驗感知相反。

師：同學們，帶著對符號的美好感覺，讓我們一起來走近周末的霍山天氣。

（PPT 呈現霍山周末溫度）

學生齊讀溫度。（霍山：最高零上3 攝氏度，最低零下3 攝氏度）

師：這兩個3 攝氏度一樣嗎？哪里不一樣？

生：不一樣。第一個是零上，第二個是零下。

師：請將這兩個不同的溫度用數學符號區分開。

（學生板演：+3℃，-3℃）

教師引導觀察并總結：這樣就將兩者區分開，數學真的很好，用簡單的符號表達不同的數學含義。（同時介紹了攝氏度的書寫以及攝氏度的由來即為了紀念瑞典著名的天文學家攝爾修斯取第一個字母C）

二、深度探索，建構模型

師：請同學們在溫度計上找出+3℃的位置。

師：（從學生中選出兩幅不同的作品）什么原因造成一個3 在上，一個3 在下。

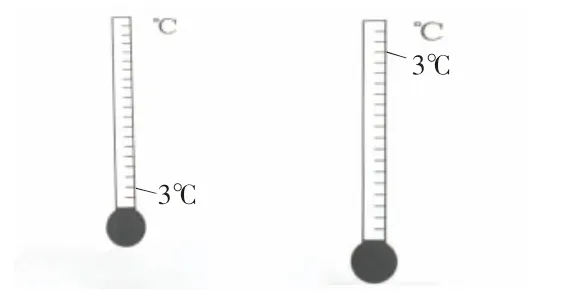
生：中間沒有標出0。

師：看來，0 的位置很重要。（教師順手在黑板上標出0 攝氏度的位置）

（請一位學生在黑板上標出+3℃的位置）

（全體學生一起數出+3℃的位置。讓更多的學生體會+3℃的位置的由來）

師：-3℃在什么地方？

（全班一起數出-3℃的位置，關注讀法、寫法、位置）

師：接下來讓我們一起來感受溫度的變化。氣象學家發現溫度從中午的12 點開始每2 個小時大概下降1 攝氏度。如果此時此刻是3℃，那么2 個小時之后是多少攝氏度？

生：2℃。

師：哪位同學能夠用算式表達這個降溫的過程？

生：3℃-1℃=2℃。

師：如果又過了2 個小時，此時的溫度是多少？

以此類推：2℃-1℃=1℃ 1℃-1℃=0℃

師：（當學生寫出：0℃-1℃= 的時候）停！此時此刻減的結果是多少？

生：（指著溫度計齊說）-1℃。

生：-1℃-（-1℃）=-2℃。

師：這個算式是表達繼續降溫1 攝氏度嗎？

生：錯的，減1 攝氏度，不是減零下1 攝氏度。

生：-2℃-1℃=-3℃。

師：同學們帶著對溫度的美好感覺，請幫助吳老師選擇衣服以便我元旦進行旅行。

出示：漠河、西安、臺北三地不同的氣溫。

師：同學們對溫度的感覺真好，下面把目光投向大屏幕，仔細觀察溫度計上這些數字如何變化的？（動態演示以0 為起點，零上溫度與零下溫度向兩邊不斷發展，形成數軸）

生：零上溫度逐漸上升。

生：零下溫度逐漸下降。

三、計算推理，打通關聯

再次把學生的目光引向算式，此時此刻教師把帶有攝氏度的符號擦去形成：

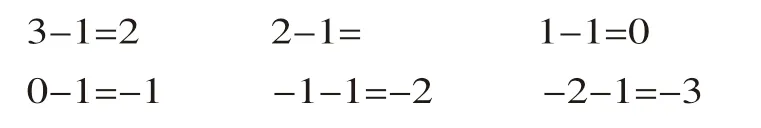
師：請仔細觀察第一排的算式有什么特點？

生：攝氏度沒有了。

師：這樣的算式你在什么地方見過？

生：一年級。

生：第一排算式是大數減去小數。

師：再仔細觀察第二排，你發現了什么？

生：0-1，0 減不了1 呀！

師：老師再次把攝氏度的符號寫上。

生：第二排算式是小數減去大數。

師：你們長本領了，不知不覺中用小數減去大數產生了負數。數學就是這樣充滿著奧秘與神奇。其實在數的發展過程中，負數只是其中的一分子。從此以后（出示橫放的數軸），我們的數軸也由原來的射線變成一條直線。當然這些都不是終點，隨著學習的深入，數的家庭還將增添新的成員，讓我們共同期待。

四、全課小結，自然延伸

1.進行選詞填空：副數 附數 負數

2.到黑板上圈出給你留下印象最深的地方。

【課后反思】

一、充分發揮溫度計的數學作用

1.溫度計直觀模型沒有標出0℃的位置，讓學生在認知沖突中體悟分界點的重要作用。

2.以溫度計作為載體進行減法計算，在去除攝氏度符號以后實現減法計算的封閉性，讓學生體悟到負數的產生順理成章。

二、把握數學本質，實現深度學習

1. 導入環節突出負數的核心本質——數量相等，意義相反。人民幣的收支個人體驗要好于溫度的體驗，學生在對比研讀的時候感到有趣，同時體驗負數產生的必要性。

2.差異是深度學習的重要資源。教師首先應尊重差異，努力構建開放型的數學課堂。有的放矢地傾聽差異、引導差異、點撥差異、放大差異、糾偏差異，讓數學課堂飛得更高即站在兒童立場上進行數學教學。

3.教學不僅要關注學生學到多少，而且要關注學生在學習的道路上走多遠。教師要做到對教學內容的高屋建瓴，對數學教育的理解高站位，基于對數學內涵的深度開掘，關注知識的前世今生，這樣教學內容也將更加豐滿，為學生的思維提供一個廣闊的學習背景，激發他們深度的思考。突出知識的架構，打通彼此的關聯。讓數學的味道更濃一些，以數學學科的力量助推學生核心素養的提升。

三、課后訪談，啟示未來

課后對學生進行了深度訪談發現：1.對零下溫度大小的比較僅僅依賴于課中的三次滲透（選擇衣服、觀察溫度計上的數據規律、減法計算）可能不夠明晰。2.對正號的省略沒有說明，致使部分學生對省略以后的數不認同是正數。

綜上所述，要想讓學生深度地學習，教師需要深度地教。抓住數學本質，利用溫度計的直觀模型實現負數的雙向認知即從現實背景和數學發展內部兩個角度來認識負數。不可否認學生對負數的認識僅僅依賴一節課教學是遠遠不夠的，因為教育是慢的藝術，但是作為小學數學教師可以為他們埋下負數認知的種子。