高中數學最值問題教學困境與突圍之道分析
江蘇省無錫市第三高級中學 高守家
數學最值問題存在于整個高中教材。通過了解實踐教學案例可知,不管是三角函數,還是不等式、數列等模塊包含的最值問題,都具有復雜性和多樣性。因此,教師要想提升相關內容的教學效率,優化學生的解題水平,就要深層探索最值問題的解決方法,并對最值問題進行分類分析,以此針對不同類型的最值問題提出有效的解決方法。下面對高中數學最值問題進行研究。
一、二次函數的最值問題及解析
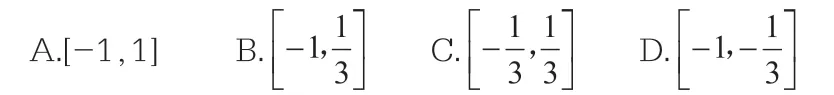

此時,令t=cosx,且t∈[-1,1],
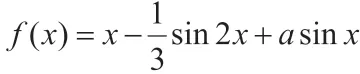
二、不等式的最值問題及解析
很多情況下,學生可以通過觀察考試試卷發現,不等式恒成立問題一直都是他們學習的重難點,此時教師要想提升學生解題水平,減少問題的出現,要針對學生的薄弱環節進行分析。下面利用基本不等式分析求最值的技巧。例如,大部分學生會引用常數代換法進行問題解析,雖然這種方法操作起來非常簡單,但會有一定誤區,下面對例題進行分析:
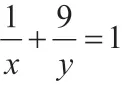
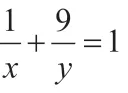
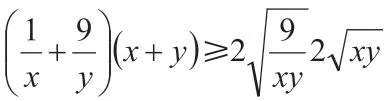
因此,最終可得x+y的最大值是12。
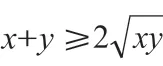
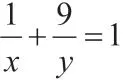
三、三角函數的最值問題及解析
對三角函數來說,教師結合自己的工作經驗分析可知,可以引用多種方法解決其提出的最值問題,其中最常見的就是數形結合法。下面結合具體例題進行問題分析。
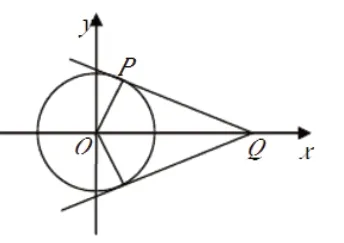
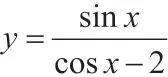
四、數列中的最值問題及解析
數列作為定義域是正整數的離散函數,不僅具備函數的性質,還擁有自己的獨特性。高中教師整理以往教學經驗可以發現,教師針對數列提出的最值問題主要分為三種:其一,求得數列的最大項和最小項;其二,求解等差數列的前n項和的最值;其三,數列中的恒成立問題。下面結合具體案例進行問題解析:
例4:已知數列{an}中,(n∈N+,a∈R,且a≠0)。
(1)若a=-7,求數列中最大項和最小項的值;
(2)若對任意n∈N+,都有an≤a6成立,求a的取值范圍。
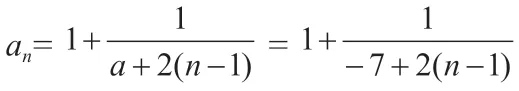
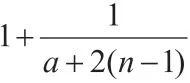
綜上所述,為了讓學生可以更快地理解和應用最值問題,高中數學教師要在引導學生解題的過程中強化他們的數學思維,并指導他們構建解題的自信心,進而依據引用科學的解題方法,幫助學生更快掌握和理解最值的有關知識點,以此在考試中獲取優異成績。同時,在新課改下,教師要調動學生自主探索的積極性,促使他們可以更快地計算最值問題。

