構造法及其在高中數學解題教學中的應用
江蘇省如皋中學 胡志軍
數學科目都是必修的科目,直接影響了學生的高考成績。因此應當學習更加高效的數學解題方法,有效提升高中生解題速率的同時也提升了數學成績。構造法指的是為了有效地解決數學問題,從而構造的一種新型的解題方法,主要是通過借助圖形、公式、方程還有函數之間的應用關系來有效利用構造法,尋找結構與問題之間的深層化聯系,由此來達到簡化的求解過程,從而進一步地轉換數學思維等多種目的。數學構造法主要包括了類比以及推理、化歸等多種思維形式,可以很好地解決高中數學問題。構造法可以更加積極有效地將高中數學問題得以解決,因此在解答高中數學題目時通過引入構造法,可以很大程度地提高高中數學的解題效率。
一、數式模型的構造
數學是高中課程中的重要組成,運算更是高中數學課程中尤為重要的內容。那么解決某種數學問題的過程中,可以有效地通過觀察題目、分析題目中的題設以及題目結論中所存在的諸多關聯性,繼而引入構造法來構造出新型的數學模型,有效地解決了問題。
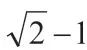
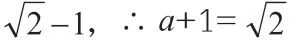
二、函數模型的構造
在高中數學課程的開展解題過程中,函數是重要的組成部分,覆蓋了較廣的高中數學知識點,并且涉及了較多的數學內容。比如一次函數、二次函數以及指數函數、冪函數,還有反比例、對數函數和三角函數等。在對數學問題的解題過程中,通過分析題設,以及結論來利用構造法,構造出一種新型的函數模型,由此較為簡便快捷地將問題得以解決。通過對函數問題解決時整體利用構造法,此種過程是一種思維創造性的過程,將整個解題過程變得更具備技巧靈活性。因此使用此種構造法完成函數數學題目解答過程中,應當構造題目的解答目的以及下意識地進行條件構造,并且要始終重視要證以及解題目標。
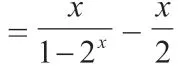
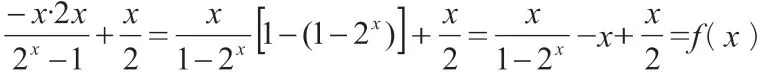
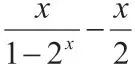
三、方程模型構造
在高中數學題的解題過程中,方程也是數學題目的重要內容,方程更是與函數之間存在著尤為緊密的聯系性。因此在對數學的方程模型進行解題的過程中,可以依照具體的題設來完成方程的構造,從而將方程的復雜問題轉換成為方程,進而使用方程的方法得以解決。
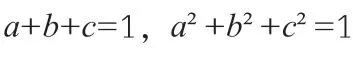
解:∵a+b+c=1,∴a+b=1-c①
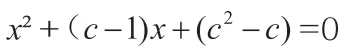
四、向量構造法
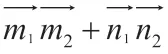
五、解析式構造法
解析式構造法的使用實際可以經過完成適當關系的合理構建,來起到題目解答的輔助性作用。在解題過程中通過使用此種適當的關系式,可以很大程度地將學生解題的思維完成簡化,并且解析式的構造也應當依照相對應的模型來完成,主要通過將實際性的數學問題特征完成適當關系的合理構建,通過建立的相對應關系式,從而將原本的題干信息進行簡化,有效地解決了原本的數學問題,從而解答數學題目,提升了數學解題速率。
總而言之,通過在高中數學的題目解題中應用構造法,可以有效解答多種題型,并且充分地利用構造法提升解題速率,完成了題目的簡化,提升高中數學解題教學的成效。

