基于Benford-SVR的數據異常檢驗模型構建及其應用

李斐斐 周向陽 秦朗 葛章明 韓書慶 張晶 吳建寨

摘要：當前數據數量劇增的同時，大量異常數據的存在降低了數據質量，數據分析工作面臨著數據豐富而信息貧乏的困境，尋找有效的數據異常檢驗模型，成為數據科學研究的重要內容。本研究以農業生產數據為對象，融合應用Benford定律與SVR模型的技術優勢，構建Benford-SVR異常數據檢驗模型，并以河北省7個地市131個縣為例進行實證分析。結果表明，滄州、邢臺、邯鄲的數據集質量較好，保定、石家莊、唐山、張家口數據集質量較差，并從中有效挖掘出異常較大的數據點。本研究結果為農業數據應用與信息提取提供了參考，Benford-SVR模型可以作為數據質量檢驗中精準挖掘異常點的有效工具。

關鍵詞：數據質量;Benford定律;SVR;農業生產數據

中圖分類號：S126：TP393文獻標識號：A文章編號：1001-4942（2019）07-0136-07

近年來數據資源量劇增的同時，數據質量問題引起了各界高度重視[1]，去冗分類、去粗取精，提高數據質量成為當前主要任務[2，3]。已有研究表明，當前海量數據中不僅存在著許多冗余、缺失、一致性差等問題，還充斥著大量異常數據。這些異常數據并不完全是錯誤數據，而是指數據集中與眾不同的數據，讓人懷疑這些數據并非隨機偏差，而是產生于完全不同的機制[4，5]。基于這種思想，從大數據池中尋找異常數據，提升數據質量，逐漸成為數據科學的一個重要方向，學者們不斷提出基于統計[6]、距離[7]、密度[8]、聚類[9]、BP神經網絡[10]等校驗與挖掘的算法，并應用到經濟、金融、地理、交通等領域。

Benford定律由Simon Newcomb于1881年發現，后在1938年經Benford再次提出引起學術界重視，現已被廣泛應用于異常數據的檢驗中[11]。Benford定律最早被用于網絡入侵[12]、生物生理[13]等自然科學領域數據的檢驗，近年來在會計[14]、統計[15]、財務[16]、保險[17]等社會科學領域的數據檢驗中亦取得了較好效果。Benford定律研究的重點是數據準確性，而非探究數據背后存在的問題。而支持向量機（support vector machine，SVM）能夠攻克“過學習”、“欠學習”、“維數災難”等一些異常數據挖掘中的典型困難[18]，已有研究表明，基于SVM的SVR（support vector regression）模型具備總體殘差較小、魯棒性高的特點，且能有效發現異常數據點[5，19]。

本研究融合兩個模型的優點，構建了Benford-SVR異常數據檢驗模型，并以河北省農業數據進行了實證分析，為數據質量校核及相關研究工作的開展提供支持與參考。

1 材料與方法

1.1 基礎理論

1.1.1 Benford定律 Benford定律也被稱為“首位數定律”，它指出在自然界中數據集中的第一位非零有效整數的統計概率滿足對數分布。在數學上，Benford定律是唯一具有標度不變性的數位定理[20]。Benford定律首數字為1～9的分布概率如公式（1）所示：

由圖1可知，數字1～9在第二位、第三位的概率都是單調遞減的。根據數字的聯合分布函數和乘數法則，可以推導出各數位的條件概率如公式（2）所示：

1.1.2 顯著性檢驗方法 數據的形成受多種外界因素影響，對首位數統計結果進行顯著性檢驗在一定程度上可以避免隨機誤差干擾。假設檢驗的原假設和備擇假設如下：

原假設H0 ：樣本數據集的首位數（更高位數字）統計結果服從Benford定律分布;備擇假設H1：樣本數據集中首位數（更高位數字）統計結果不服從Benford定律分布。

常用的方法有四種：χ2擬合優度檢驗、修正K-S擬合優度檢驗、距離測量檢驗、相關系數檢驗[21]。考慮到統計量受樣本量影響較大，綜合分析各檢驗方法特點，當樣本量不大時，使用χ2、VN對結果進行判定;當樣本量較大時，使用相關系數r對結果進行判定。

表1給出統計量χ2、VN*臨界值情況，其中α表示顯著水平。

（3）Pearson相關系數：是衡量兩個數據集之間相關關系的重要統計量，其判斷標準如表2所示。

1.1.4 核函數 在支持向量回歸過程中，核函數能將原始數據映射到高維特征空間，從而避免原始數據集進行復雜非線性變化時可能發生的“維數災難”，極大提高支持向量回歸效率。核函數變換如圖2所示。

在統計學中，任意滿足Mercer定理的函數都可以作為核函數，從而實現高維映射。常用的有高斯徑向基函數、多項式核函數、Sigmoid核函數、樣條核函數4種，其中，徑向基（RBF）函數可以將數據映射到無窮維，解決大部分支持向量回歸問題[23]，是最常用的核函數之一，具體形式如下：

1.1.5 粒子群算法 核函數中的參數對回歸效果有很大影響，需要用優化算法獲取最優值。常用的優化算法有網格搜索法、遺傳算法和粒子群算法等，其中，粒子群（PSO）算法簡單、搜索速度快、效率高，在求解最優參數過程中具有明顯優勢，應用范圍最廣[24，25]。粒子群算法數學描述為：

1.2 模型構建

綜合利用Benford定律和SVR建立組合模型，其中，SVR模型選取RBF核函數，優化算法采取PSO算法。Benford-SVR模型處理流程如圖3所示。

1.3 數據來源與處理

1.3.1 數據獲取 以農業GDP為分析數據對象，選取2000、2005、2010、2015年河北省石家莊、邯鄲、邢臺、滄州、張家口、唐山、保定7個市131個縣的農業生產數據進行研究。同時，為了試驗準確性，引入農用化肥、農作物總播種面積、農業機械總動力、農業勞動力、有效灌溉面積、農業固定資產投資額等作為關聯驗證數據。數據來源于《中國縣域統計年鑒》。

1.3.2 數據預處理 首先，采用線性插值法對缺失數據進行填補，得到可用數據集;其次，采用主成分分析法（PCA）進行關鍵指標選取，確定農用化肥、農作物總播種面積、農業機械總動力、農業勞動力、有效灌溉面積五個指標作為在農業GDP研究過程中的重要輸入向量。

2 結果與分析

2.1 異常數據池篩選

2.1.1 整體樣本檢驗 樣本集數據首數字的頻率分布如表3所示。可知，數據集實際頻率與Benford頻率分布趨勢基本一致，只有首數字為2時有明顯差別。因為數據集為小樣本數據，在顯著水平為0.05條件下，χ2統計量為18.056，大于自由度為8時的臨界值15.51，數據真實性較可疑。

2.1.2 時間維度檢驗 分別統計2000、2005、2010、2015年4組數據集的首數字頻率分布，結果顯示，首數字“2”的頻率與相應的Benford頻率有明顯差別（表4）;在顯著性水平0.05條件下，這4組數據的χ2統計量都小于自由度為8時的臨界值15.51，數據集質量較高（表5）。

2.1.3 空間維度檢驗 分別統計滄州、邢臺、邯鄲、保定、唐山、張家口、石家莊7組數據集的首數字頻率分布，結果顯示，數據集首數字的頻率與相應的Benford頻率有明顯差別（表6）;在顯著性水平0.05條件下，對數據集進行擬合優度檢驗，保定、張家口、石家莊的χ2統計量都大于15.51，而唐山的Pearson相關系數僅為0.931（表7），這四組數據集存在異常數據可能性較大。

綜上，滄州、邢臺、邯鄲的數據集質量較好，保定、唐山、張家口、石家莊數據質量較差，屬于異常數據池。這個異常數據池范圍較大，難以直接從中精確挖掘異常點，所以需要用SVR進一步處理。

2.2 異常數據點挖掘

通過樣本檢驗已知，滄州、邯鄲、邢臺的數據集質量較好，而保定、石家莊、唐山、張家口數據集異常可疑性較大。基于此，初步選取滄州、邯鄲、邢臺作為訓練集，共184個樣本;而唐山、保定、張家口、石家莊四個市的數據作為測試集，分別包含40、88、52、68個樣本。

2.2.1 確定訓練集 從滄州、邯鄲、邢臺的184個樣本中選取160個樣本點作為訓練集，另外24個樣本點作為預測集。用粒子群算法優化參數對（C，g），優化結果為C=1.4142，g=0.8284，帶入SVR模型中進行分析，結果（圖4）顯示，模型的MSE=0.0061，決定系數R2=0.9175，預測值和真實值差別較小，確定該樣本集可以作為訓練集。

2.2.2 異常數據挖掘 以滄州、邯鄲、邢臺的184個樣本作為訓練集，分別選擇唐山、保定、張家口、石家莊的樣本作為預測集，用粒子群算法優化參數C、g，并分別帶入SVR模型中進行訓練，再對五個地區的數據集進行異常分析。

由圖5可見，唐山數據集的MSE=0.0189，決定系數R2=0.8640，數據集誤差變大，回歸效果變差，數據集中許多樣本點的預測值和真實值存在差異，異常表現較大的10個點序號依次為189、205、157、211、195、199、185、20、213、187。

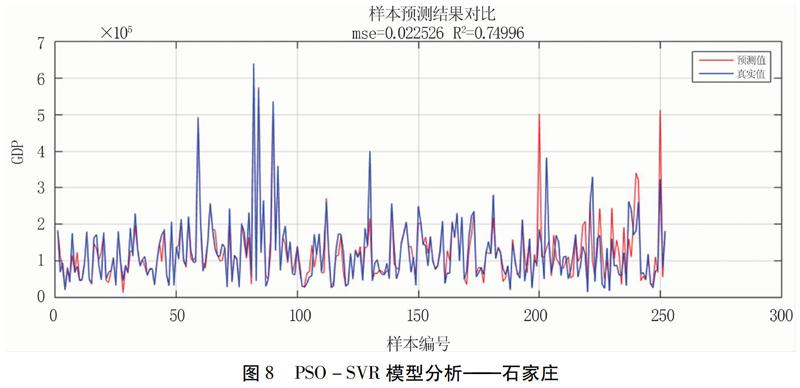
保定數據集的MSE=0.0147，決定系數R2=0.8033，異常表現最大的10個點序號依次為81、270、165、185、265、152、264、87、240、258（圖6）;張家口數據集的MSE=0.0084，決定系數R2=0.8687，異常表現最大的10個點序號依次為193、143、222、71、208、83、196、209、216、187（圖7）;石家莊數據集的MSE=0.0225，決定系數R2=0.7500，異常表現最大的10個點序號依次為226、200、19、194、202、212、227、147、236、233（圖8）。

3 討論與結論

本文在研究了Benford定律和支持向量回歸（SVR）不同特點的基礎上，充分利用兩者的技術優勢，構建了Benford-SVR異常數據檢驗的組合模型。從對河北省7個市131個縣生產數據集進行實證分析的結果看，該模型可以通過甄別數據集的數據質量，挖掘出影響數據質量的最大可疑異常點。

在當前大數據迅猛發展的背景下，數據質量的重要性更加突出，數據質量檢驗的研究也越來越受到重視。但研究不應僅停留在對數據質量的判定上，還應能有效找到“污數據”，這樣才對實踐管理工作中的數據校核、研究工作中的缺失數據插值等更具有價值[2，17]。Benford定律和SVR模型都是基于數據客觀分布規律開展分析，沒有考慮數據代表的意義或所在行業屬性[15，18]，只能在大數據背景下才有效。當前，數據檢驗模型在農業中的應用較少，雖然Benford-SVR異常數據檢驗模型已經展現出了可行性，但還需進一步研究和完善，如對異常點數據的處理以及針對行業屬性特點開展針對性的模型等。

參 考 文 獻：

[1]楊青云，趙培英，楊冬青，等. 數據質量評估方法研究[J]. 計算機工程與應用， 2004（9）：3-4，15.

[2]李國杰，程學旗. 大數據研究：未來科技及經濟社會發展的重大戰略領域——大數據的研究現狀與科學思考[J].中國科學院院刊， 2012， 27（6）：647-657.

[3]許世衛，王東杰，李哲敏. 大數據推動農業現代化應用研究[J]. 中國農業科學， 2015， 48（17）：3429-3438.

[4]黃守坤. 異常數據挖掘及在經濟欺詐發現中的應用[J]. 統計與決策， 2003（4）：32-33.

[5]王雷，張瑞青，盛偉，等. 基于支持向量機的回歸預測和異常數據檢測[J]. 中國電機工程學報， 2009， 29（8）：92-96.

[6]梁昇，肖宗水，許艷美. 基于統計的網絡流量異常檢測模型[J]. 計算機工程， 2005（24）：123-125.

[7]趙澤茂，何坤金，胡友進. 基于距離的異常數據挖掘算法及其應用[J]. 計算機應用與軟件， 2005（9）：105-107.

[8]趙春暉，王鑫鵬，閆奕名. 基于密度背景純化的高光譜異常檢測算法[J]. 哈爾濱工程大學學報， 2016， 37（12）：1722-1727.

[9]朱燕，李宏偉，樊超，等. 基于聚類的出租車異常軌跡檢測[J]. 計算機工程， 2017， 43（2）：16-20.

[10]馬黎，趙麗紅，傅惠.基于BP神經網絡的交通異常事件自動檢測算法[J].交通科技與經濟， 2010， 12（6）：47-50.

[11]Benford F.The law of anomalous numbers [J]. Proceedings of the American Philosophical Society， 1938， 78（4）：551-572.

[12]Arshadi L， Jahangir A H. Benfords law behavior of Internet traffic[J]. Journal of Network and Computer Applications， 2014， 40：194-205.

[13]de Vries P， Murk A J. Compliance of LC50 and NOEC data with Benford[KG-*3]s law： an indication of reliability [J]. Ecotoxicology and Environmental Safety， 2013， 98： 171-178.

[14]Nigrini M J. A taxpayer compliance application of Benford[KG-*3]s law[J]. The Journal of the American Taxation Association， 1996， 18： 72-91.

[15]Rauch B， Gttsche M， Brhler G， et al. Deficit versus social statistics： empirical evisence for the effectiveness of Benfords law [J]. Applied Economics Letters， 2014， 21（3）：147-151.

[16]朱文明，王昊，陳偉. 基于Benford法則的舞弊檢測方法研究[J]. 數理統計與管理， 2007（1）：41-46.

[17]劉云霞，曾五一. 關于綜合利用Benford法則與其他方法評估統計數據質量的進一步研究[J]. 統計研究，2013， 30（8）：3-9.

[18]Vapnik V N， Levin E， Cunn Y L. Measuring the VC dimension of a learning machine [J]. Neural Computation， 1994， 6（5）：851-876.

[19]項前，徐蘭，劉彬，等. 基于粗糙集與支持向量機的加工過程異常檢測[J]. 計算機集成制造系統， 2015，21（9）：2467-2474.

[20]Pinkham R S. On the distribution of first significant digits [J]. The Annals of Mathematical Statistics， 1961， 32：1223-1230.

[21]Ciornei I，Kyriakides E. A GA-API solution for the economic dispatch of generation in power system operation [J]. IEEE Transactions on Power Systems， 2012， 27（1）：233-242.

[22]丁世飛，齊丙娟，譚紅艷. 支持向量機理論與算法研究綜述[J]. 電子科技大學學報， 2011， 40（1）：2-10.

[23]杜樹新，吳鐵軍. 用于回歸估計的支持向量機方法[J]. 系統仿真學報， 2003（11）：1580-1585，1633.

[24]張麗平. 粒子群優化算法的理論及實踐[D]. 杭州：浙江大學， 2005.

[25]肖曉偉，肖迪，林錦國，等. 多目標優化問題的研究概述[J]. 計算機應用研究， 2011， 28（3）：805-808，827.