突雙基 重通法 多方位考查能力
——2019年江蘇高考數學卷有感

江蘇省溧水高級中學 (211200)

李國林

今年江蘇高考數學給人感覺是突出雙基、注重通性通法，以人為本，多方位檢測能力，學生考完之后心情平穩，整份試卷下來都有題可做，有分可拿，甚至有不少學生將第14題也算出來了，感覺沒有太大的計算量.第18，19，20題的第(3)也不在像以往年一樣，更注重學生對基礎的熟練掌握與思想方法的使用，是一份以人為本，多方位檢測能力試卷.

1.突出雙基，覆蓋面廣.

試卷覆蓋了《考試說明》中20個A級考點(總共25個)，37個B級考點(總共38個)，8個C級考點.1-9題都是基礎題，涉及集合、復數、算法、函數、統計、概率、雙曲線、數列、立幾、覆蓋面廣，與2018年江蘇數學卷題型基本相同，告訴學生思考問題不要求偏求怪，應突出通解通法；15、16題源于教材，是考生比較熟悉的基礎題，告訴學生平時的學習要做到概念清楚，基礎牢固，答題規范.

本卷既有常見的知識點交匯處設計的問題，如12題是三角和向量的綜合；也有創新型的考查學生的探究能力，如11題考查了學生的觀察、猜想、驗證，更有在思想方法上設計問題，如13題考查學生整體代換、化歸，14題考查學生數形結合.比較系統地檢測了學生的數學綜合能力.

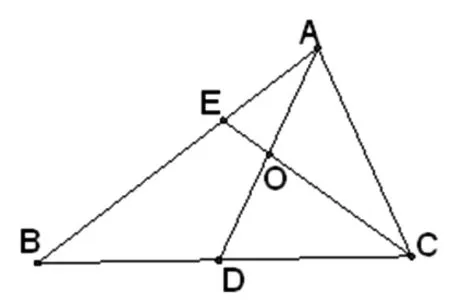
圖1

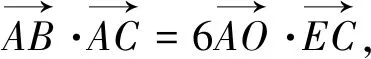
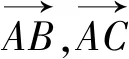
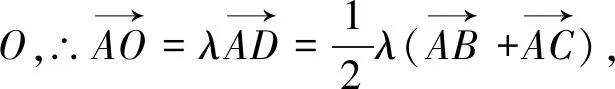
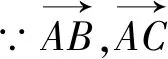
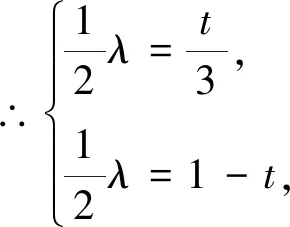
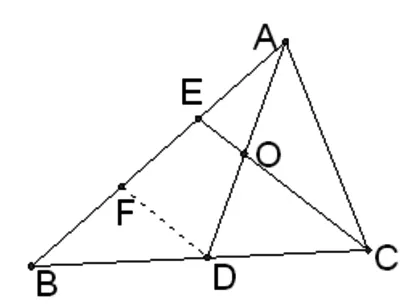
圖2

解析2：如果同學們從圖形入手，利用數形結合的思想，就會更加方便，取BE中點F，聯結DF，如圖2.

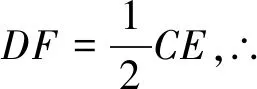
點評：本題是一個綜合題，對于學生來說，在最近的2016年第13題(2014年第12題，2013年第10題)就有考過，且難度都比今年要大一點，所以學生都知道如何下手且方法可以自由選擇.對于喜歡“坐標法”的同學，還可以考慮本題因條件較少，進而選擇“特殊化”，比如取∠ABC=90°，再建系處理.它考查了學生的基本知識、基本方法，同時也考查學生的應變能力了.

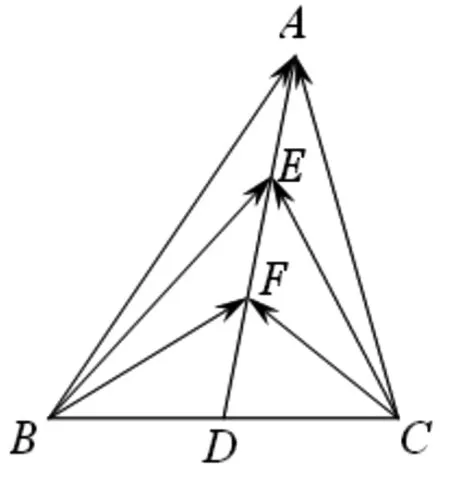
圖3

2.體現通性通法，讓學生都有題可做，有分可拿

2019年高考數學江蘇卷改變了“前面送分，后面要命”的模式，努力體現“多考一些想，少考一些算”，將思想方法盡可能融入題目中，讓想的好的學生算的少一點，想的不全面的學生算的就多一點如第19題(2)，(3)就考查學生分類討論的思想與函數最值的研究方式，第20題(2)則將“已知前n項和求通項”的表現形式作了改變，考查學生化歸的思想方法，但都不是“要命”的題，學生跳一跳還是能夠得著的.

例2 (2019江蘇卷19).設函數f(x)=(x-a)(x-b)(x-c)，f′(x)是f(x)的導函數.

(1)若a=b=c，f(4)=8，求a的值；

(2)若a≠b，b=c，且f(x)和f′(x)的零點均在集合{-3,1,3}中，求f(x)的極小值；

解析：第(2)問考查學生能不能把握分類標準或回避分類討論，但方法是通性通法，學生按部就班就能很好的處理，第(3)問考查學生在導函數零點不可求的前提下研究因變量M的最值.

解：(1)f(x)=(x-a)3，f(4)=(4-a)3=8，解得a=2.

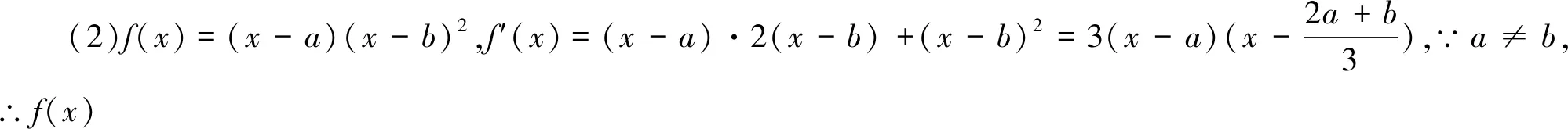
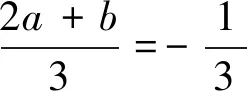
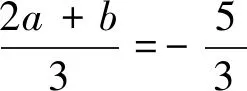
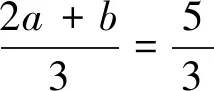
∴f(x)=(x-3)(x+3)2,f′(x)=3(x+3)(x-1).

通過列表(略)，可得f(x)在x=1處取得極小值為f(1)=-32.

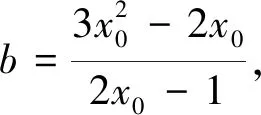
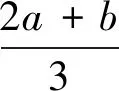
3.以人為本，多方位檢測能力

教育的根本目的就是育人，教育以培養真正的人，培養全面、完整的人為己任.德國教育家赫爾巴特指出：教育具體落實在教師職業行為上就是通過叫教師勞動培養人、塑造人、改造人、促進人的全面發展.同時高考又影響教師教育的一項重要因素，高考也是教師的“指揮棒”，所以要想教師改變教學方法，那么高考試卷就應該有所體現.

一份試卷有沒有“以人為本”，關鍵是學生是否愿意去做，是否喜歡去做，因為不管“好生”、“差生”，應該都有他們能解決的問題.這樣才能讓學生不討厭“數學”，嘗試用“數學”去解決問題，更要由此為導向，提醒教師在教學中要注重“以人為本”，提升學生的潛能，才能讓學生通過多方位檢測.

例3 (2019江蘇18題)如圖4，一個湖的邊界是圓心為O的圓，湖的一側有一條直線型公路l，湖上有橋AB(AB是圓O的直徑)．規劃在公路l上選兩個點P、Q，并修建兩段直線型道路PB、QA．規劃要求：線段PB、QA上的所有點到點O的距離均不小于圓O的半徑．已知點A、B到直線l的距離分別為AC和BD(C、D為垂足)，測得AB=10，AC=6，BD=12(單位：百米)．

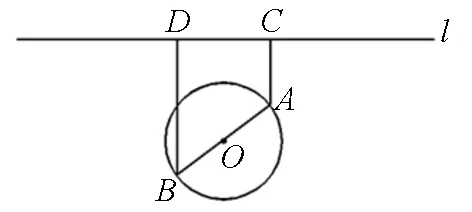
圖4

(1)若道路PB與橋AB垂直，求道路PB的長；

(2)在規劃要求下，P和Q中能否有一個點選在D處？并說明理由；

(3)在規劃要求下，若道路PB和QA的長度均為d(單位：百米).求當d最小時，P、Q兩點間的距離．

解析：本題考查學生處理實際問題的能力，涉及解直角三角形、余弦定理、直線與圓位置關系、分類討論，特別是圖形較復雜，學生比較陌生，但問題的設計層層推進，給學生搭了臺階，讓學生能比較輕松的解決(1)(2)兩問，第(3)問讓學生解決實際問題(且沒有自變量)，難度教大，讓不同的考生有不同的發揮余地.

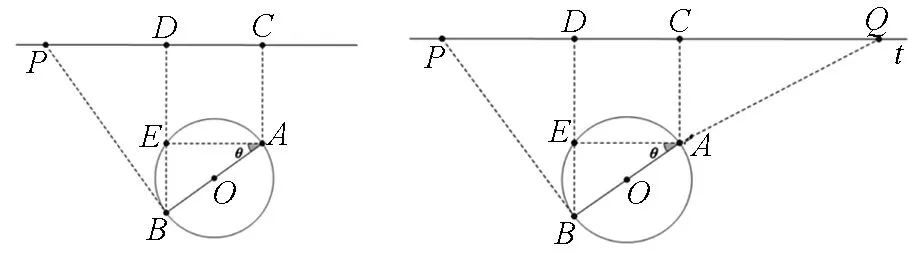
圖5 圖6

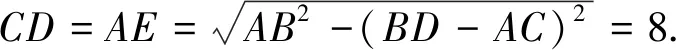
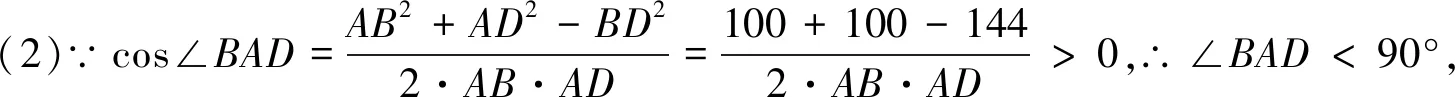
(3)先討論點P的位置.

當∠OBP<90°時，線段PB上存在點到點O的距離小于圓O的半徑，點P不符合規劃要求；

當∠OBP≥90°時，對線段PB上任意一點F，OF≥OB，即線段PB上所有點到點O的距離均不小于圓O的半徑，點P符合規劃要求.

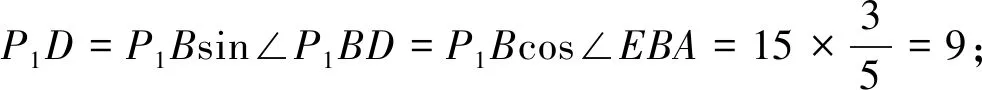
當∠OBP>90°時，在△PP1B中，PB>P1B=15.由上可知，d≥15.

再討論點Q的位置.

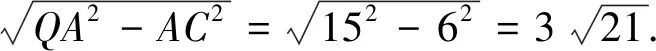
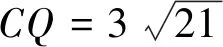
點評：本題背景清晰、創新性高，學生一開始突然碰到較復雜的圖形，可能會比較陌生，但問題設置層次鮮明，第(1)問是讓學生能理解題意，第(2)問是讓學生能解決簡單的幾何問題，學生若都能認真分析、思考，跳一跳就能多得一點分數，但有些學生做第(3)問時方法停在如何構造距離d的函數，就會調入思維陷阱,本題也可建系，利用直線與圓的位置關系來解題.

4.結束語

愛因斯坦曾今說過：教育應該使提供的東西，讓學生作為一種富貴的禮物來享受，而不是作為一種艱苦的任務要他負擔.經常聽到有學生說討厭數學，不喜歡做數學題，這與我們的基礎教育是不符的，這份試卷讓學生都能去做，都能得分，都能將自己所學發揮出來，學生進考場是帶著“害怕”的，出考場是“愉悅”的，讓“好生”感覺自己能多得分，讓“差生”感覺自己得到不少分，才是一份成功的試卷.因為它轉變了考生學習數學的狀態.同時它也指導我們教師在傳授知識中要重視“四基”、“四能”，注重提升學生的數學素養；不能盲目的刷題，讓學生害怕數學.