九年級數學問題串式教學模式的實踐與思考

陶霞

[摘 ?要：九年級學生即將面臨升學考試，學習任務重、壓力大，經常會感到身心俱疲。數學是一門學習難度較大的學科，但并不是一門光靠死記硬背就能學好的學科，學生所付出的時間與努力并不一定會得到同等的回報，因此，數學教師應從學生的角度出發，采用問題串式模式進行教學，在激發學生興趣的基礎上不斷提高其學習效果。

關鍵詞：九年級數學;問題串式教學模式;數學教師]

一、前言

數學是一門對理性思維能力要求較高的學科，對學生的思維能力與思考能力有著較高的要求，但由于課堂教學時間有限，想要充分提高課堂教學的作用與價值，教師必須要對傳統的教學模式進行改革，讓學生能主動參與到課堂教學當中，積極進行思考、探究。問題串教學模式主要是利用問題來激發學生興趣，讓其能多層次、多角度進行思考與學習，在不斷的探究中獲得知識、獲得進步，從而促進課堂學習效果的提高。因此，初中數學教師可以利用問題串教學模式進行教學，幫助學生將數學知識點串聯起來，形成條理清晰的數學架構，從而使得學生學習與復習變得更加得心應手。

二、設計生活化問題串，激發學習興趣

數學也是一門源于生活的學科，教師在教學的過程中不能脫離生活而教學，而應當通過生活化的問題串來引導學生進行學習與探究，從而消除學生對數學的恐懼感與陌生感，并提高其學習興趣與效果。例如教師在教學的過程中可以根據廈門等沿海地區臺風情況一系列的問題串，以供學生進行探究，具體如下：

題目：廈門氣象臺監測發現近日將有臺風抵達，臺風中心現在在廈門市正西400km的地方，移動速度為107km/h，移動方向為由北偏東45°，以臺風中心為中心點向外擴散200km地方為受影響區域。

問題1：廈門市是否在本次臺風的影響范圍內？你的理由是什么？

問題2：如若廈門市屬于本次臺風影響范圍，那么影響的時間會持續多久？

問題3：如果廈門某港口有一艘輪船正在進行緊急卸貨，為了避免貨物損失，他們需要在多長時間內卸完貨？

問題串教學模式的主要特點在于一個問題可以設計到許多不同的知識點，學生需要將所學的知識串聯起來去解決問題，而不只是簡單盯著某一章某一節，這對于其數學思維能力的提高具有重要的作用。同時，為了充分發揮問題串教學模式的作用與效果，教師也可以將課后作業設計為問題串模式，以檢驗學生的知識運用情況，了解其學習的盲區，從而使得教學更具有針對性。

三、設計變式性問題串，培養數學素養

數學題目雖然千變萬化，但“萬變不離其宗”，這是中學數學的規律與特點，學生在做題的過程中之所以不知道如何下手，主要是因為學習不夠深入，難以盡快找到破題的關鍵。因此，教師在教學的過程中應加強變式訓練，使得學生在復習的過程中可以拓寬復習的知識與內容，從而不斷提高思維能力、解題能力以及綜合運用能力。如教師在指導學生復習《圓》這個章節的內容時，可以將以往的知識點與圓中常見直角三角形構建結合起來形成變式性的問題串，具體如下：

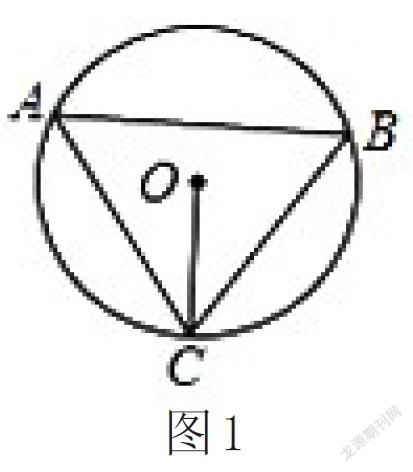
題目：如圖1☉O為△ABC的外接圓，現在已經知道∠ACO的度數為30°。

問題：①∠B的度數為多少？②如若sinB=3/5，OC=10cm，那么AC的長為多少？

以上幾個問題均是根據一道簡單題目所設計的問題串，教師可以根據自身的教學習慣與教學重點來豐富問題的設計，讓學生在一道題目中接觸到完全不同章節的知識點，并逐步掌握思考問題的方式方法，懂得聯系以往學習過的知識來解決問題，使得自身的數學素養得到不斷提高。當然，對于學生尚未完全掌握的知識點，教師必須要及時進行查漏補缺，幫助其盡快夯實知識基礎，讓學生逐步懂得靈活運用不同的知識點來解決相同的問題，在解決問題的過程中能做到舉一反三。

四、設計開放式問題串，鍛煉數學思維

數學是一門十分講究嚴謹與邏輯的課程，在學習數學的過程中，學生則深刻體會到什么叫做“失之毫厘，差之千里。”因此，教師應當注重鍛煉學生開放、嚴謹的數學思維，讓其學會從不同的角度去思考問題，而不是一味地按部就班、墨守成規。例如學習到特殊平行四邊形性質時，教師可以設計一些開放性問題串來鍛煉學生的數學思維，題目如下：

題目：如圖2在△ABC中，AB=AC，AD為∠BAC外角平分線，AE為∠BAC外角平分線，且CE⊥AE于點E。

問題：①AB與DE的長度是否相等？為什么？②如何證明四邊形ABDE是一個平行四邊形？

最近幾年來，數學考卷中的題目越來越具有創新性與新穎性，重點考察學生的開放性思維能力，教師應當將思維鍛煉納入教學目標，不斷提高學生思維的嚴謹性，讓其在解決問題時每一步都應做到環環相扣。在這個過程中，教師還應當給予學生更多鍛煉的機會，讓其學會用不同的方法去解決同一個問題，使得問題的解決能實現殊途同歸，以此不斷提高學生的思維能力。

五、結語

總而言之，數學的學習并沒有想象中的簡單，關鍵是要掌握思維與方法。九年級學生已經臨近畢業，學習時間非常緊張，教師想要讓學生在如此緊張的學習過程中獲得較高的學習效率，則應采用問題串教學模式進行教學，讓學生能靈活運用教材中的知識點去分析問題、解決問題，掌握相關的解題思路與解題方法，從而不斷提高自身的數學思維能力與學習效果。

參考文獻

[1]陸麗萍.基于協同學理論的情境問題串數學課堂教學模式行動研究[J].數理化解題研究，2016（26）：31.

[2]丁燕.初中數學“問題串”教學的現狀探討[J].江西教育，2016（24）：21-22.

[3]孫彪.以“問題串”貫穿課堂教學——談問題式教學法在初中數學課堂的運用[J].中學教學參考，2014（08）：19.

[4]姜曉翔.問題成串導思維，生本課堂促高效——例談初中數學問題串導學策略的實踐與應用[J].中學數學，2015（02）：52-55.