促進數學深度學習的教學策略舉隅

張蕾萍

摘要：針對初中數學教學中出現的被動、孤立、機械的淺層學習而提出的數學深度學習，不僅強調積極主動的學習狀態、知識整合和意義聯結的學習內容、舉一反三的學習方法，還強調高階思維的發展和復雜問題解決能力的提升。促進數學深度學習的教學策略有：情境創設，應注重激發學生的認知需求;問題設計，應注重發展學生的高階思維;意義建構，應注重知識的聯系整合;能力提升，應注重過程的反思總結。

關鍵詞：初中數學?深度學習?認知需求?高階思維

黎加厚教授認為，深度學習是在理解的基礎上，批判地學習新思想和事實，并將它們融入原有的認知結構中，在眾多思想和事實間進行聯系，并將已有思維、知識遷移到新的情境中，做出決策和解決問題的學習。針對初中數學教學中出現的被動、孤立、機械的淺層學習而提出的數學深度學習，不僅強調積極主動的學習狀態、知識整合和意義聯結的學習內容、舉一反三的學習方法，還強調高階思維的發展和復雜問題解決能力的提升。

促進數學深度學習的教學，要超越知識的表層符號，深入研究知識的發生、發展過程，創設激發學生認知需求的情境，設置有挑戰性的問題，引導學生通過自主探究建構知識，促進學生將新舊知識相融合，將眾多思想相關聯，并有效地遷移知識、解決問題，進而實現由知識建構向能力提升的轉變。

一、情境創設，應注重激發學生的認知需求

深度學習是基于已有的知識和經驗，通過同化或順應來建構新知識的過程。創設適當的情境可以喚醒學生的已有知識和經驗，促使新舊知識發生沖突，引發問題，維持、強化、調整學生的學習興趣，激發學生的認知需求，從而開啟深度學習之旅。

（一）從數學外部問題出發創設情境

數學知識往往較為抽象，甚至枯燥，無法有效吸引學生的注意。因此，教學過程中，教師應注重依據素養培養目標、教學內容和學生的認知特點等，設置如生活實際、實物演示、圖畫再現、史料故事等生動直觀、易于理解的數學情境，激發學生的學習動力。

例如，教學“同類項”時，將書本、粉筆、卡片、三角板等散落在講臺上，請學生整理，學生很容易用分類的方法整理好。同時，展示超市琳瑯滿目、錯落有致的商品陳列畫面，讓學生感受到分類廣泛地存在于生活中，并體會到分類的必要性。

再如，教學“軸對稱圖形”時，呈現一組圖片并引導學生觀察思考：根據圖1中一半的圖形，猜猜畫的是什么？你們覺得圖2中的圖形美不美，它們有什么共同點？可以從哪兒將這些圖形分為左邊和右邊？怎么才能知道這些圖形左邊和右邊完全相同？這些從數學外部過渡到數學內部的問題情境，讓學生從想象到體驗、從學習到運用逐層深入，喚起學生強烈的求知欲望。

（二）從數學內部問題出發創設情境

從數學內部問題出發，在知識的易錯點、交匯點處設置懸念，引發學生原有認知結構與新的學習內容之間的沖突，可以激發學生積極思考，引發學生主動探究，幫助學生迅速進入學習狀態。

例如，教學“正弦、余弦”時，設計情境：（1）直角△ABC中，∠C=90°，已知斜邊AB和一條直角邊AC，如何求另一條直角邊BC？（2）直角△ABC中，∠C=90°，已知∠A和斜邊AB，如何求∠A的對邊BC？對于情境（1），學生自然會想到勾股定理。而對于情境（2），學生會發現利用勾股定理無法解決，從而產生認知沖突，進而產生迫切的求知欲。

再如，教學“乘法公式”時，很多教師通過利用兩種方法計算圖形面積引入乘法公式，但是學生會生發“怎么知道計算這個圖形的面積就能得到乘法公式”的疑問。學生做得到，但是想不到，就是“假探究”，不是深度學習。其實，多項式乘法是乘法公式的知識生長點：在多項式乘法（a+b）（c+d）=ac+ad+bc+bd中，若字母a、b、c、d有某些特殊關系，就有相應的乘法公式，如a=c、b=-d時有平方差公式，a=c、b=d時有完全平方公式。因此，乘法公式是多項式乘法的特例。“考察特例”是數學研究的基本“套路”，體現了從一般到特殊、歸納的思想。據此，教學“乘法公式”時，可引導學生先復習多項式乘法運算，再探究多項式乘法法則有哪些特殊情形，能夠得到哪些特殊結論。這樣的設計，切合知識發生、發展的過程和內在的邏輯線索，符合學生的認知規律;學生自主尋找特例，探究的空間大，是“真探究”，是深度學習。

二、問題設計，應注重發展學生的高階思維

數學教學是思維活動的教學，而問題是思維的起點與動力。將教學的內容與能力要求設計成具有系統性和靈活性、環環相扣且層層推進的問題，能引導學生的思維由淺入深、由表及里，有效發展學生的高階思維。

（一）設計遞進性“問題串”

深度學習不是一蹴而就的，需要逐步深入。教學中，教師要從學生的“最近發展區”出發，設計由簡到繁，由易到難，由具體、明確、封閉和單一到抽象、模糊、開放和綜合的遞進性“問題串”，促使學生不斷深入思考，思維水平也由感知、記憶等較低層次向抽象與概括、判斷與推理等較高層次不斷提升。這樣的“問題串”在知識教學和習題教學中有廣泛的應用。

例如，教學“圓周角定理”時，設計如下“問題串”，引領學生經歷類比、作圖、觀察、猜想、度量、驗證、分析、論證、轉化、歸納等活動，由感性到理性、由特殊到一般地探究圓周角定理，理解知識的發生、發展過程，感悟相應的數學思想方法，提升思維的深刻性。

問題1類比圓心角的結論（同弧或等弧所對的圓心角相等），同弧或等弧所對的圓周角相等嗎？

問題2先畫一個圓心角，再畫同弧所對的圓周角，你能畫多少個？所畫的圓周角（的度數）與圓心角（的度數）有何關系？先猜一猜，再用量角器量一量，你有何發現？

問題3一條弧所對的圓心角只有一個，而圓周角有無數個，如何用你所學的知識來推理論證它們之間的關系呢？

問題4在你所畫的圖中，圓心與圓周角的位置關系有幾種情況？

問題5當圓心在圓周角的一邊上時，如何證明？

問題6其他的兩種情況下，如何證明？可否轉化為上述情況？

再如，教學“相似三角形的性質”時，設計如下“問題串”，從特殊到一般，不斷放寬條件，引導學生在不同的情境中逐步遷移運用“相似三角形對應線段（高）之比等于相似比”這一性質及已有經驗解決問題，促使思維不斷走向深刻。

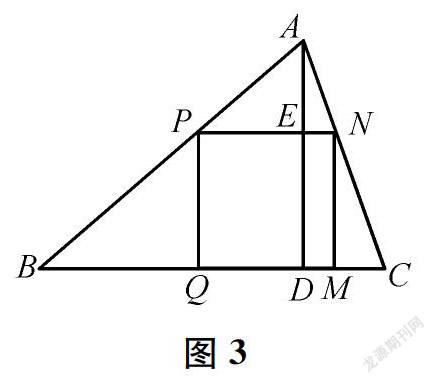
如圖3，有一塊三角形余料ABC，邊BC=120 cm，高AD=80 cm。要把它加工成正方形零件PQMN，使正方形的一邊QM在BC上，其余兩個頂點P、N分別在AB、AC上。

問題1加工成的正方形零件的邊長是多少？

問題2如果原題中所要加工的零件是一個矩形，且長寬之比為2∶1，那么怎么加工，此矩形的面積最大？

問題3如果原題中所要加工的零件是一個矩形，那么此矩形的面積最大是多少？

（二）設計辨析性問題組

深度學習強調批判地學習新思想和事物。教學中，教師可從學生學習的易混點出發，設計既有聯系又有區別、形似神非的辨析性問題組，促使學生自覺反思并發現學習過程和已有認識中的不足與錯誤，進行質疑、批判、完善和修正。

例如，教學“分式方程”時，學生遇到含待定系數的分式方程“無解”“有增根”等問題時，常常把它們混為一談;遇到含待定系數的分式方程“有特殊解”的問題時，常常忽視增根。因此，設計如下問題組，引導學生在比較中辨析，在反思中完善和修正，發展思維的批判性。

分式方程需要去分母轉化為整式方程求解。分式方程有增根即轉化后的整式方程有解，但不是原分式方程的解，即原分式方程分母為0。分式方程無解包括兩種情況：一是轉化后的整式方程無解，二是轉化后的方程有解，但相應的解是原分式方程的增根。即有增根是無解的一種情況。

題組1的三道題引導學生辨析“無解中的有增根”“無解中的有增根和無增根”和“無解即有增根”三種情況。題組2的兩道題引導學生辨析“特殊解中包含增根”和“特殊解中不包含增根”兩種情況。

三、意義建構，應注重知識的聯系整合

數學知識之間是存在內在聯系的。加強知識之間的聯系與整合，有助于充分理解知識，靈活遷移運用，是深度學習的體現。教學中，教師需要引導學生發現所學知識之間的聯系，從而對知識進行整合，使之條理化、系統化，促進學生進行有意義的知識建構。

（一）建立知識聯系

數學各部分知識在內容上、方法上是相互滲透、縱橫關聯的。教學中，教師既要注意知識間的橫向聯系，又要注意知識間的縱向聯系，從而設計好相應的“先行組織者”，引導學生進行有意義的學習，不斷擴充和豐富已有的知識和經驗，做到舉一反三、觸類旁通。

例如，教學“矩形、菱形、正方形”時，提出以下問題：學習平行四邊形時，你積累了哪些研究經驗和策略？你覺得可從哪些角度來研究矩形、菱形、正方形？引導學生類比遷移研究平行四邊形的方法，從邊、角、對角線等角度來探究矩形、菱形、正方形的特殊性質。

再如，教學“二次函數”時，提出以下問題：（1）一般從哪些方面研究函數？（2）根據研究一次函數圖像與性質的經驗和策略，你覺得應如何研究二次函數的圖像與性質？第一個問題引導學生根據一次函數、反比例函數的學習經驗概括函數研究的一般思路，即從函數的概念、圖像、性質以及應用等方面來研究，讓學生知道“學什么”。第二個問題引導學生類比研究一次函數從y=kx到y=kx+b、從k>0到k<0的思路來研究二次函數，即從y=ax2到y=ax2+k、y=a（x+h）2 再到y=a（x+h）2+k、y=ax2+bx+c，從a>0到a<0，研究圖像的形狀、位置、增減性以及位置關系等。

（二）發展認知結構

教學中，教師還要注意引導學生把不同的知識片段和模塊聯結起來，整合成有序的認知組塊，發展出完整的認知結構。

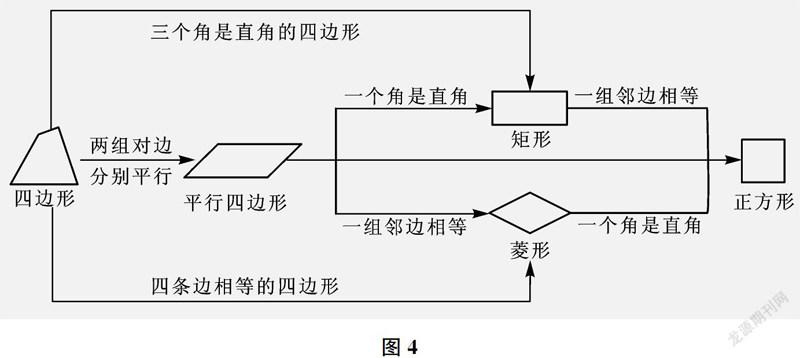
例如，教學完《中心對稱圖形——平行四邊形》一章后，教師可以指導學生小組合作繪制思維導圖（如下頁圖4），將相關知識結構化組織、模塊化架構和網絡化呈現，發展學生的認知結構。

四、能力提升，應注重過程的反思總結

學習反思是對學習活動進行審視、分析、評價、調節的過程，有助于學習的真正深入以及對內容的本質理解，發展元認知，提升學習能力。教學中，教師要及時引導學生反思總結自己的學習過程。

一方面，知識教學中，教師要引導學生反思知識探究的過程，提煉獲取數學知識的思想方法和有效策略，提高獲取知識的能力。如，教學“圓周角定理”時，探究得出“圓周角的度數等于它所對弧上的圓心角度數的一半”后，教師要引導學生反思獲得這一結論的探究過程，提煉相應的數學思想方法：猜想結論時，將直觀操作和邏輯推理有機結合;論證結論時，先通過畫圖探究圓心與圓周角的關系有幾種情況，體現了分類思想，再通過添加輔助線將“圓心在圓周角內部”“圓心在圓周角外部”這兩種情況轉化成“圓心在圓周角邊上”的情況，體現了化未知為已知、化復雜為簡單、化一般為特殊的化歸思想。

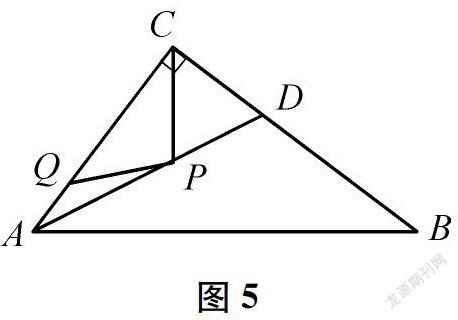
另一方面，習題教學中，教師也要引導學生反思問題解決的過程，提煉問題的類型、特征以及解決問題的思想方法和有效策略，并思考問題的推廣與變式以及解法的普適和優化，提升解決問題的能力。如，解決問題“如圖5，在△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分線。若P、Q分別是AD、AC上的動點，則PC+PQ的最小值是”后，教師要引導學生反思解題過程：這是“已知兩個動點P、Q（分別在兩條直線上）和一個定點C，求有關的兩條線段長PC、PQ的和的最小值”的問題，只要將一個動點Q看成定點，就可以轉化為比較熟悉的“兩定點（直線外）、一動點（直線上），求距離和的最小值”的問題，即將軍飲馬問題，就可以通過找對稱點實現“折轉直”，再利用“垂線段最短”來解決。由此，讓學生充分體會化陌生為熟悉的轉化思想。

參考文獻：

[1] 王寶斌.基于“問題鏈”，發展高階思維——以化學教學為例[J].教育研究與評論（中學教育教學），2016（12）.

[2] 王弟成.引導探究，強調思想——對《橢圓的幾何性質》一課的點評[J].教育研究與評論（中學教育教學），2017（12）.

[3] 〔美〕D.P.奧蘇伯爾，等.教育心理學——認知觀點[M].佘星南，宋鈞，譯.北京：人民教育出版社，1994.