微課程教學的設計與實踐*
——以“中心極限定理”為例

汪麗娜 龐晶 （內蒙古工業大學理學院）

微課程是微型學習的一種具體形式，主要以短時視頻為載體記錄微型化的教學內容，是對傳統教學模式的革新[1]。為貫徹落實《教育部關于全面提高高等教育質量的若干意見》精神，推動信息技術與大學數學課程教學深度融合，促進教師更新教學理念、革新教學方法、創新教學設計、提升教學能力，由教育部高等學校大學數學課程教學指導委員會和全國高等學校教學研究中心共同主辦了“全國高校數學微課程教學設計競賽”，促進了數學類課程教育教學改革的發展、積累了教學成果。

微課程具有短小精悍可重現的教學優勢。與傳統教學50分鐘一節課的安排方式相比，微課程的教學時間較短，更利于集中注意力學習，符合認知規律。其次，微課程是對某個具體的知識點展開教學，與傳統教學相比，其主題更加突出、針對性較強。此外，微課程視頻易于保存傳播，具有更高的教學可重現性，可以供多位教師多次再利用，也可以供學生預習復習使用。本文以概率論與數理統計中最重要的一類定理——中心極限定理為例，闡述微課程教學設計及其實踐。文章第一部分介紹中心極限定理的教學特征；第二部分給出中心極限定理的微課程教學設計；第三部分闡述微課程實踐的特點。

一 中心極限定理的教學特征

在概率論當中，將“相互獨立的隨機變量和的極限分布為正態分布”這樣的定理統稱為中心極限定理。它是概率論當中最重要的一類定理，具有廣泛的實際應用背景。例如，應用中心極限定理規劃雨量站網設計[2]，使得降水監測更科學、經濟；應用中心極限定理計算股價期權價格[3]；中心極限定理在保險精算[4]等行業中的應用。

多數本科非數學專業概率論與數理統計教材中，中心極限定理包括：列維——林德伯格定理和棣莫弗——拉普拉斯定理。2019年考研數學大綱中對中心極限定理的考試要求是：了解列維——林德伯格定理和棣莫弗——拉普拉斯定理（數學一）；了解列維——林德伯格定理、棣莫弗——拉普拉斯定理，并會用相關定理近似計算有關隨機事件的概率（數學三）。

中心極限定理的教學安排在隨機變量、分布函數、數字特征等先修內容之后，抽樣、估計、檢驗等統計學教學內容之前。從這個意義上講，中心極限定理可以看作是概率、數理統計兩部分的銜接，有著承上啟下的作用。一方面，中心極限定理可以刻畫正態分布的形成機制，解釋正態分布的普遍性；另一方面，中心極限定理是大樣本統計推斷的理論基石，是學習后續知識的基礎。從教學地位、教學目標、教學內容三個方面，中心極限定理都占有重要的位置。與之形成鮮明的對比，在課程考核時，中心極限定理被忽略了。近10年的碩士研究生入學考試中，沒有涉及到中心極限定理的考題。

雖然中心極限定理應用廣泛、地位重要，但是考試“指揮棒”沒有指到這個知識點，造成很多學生學習中心極限定理不夠積極，部分教師對中心極限定理的教學不夠重視。現有中心極限定理教學中存在一些問題：教學內容缺乏巧妙的設計；教學手段比較簡單，形象化演示不足；教學中的應用場景做得不夠好，缺乏案例設計。

二 微課程教學設計

中心極限定理從理論上說明了“許多類型”的隨機變量，它們的極限分布服從正態分布，這既肯定了正態分布在概率論中的重要地位，也為計算概率提供了強有力的手段。考慮到授課對象是理工科非數學專業本科生，他們的主要專業需求和未來職業需求是應用概率統計的思想和方法。因此，教學設計中，重點強調中心極限定理的研究對象和應用中心極限定理解決實際問題。選取案例時，選擇學生易于產生共鳴的題材；證明定理時，注重形象化的展示；應用定理時，清晰明了地強調如何使用。

列維——林德伯格定理微課程的教學設計以如何設置住宅小區的停車位數量開篇，引出中心極限定理的研究對象：獨立隨機變量的和。使用數值模擬方式，形象化地展示案例，啟發學生提出猜想，引出列維——林德伯格定理。省略定理的證明，采用數值模擬的方法形象化地驗證定理內容。最后，使用列維——林德伯格定理計算開篇提出的案例：小區停車位數量問題。

隨著私家車保有量的增加，住宅小區停車問題越來越嚴重。根據小區的地理位置、預期房價、未來業主情況等信息，獲知某住宅小區一千戶居民的戶擁有汽車數量的分布情況，問如何設置該小區的停車位數量，使得每輛車具有一個車位的概率不小于0.97。以此案例開篇，引導學生：已知戶擁有汽車量的分布，如果能夠得到一千戶居民擁有汽車量的分布情況，問題可解。由此引出中心極限定理的研究對象：隨機變量和的分布。此外，采用數值模擬的方法將一千戶居民擁有汽車數量的分布情況呈現，引導學生大膽猜想：和隨機變量服從什么分布。

棣莫弗——拉普拉斯定理微課程的教學設計以二項分布在醫學、保險精算、質量檢測等方面的廣泛應用開篇，提出問題：在分析計算實際問題時，不可避免地涉及二項概率的計算，n 較大時直接用公式計算比較煩瑣，有更方便的計算方法嗎？開門見山地引出棣莫弗——拉普拉斯定理：n 充分大時，二項隨機變量漸近服從正態分布。從數學證明、數值模擬兩個方面驗證定理內容。然后，利用定理解決開篇提出的實際問題：保險盈利的概率。

三 微課程教學實踐

1 案例教學

案例一：設置合適的停車位數量。隨著私家車保有量的增加，停車問題越來越嚴峻。根據地理位置、預期房價、目標業主情況等信息，獲知某住宅小區居民每戶擁有汽車數量X 的分布律為：P(X=0)=0.3，P(X=1)=0.6，Ps(X=2)=0.1；問：小區共有1000 戶住戶，需要多少停車位，可以使該每輛車擁有一個車位的概率不小于0.97。

案例二：隨機誤差服從正態分布。以加工零件為例，一位工人在機床上加工零件，加工過程中受到一些隨機因素的影響：噪聲干擾、電磁場微變；空氣擾動、大地微震；機床本身有磨損；工人的技術熟練程度不同；工人感覺器官無規律變化等等。這些隨機因素的影響使得加工出的零件與要求存在一定誤差。這個隨機誤差是由大量的微小的相互獨立的隨機因素綜合影響構成的，因此，根據中心極限定理它近似服從正態分布。

案例三：戀愛保險盈利的概率。2017年初，某網絡平臺推出一項戀愛保險：投保人支付少量的保金（有三個檔次），如果在第3～13年內結婚，可以獲贈近保金20 倍的祝福金。這項保險具有祝福和承諾的美好含義，推出當天即售出1.5 萬份。簡化實際問題，假設每個投保人交納99 元保金，符合約定條款的概率為0.04，符合約定條款后可獲贈祝福金1999 元。忽略其他成本，如果有一萬人投保，問：保險公司獲利的概率是多少？

將案例引入教學中，學生可以認識到抽象的定理在現實中的應用，啟發學生數理統計的廣泛應用，提高學生的學習興趣，引導他們喜愛數理統計。在中心極限定理微課程教學實踐時，使用了三個案例。這些案例來源于實際，貼近學生生活，使教學更生動；此外，理解這些案例不需要深厚的專業知識，適用于各個學院的學生，應用范圍較廣。引入列維——林德伯格定理時，使用數值模擬方法處理了案例一，合理設置住宅小區的停車位數量；講授列維——林德伯格定理的應用時，使用了案例二，解釋為什么物理實驗中將隨機誤差認定為服從正態分布；在應用棣莫弗——拉普拉斯定理處理實際問題時，使用了案例三，啟發學生初步了解保險精算。

2 形象化教學

形象化教學可以將抽象的內容具化地展示出來。在棣莫弗——拉普拉斯定理的微課程教學設計中，采用數學證明和數值模擬相結合的方式驗證定理內容。如圖1 所示，每次生成一萬組隨機數、每組一百個數據。圖1 是參數為n=100，p=0.2 的二項分布隨機數頻率直方圖。圖形呈現出“中間高、兩邊低、左右對稱”的特點，符合正態鐘形曲線的特征。圖1 的數值模擬柱狀圖不僅輔助了定理的證明，而且鍛煉了學生發現問題的能力，引導他們先大膽猜想再嚴格證明，這也是科學研究中常用的一種思維方式，理論證明與數值模擬相符。

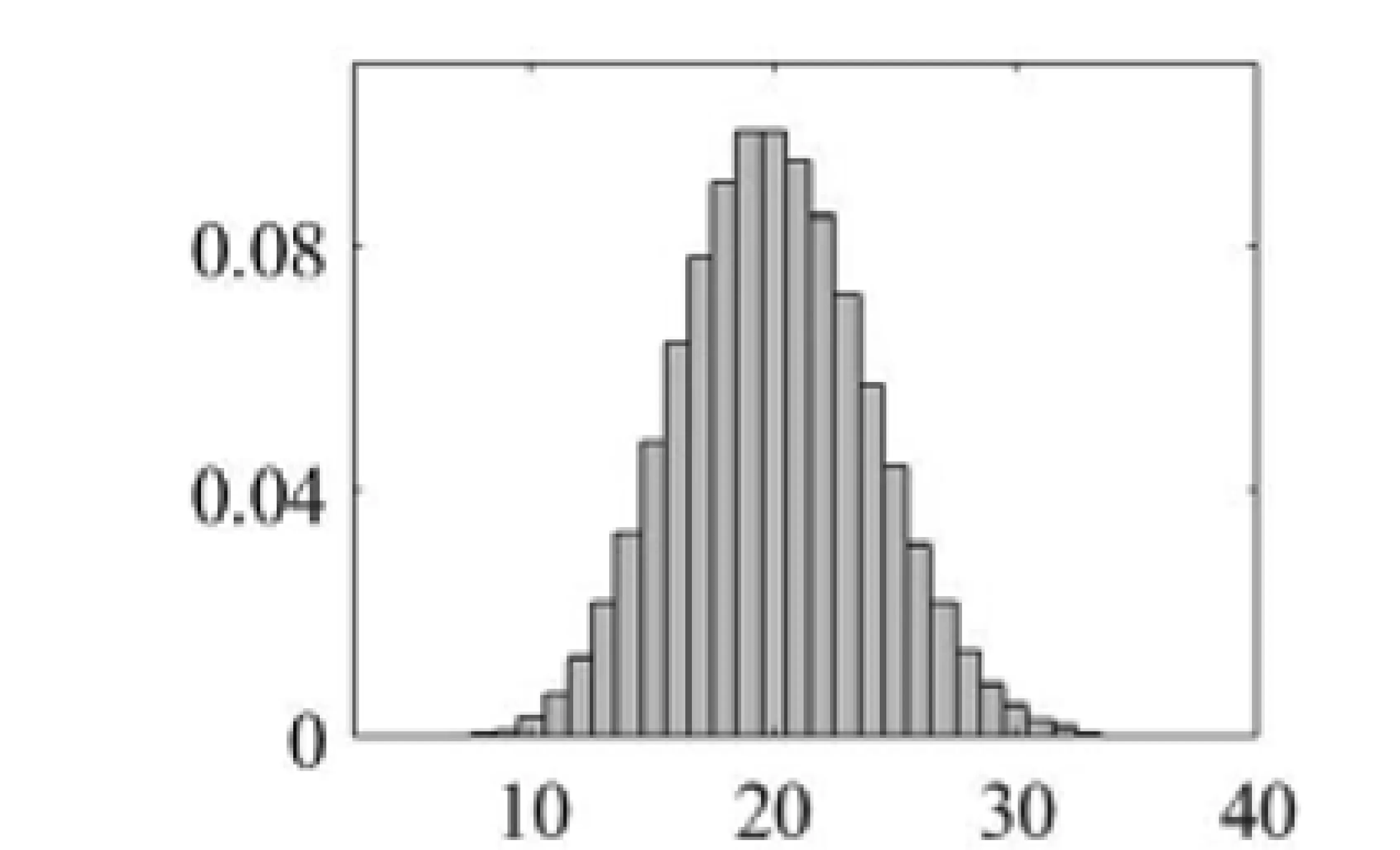
圖1 二項分布隨機數頻率直方圖

此外，某些情況下受知識所限不能給出嚴格證明時，形象化教學可以起到驗證證明的輔助作用。由于知識所限，教材中省略了列維——林德伯格定理的證明。在微課程教學實踐中，我們使用數值模擬方法驗證了定理的內容，形象化地展示了列維——林德伯格定理，這有利于學生理解和領悟定理內容，如圖2 和圖3 所示。圖2 以指數分布為例，數值模擬了列維——林德伯格定理。生成參數為二分之一的指數分布隨機數，每次生成一萬組、每組 n 個數據（a：n=1；b：n=2；c：n=10；d：n=100），計算隨機數的和，做頻率直方圖。觀察這些直方圖，隨著n 的增加，圖形呈現出鐘形曲線的特征，趨近正態曲線。通過圖2 的演示，學生可以觀察到：隨著隨機變量疊加之個數的增大，曲線由偏態逐漸向正態接近的動態演化過程，加深學生對中心極限定理的理解。

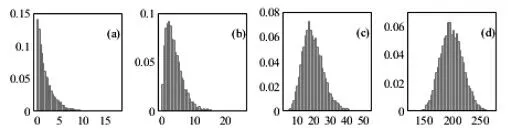
圖2 以指數分布為例，展示列維—林德伯格定理

圖3 以一些常見分布為例，數值模擬列維——林德伯格定理。分別生成四種不同分布（圖3a：參數為2 的泊松分布；圖3b：參數為0、4 的均勻分布；圖3c：參數為三分之一的幾何分布；圖3d：參數為10、0.2 的二項分布）的隨機數，每次生成一萬組、每組100 個數據；計算隨機數的和，做頻率直方圖，可以觀察到圖形呈現出正態鐘形曲線的特征。圖3 的可視化展示再次印證了中心極限定理的重要作用：不論隨機變量服從什么分布，不論隨機變量是離散型還是連續型，滿足一定條件時，隨著隨機變量個數的疊加，部分和隨機變量都近似服從正態分布。

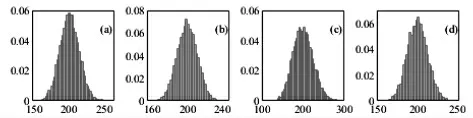
圖3 以一些常見分布為例，展示列維—林德伯格定理

3 教學的系統性

教學設計中融入簡短的科學發展史信息，提高學生對中心極限定理的認知。在概率論與數理統計教材和教學中，遵循了從一般到特殊的邏輯規律，將列維——林德伯格定理安排在棣莫弗——拉普拉斯定理的前面；并且，使用列維——林德伯格定理的一般性結論證明了棣莫弗——拉普拉斯定理。事實上，從歷史發展進程的角度，棣莫弗——拉普拉斯定理出現的更早。1733年，棣莫弗研究了二項概率的近似計算問題；約40年后，拉普拉斯建立了中心極限定理較一般的形式；到20世紀30年代，獨立和中心極限定理的最一般形式最終完成[5]。介紹科學發展史可以培養學生的理性思維；與此同時，為那些感興趣的學生提供繼續深入認識中心極限定理的渠道。

微課程中的第一個字——微，包含了兩層含義。一方面，微課程教學時間短，相對于傳統的課堂教學一學時50 分鐘時長而言，微課程視頻時長在10 分鐘左右甚至更短。另一方面，微課程教學內容少，一個微課程講授一個知識點。微課程時間短，更方便學生將碎片化的時間利用起來，這是微課程的特點和優點。但同時，微課程教學設計應避免將知識碎化，教學設計中更應加強教學完整性、系統性的考量。兩個中心極限定理微課程教學設計時，特別注意了合理設置課程結構。教學過程依據“案例引子→可視化展示→定理→應用于案例→小結”的結構；微課程結束部分安排了課程小結，注重了講授的完整性和系統性；定理和定理的應用兩部分時長占比超過70%，突出了課程的重點。此外，配以一定的輔助材料：練習題及其詳解和數值模擬時的程序代碼。