重視定義:數學新授課教學的用力點
——以“圓的起始課”教學為例
☉湖北省武漢市第四十五中學 葉 蓓
“圓的起始課”在不少版本的教材上都是通過生活中圓的圖片引入新課,進而給出圓的描述性定義,再給出“集合定義”,整節課中與圓相關的概念瑣碎,教學難有新意,往往還給出很多訓練知識記憶類的習題進行練習,這些“圓的起始課”教學的品質不高.最近筆者有機會執教“圓的起始課”,對比不同版本教材后“教材再建構”,基于深刻理解數學的角度重視圓的定義教學,并成為圓的新授課教學的一個用力點.本文梳理該課教學流程,并給出筆者的教后反思,供分享和研討.
一、“圓的起始課”教學流程
教學環節(一)畫圓活動,形成概念
教學組織:開課時讓學生用圓規畫出一個圓,并安排一個學生到黑板上畫圓,大家觀察在畫圓的過程中,圓是怎樣形成的,讓學生來說圓,從而生成圓的描述性定義.
設計意圖:通過學生的動手實踐,引導學生學會歸納,更注重數學中文字語言的精煉、簡潔,從而掌握好圓的描述性定義.
預設追問1:圓的位置和大小由什么決定呢?
教學組織:學生通過畫圓,得出圓的兩個要素——圓心和半徑.
設計意圖:通過學生的實踐,再次明確幾何圖形的位置和數量等決定性因素.
預設追問2:同一個圓中半徑的數量關系是什么?(學生回答“相等”,引出“一中同長”)
教學組織:通過圓中半徑的不變性,引出數學史“一中同長”.
設計意圖:加深學生對圓的描述性定義的理解.
預設追問3:到定點O等于OA長度的點有什么特點?
教學組織:引導學生復習角平分線的判定和線段垂直平分線的判定,并學會用點的集合來定義,從而得出圓的集合定義.
設計意圖:通過對角平分線和線段垂直平分線的判定,我們可以明確探究“圓的集合定義”,讓學生明白數學概念的一個重要方法——類比法.
預設講授:圓中還有很多相關概念,在小學也或多或少接觸過,現在我們再幫助同學們做一些梳理和明確,教師在圓上依次介紹弦、直徑、弧、等弧的概念及它們之間的相互聯系(直徑是特殊的弦,一條弦對著兩條弧,等弧必須在同圓或等圓中等).
跟進練習:如圖1,你能說出圖中哪些與圓有關的概念?
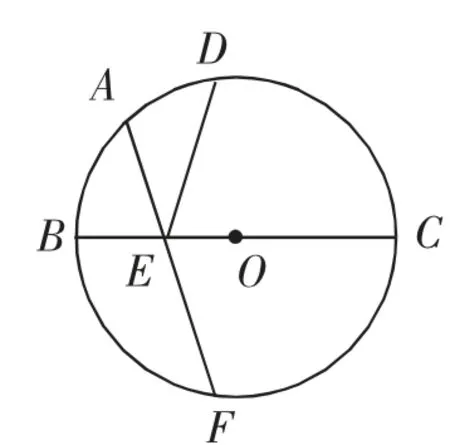
圖1

圖2
教學環節(二)典例分析,鞏固定義
例題:如圖2,矩形ABCD的對角線AC、BD相交于點O.求證:A、B、C、D四個點在以點O為圓心的同一個圓上.
教學組織:學生獨立完成后全班交流展示,教師點評并規范解題格式.
設計意圖:重在分析題目,題中已知矩形,要得到四點在同一個圓上,就是要得到這四個點到點O的距離相等,從而合理利用矩形的對角線相等且互相平分,做到所答即所問.
變式練習:如圖3,AC⊥BC,AD⊥BD,求證:A、B、C、D四點在同一個圓上.
教學組織:師生一起分析題中已知和求證,學生自己探討解題思路——點共圓的證法,反復強化學生“回到圓的定義去證題”的思想,進一步歸納出證明n個點到某點的距離相等是證明這n個點共圓的基本方法.

圖3
教學環節(三)圖形變式,生成新知
例題變式:如圖4,在AB邊上有點E,DB的延長線上有點F,請指出點E、點F與圓的位置關系.
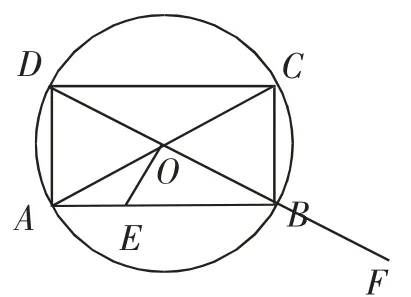
圖4
教學組織:在解決這個變式問題之后歸納出“在平面內,點與圓的位置關系有:點在圓內,點在圓上,點在圓外”,滲透數形結合的思想,并介紹等價符號“?”.
跟進練習:在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
(1)以C為圓心、3cm為半徑作圓,分析點A、B與圓的位置關系;
(2)以C為圓心、4cm為半徑作圓,分析點A、B與圓的位置關系;
(3)以C為圓心、2.4cm為半徑作圓,分析點A、B與圓的位置關系.
教學組織:教學時讓學生動手畫圓,分析三角形的頂點與圓的位置關系,第(3)問的數據2.4cm恰是斜邊上高的長度,為以后研究斜邊AB與該圓的位置關系預留了一個“數學現實”.
教學環節(四)師生小結,學習展望
小結問題1:本節課我們是如何學習圓的?你對圓的哪些概念印象深刻?
小結問題2:根據以往我們對一個新圖形的研究經驗,你覺得后續還會研究與圓相關的哪些內容?
教學預設:通過小結問題讓學生認識到圓的學習是從圓的定義(兩種不同定義)出發,梳理了圓的符號表示、圓的相關概念(如弦、弧等),并且利用圓的定義證明了矩形的四個頂點共圓.展望后續研究和學習,與圓有關的位置關系,基于圓的對稱性質的研究,與圓相關的運算等,都是學習的重點.
二、教后反思
教研組老師聽課之后對該課的教學表示了肯定,認為我們能夠“學材再建構”,從“教教材”走向了“用教材教”,并且在學程推進過程中,對能放手讓學生展示講解表示贊賞,認為這體現了以學生為主體的教學理念.當然,也有評課老師從理解數學的高度,對教學內容和教學方法提出一些建議,比如,要更加重視“從定義出發”的教學引導,重視“圓的定義”的教學.以下就圍繞如何重視“從定義出發”“回到定義”闡釋幾點教后反思.
(一)在“圓的定義”教學時要“慢”一點
當前由于所謂導學案的推動,不少新授課以“一個定義、三項注意、大量練習”的方式推進學程,這樣的教學方式敗壞了數學的名聲,把數學概念教學異化為習題教學、刷題教學,學生很難達到深刻理解數學概念的追求.就圓的定義教學而言,不少教師從生活中的圖片引入圓的概念,這類圖片中雖然有圓的形象,但是對引出圓的定義沒有多大幫助,而用圓規畫圓這個熟悉的操作,卻體現了圓的本質,所以在“圓的定義”教學時,慢下來,讓學生慢一點畫圓并感受圓是如何生成的,從而加深對圓的定義的概念性理解,為給出描述性定義做好鋪墊.
(二)在“圓的習題”教學時要“回到定義”
在數學新授課教學中,在概念生成之后,常常需要選用恰當的例、習題進行訓練,在組織學生練習之后,教師要講評,講評時可以適當追問學生對解題偏差、解題思路的理解,特別是要引導學生“回到定義”去解題.具體地說,當學生獲得思路貫通之后,教師可通過組織展示學生的步驟,基于“步步有據”解題追求,請學生回答依據,把圓的定義通過具體的題例讓學生反復表述,這也是回到定義去解題的具體操作要義.我們在上面的課堂教學中做得還不夠到位,值得今后改進和強化.
(三)在“小結展望”時要重視“從定義出發”
課堂小結時仍然可倡導本課研究的出發點是“圓的定義”,從圓的定義出發,就可把圓的要素(圓心、半徑)、相關概念(弦、弧等)進行梳理、結構化,完善結構化板書,并從與圓相關的性質進行學習展望,為后續學習提供方向和路徑.這里還可提及“結構化板書”在小結階段的操作要義,這就是把課堂教學進程中形成的一些板書(可能比較零亂、缺少條理)通過一些線段、框架線連接,形成“結構化板書”.

