初中數學中數形結合思想的應用研究
☉江蘇省無錫市梁溪中學 趙春蕾
數學學科與我們的日常生活聯系密切,更是物理、化學等學科的學習基礎.初中階段的數學教學起到了重要的過渡作用,對于學生的后續學習與發展意義顯著.在初中數學的內容體系中,“數”與“形”是基本的概念,數形結合的思想方法是培養、提升學生數學學科核心素養的途徑.本文以蘇科版初中數學為例,探討數形結合思想在實際教學中的應用.
一、數形結合思想的教學意義
1.簡化解題思路
在數學教學中,除了基本數學概念與原理,教師更需要強化對解題思路的講解,引導學生應用好數學思想方法,這是數學教學的核心,對于提升學生的數學應用能力及綜合素養具有重要的意義.在解決一些數學問題時,單純地從代數或者幾何層面進行思考難度較大,學生很難找到解決問題的突破口.這時可以嘗試使用數形結合的方法,對解答過程適當進行轉化,靈活變通,使得原本抽象的代數問題更加形象、具體,使得幾何關系不明顯的幾何問題更容易量化.通過轉換與簡化,能夠將原本復雜的方法、難以確定的數學問題變成學生所熟悉的題目,便于學生更好地理解題目、解答題目.
例如,有這樣一個問題:商場舉辦抽獎大酬賓活動,凡是購物滿200元的顧客都可以參與兩次抽獎活動.轉盤劃分為4個均等的區域,分別標上數字1~4,符合購物額度的顧客可以轉動轉盤2次,如果2次的數字之和為8或6,游客就能獲得獎品.那么顧客能夠獲獎的概率是多少呢?在解決這個問題時,由于還沒有接觸概率相關內容,因此教師無法嚴格地采用概率論的知識進行講解,單純地從代數運算角度展開思考,學生理解的難度較大,因此可以結合圖形,通過繪制樹狀圖,學生能夠將每一種可能的情況都考慮到,一共存在16種不同的抽獎情況,最后得到符合條件的情況共有4種,因此顧客獲獎的概率為25%.通過數形結合的方法,學生思考的過程得到了簡化,解題過程也更加直觀,學生能夠高效、準確地解決問題.
2.豐富解題方法
借助圖形輔助教學是初中數學教學的常用方法,在一些抽象、復雜的問題中應用廣泛,教師可以借助圖形將題目中的重要條件和信息展示出來.通過數形結合的方法,學生能夠直觀分析問題條件,選擇最適合的解題方法.在函數、方程等內容的教學中,采用數形結合的方法,能夠提高教學效率.
在“一次函數”教學過程中,部分學生對函數概念內涵的理解存在問題,無法靈活應用函數思維方法.比如,假設直線y=-2x+k和橫、縱坐標軸所圍成的三角形面積為9,那么參數k的值為多少?在分析這個問題時,學生能夠知道要求解什么,但是無法靈活應用已知信息進行求解.教師可以借助函數圖像法,將已知條件體現在圖像上,讓學生能夠直觀地分析已知條件,通過直線和坐標軸的交點構建方程,進而解決問題.
3.引導學生主動學習
數學學科本身具有抽象性與復雜性,學生學習起來困難較大.通過數形結合的方法,學生能夠將代數與幾何圖形結合起來,使得原本復雜的數學知識變得更加直觀,便于學生理解知識內容,學生的學習難度降低,學習積極性與主動性得到提升.當然,圖形方法雖然有直觀性等優勢,但也有其問題,即在計算方面沒有代數方便.因此,在解決數學問題時,除了要借助圖形來表征問題,同時要強化定量計算圖形信息的能力,綜合應用代數與幾何的解題優勢,發揮數形結合方法的效用,提升解題與學習效果.
例如,在“弧長與扇形面積”的教學中,需要通過代數運算的方法來計算扇形的特點,借助圖形的幾何意義能夠幫助學生更好地理解、掌握弧長公式,進而得到面積計算公式.通過這樣的數形結合方法,可以將數學問題變得更加簡單,學生學習的主動性得以加強.
二、數形結合案例解析
1.整式中的數形結合應用
整式運算是初中數學代數部分的基礎內容,通過數形結合的方法,可以實現數與形的對比,學生對整式的認知也更加直觀.
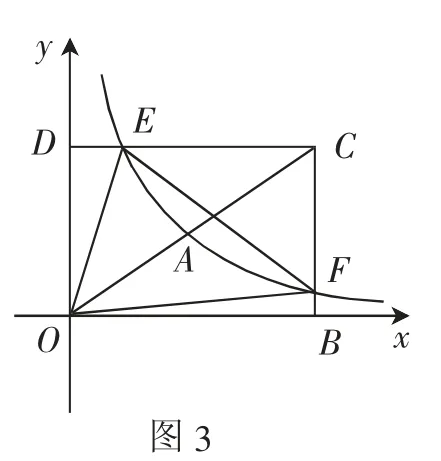
案例1:如圖1所示,正方形ABCD的邊長為3,以點A為圓心、2為半徑畫圓弧,以點D為圓心、3為半徑畫圓弧,試求解S1-S2的值.
解析:先求解出正方形的面積,然后利用扇形面積計算公式求出兩個扇形的面積,最后通過圖形關系,計算求出相應的值.
正方形ABCD的面積SABCD=3×3=9.
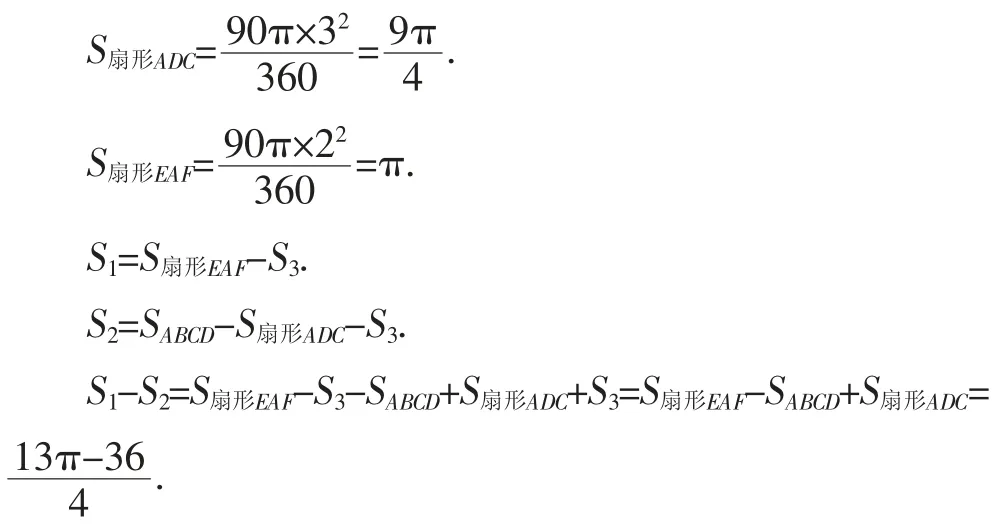
評析:本題考查的是整式的運算,通過與幾何圖形的結合,分析圖形關系所代表的整式運算過程.通過分析圖形的面積差,熟練使用整式的運算法則,進而解決這一問題.
2.平面坐標中的數形結合應用
平面直角坐標系是解析幾何的基礎,其內涵就是代數與幾何的聯系.在初中數學中,可以借助平面直角坐標系來解決圖形對稱等問題.
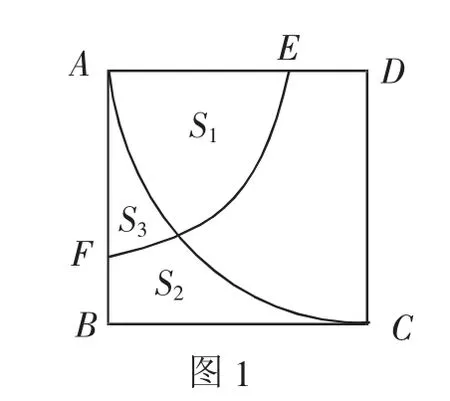
案例2:如圖2所示,△ABC經過一定的變換規則變為△A1B1C1.如果△ABC上有一點P,坐標為(x,y),試求△A1B1C1上對應的點P1的坐標.
解析:點P1是點P根據一定的變化規則移動過來的,因此要想確定點P1的坐標,就需要分析得到變換規則,這是解決這個問題的關鍵.觀察圖像可知,△A1B1C1是由△ABC向上平移2個單位,即橫坐標不變,縱坐標加2;然后以y軸為對稱軸進行軸對稱變化,即橫坐標變為相反數,縱坐標不變.因此,點P1的坐標為(-x,y+2).
評析:本題考查的是圖形變換,借助平面直角坐標系,可以直觀地反映坐標的變化,并且將坐標的變化用代數形式表達出來.
3.函數中的數形結合應用
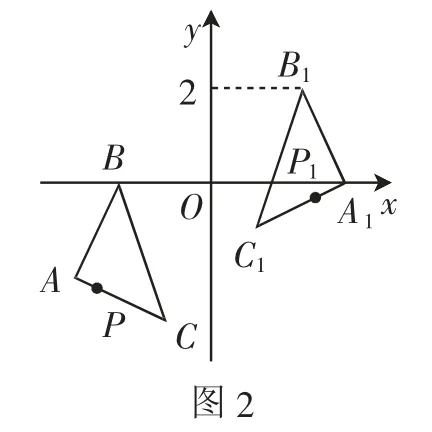
案例3:如圖3所示,在平面直角坐標系xOy中,四邊形ODCB為矩形,已知點D的坐標為(0,4),點B的坐標為(6,0).假設反比例函數y=,x>0,函數圖像經過線段OC的中點A,與DC交于點E,與BC交于點F.已知直線EF的解析式為y=k2x+b.
(1)求直線EF與反比例函數的解析式;
(2)求△OEF的面積.
解析:要想求解直線EF與反比例函數的解析式,關鍵是求解出點A的坐標.觀察函數圖像可知,△OEF的面積可以由矩形ODCB的面積減去△ODE、△OBF及△CEF的面積求得.
(1)易知點C的坐標為(6,4).
由點A是線段OC的中點,得點A(3,2).
則k1=6,得到反比例函數的解析式為
將x=6代入反比例函數的解析式,可得y=1,
則點F的坐標為(6,1).
將E、F兩點的坐標代入直線方程,計算可得k2=-,b=5.
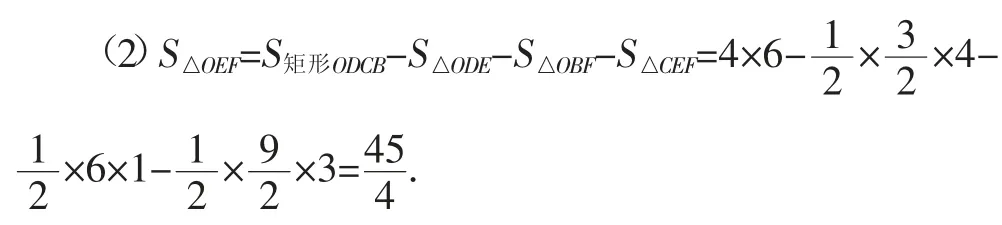
評析:本題的關鍵是聯立一次函數和反比例函數的解析式求解出交點的坐標,求解函數解析式的方法為待定系數法.
三、結語
綜上所述,在初中數學教學中,數形結合的思想方法具有重要的現實意義,有助于學生建立起幾何與代數之間的聯系,快速、準確地解決復雜的數學問題.在教學過程中,教師要科學評估學生的學習情況,引導學生使用好數形結合的思想方法,提升學生的數學知識應用能力與學科核心素養.

