基于問題解決的數學學習*

☉江西省南昌市二十七中學 翁 荔

希臘哲人德謨克立主張，教育力圖達到的目標并不是完備的知識，而是充分的理解.物理學家勞厄則進一步指出：“重要的不是獲得知識，而是發展思維能力.”問題解決的學習強調以問題為中心，通過解決問題來獲得知識、方法和思維.學生解決問題的過程就是思維的建構過程，它是學習范式的一種變革.基于問題解決的數學課堂以探索作為教學的生命線，在探索中理解數學，發現數學，對培養學生的創新意識和思維都有著十分積極的作用.

問題解決學習中最重要的教學支持是問題案例，這些問題案例就像“積木”一樣搭建學生完整的知識框架，教師及教學設計者要善于利用不同功能的問題案例幫助學生進行系統的學習.生長型案例的特點是以某一個容易達成的問題為基礎，其他問題按螺旋上升的方式展開，后一問題以前一問題為基礎，但在程度上比之前更深入，使前面知識不完善之處得到進一步的補充和豐富.下面就自己的實踐來談談個人對生長型案例的研究，不足之處請大家批評指正.

環節一：獨立思考，探求思路

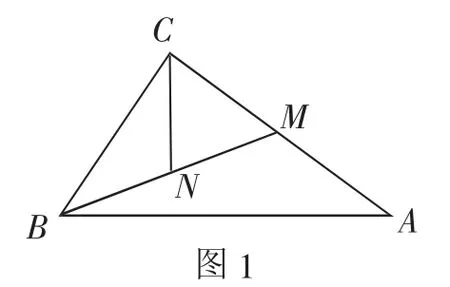
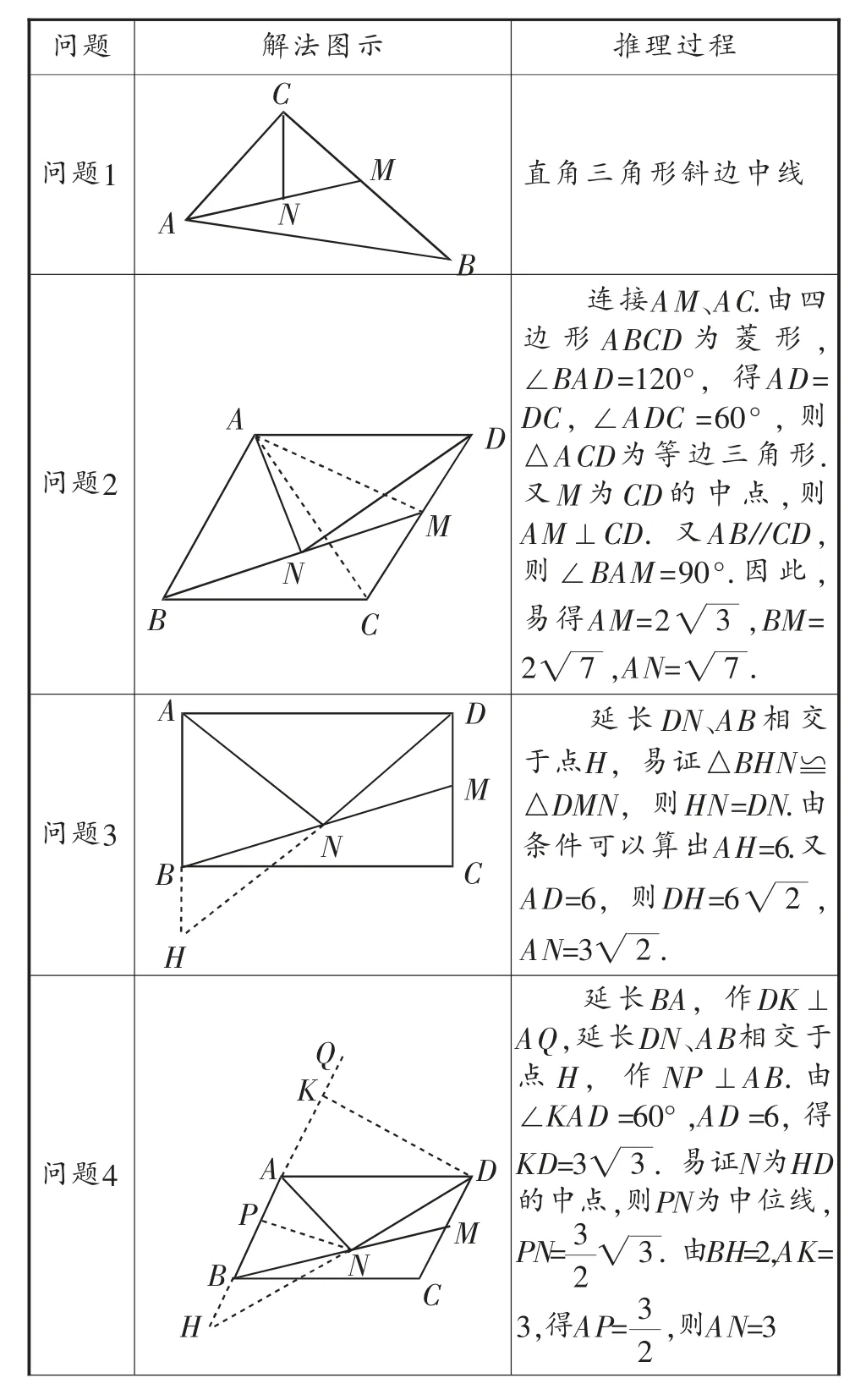
問題1：如圖1，在△ABC中，M是AC的中點，N是BM的中點，就稱CN是△ABC的“雙中線”，∠ACB=90°，AB=5，BC=3，求CN.

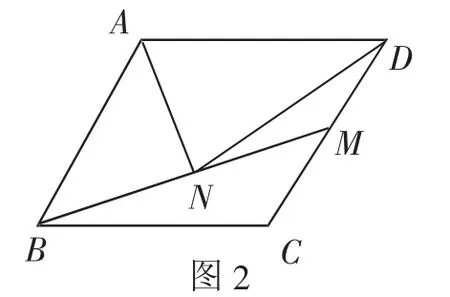
問題2：如圖2，M是菱形ABCD的邊CD的中點，N是BM的中點，則稱AN是菱形ABCD的“雙中線”，若AB=4，∠BAD=120°，求AN的長.

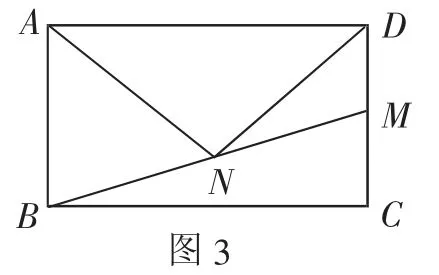
問題3：如圖3，AN是矩形ABCD的“雙中線”，若AB=4，BC=6，求AN的長.

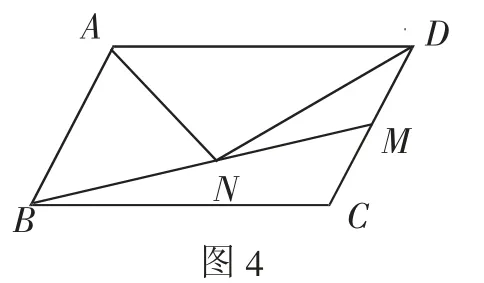
問題4：如圖4，AN是平行四邊形ABCD的“雙中線”，若AB=4，BC=6，∠BAD=120°，求AN的長.

這是一個以“雙中線”為背景的生長型案例，按照直角三角形→菱形→矩形→平行四邊形這樣的順序進行探究.首先，由學生獨立思考，在沒有老師和同學的指導下，發現自己真實的困惑.

環節二：小組合作，交流促進

學生在剛才獨立思考解決問題的環節中，會遇到許多“阻力”，這些“阻力”使他們在解決問題的時候沒有那么通暢.小組成員之間的相互合作，其實是相互意見的一種交換，彼此“互補”，形成了很多不同的解決方法.

問題1：獨立思考階段，大部分學生能完成，但有的學生完成不了，有以下幾種情況.（1）從點C向BM作垂線，構造直角三角形，把CN當作斜邊求解，但是得不到解題途徑.（2）把∠CBA也當作直角，用了兩次“斜邊中線等于斜邊的一半”.（3）使用勾股定理求解BM錯誤.

問題2：求解問題2，學生想出了很多解法，但是非常遺憾，雖然方法眾多，但是他們遇到了同一個“阻礙”，就是證明∠BAM=90°，有的是無法推理，有的是推理錯誤，下面列舉部分解法.

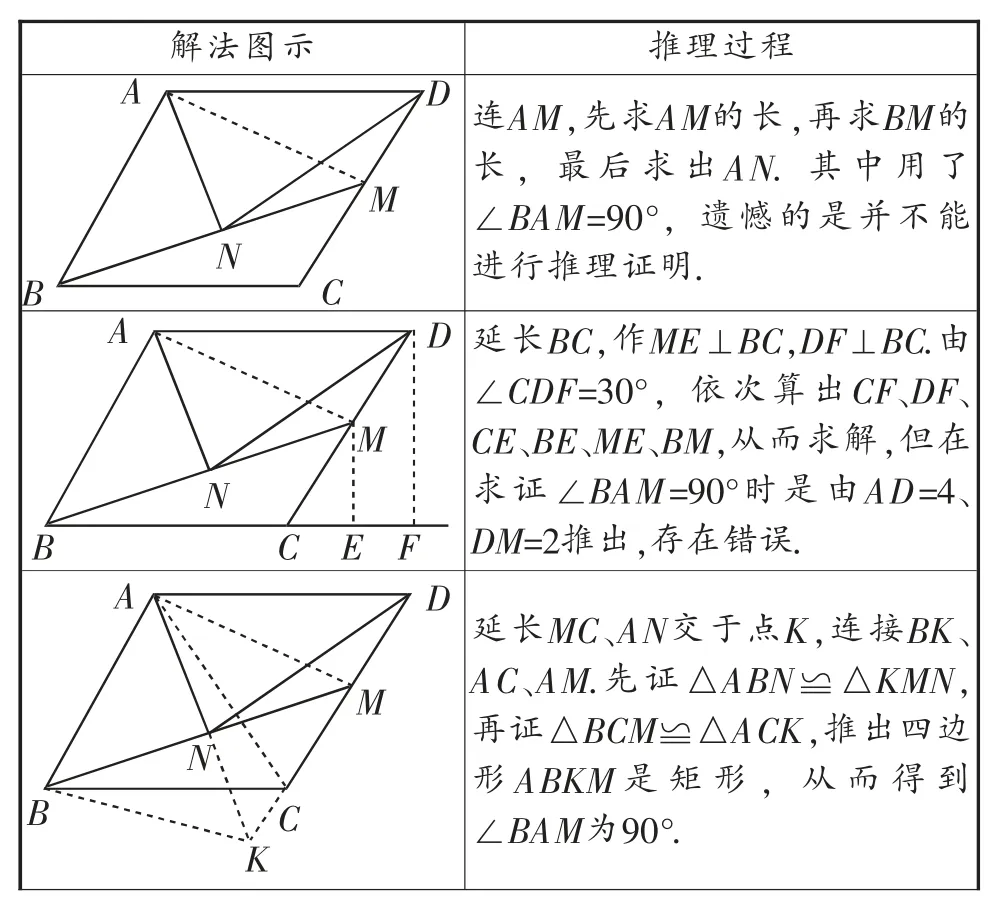
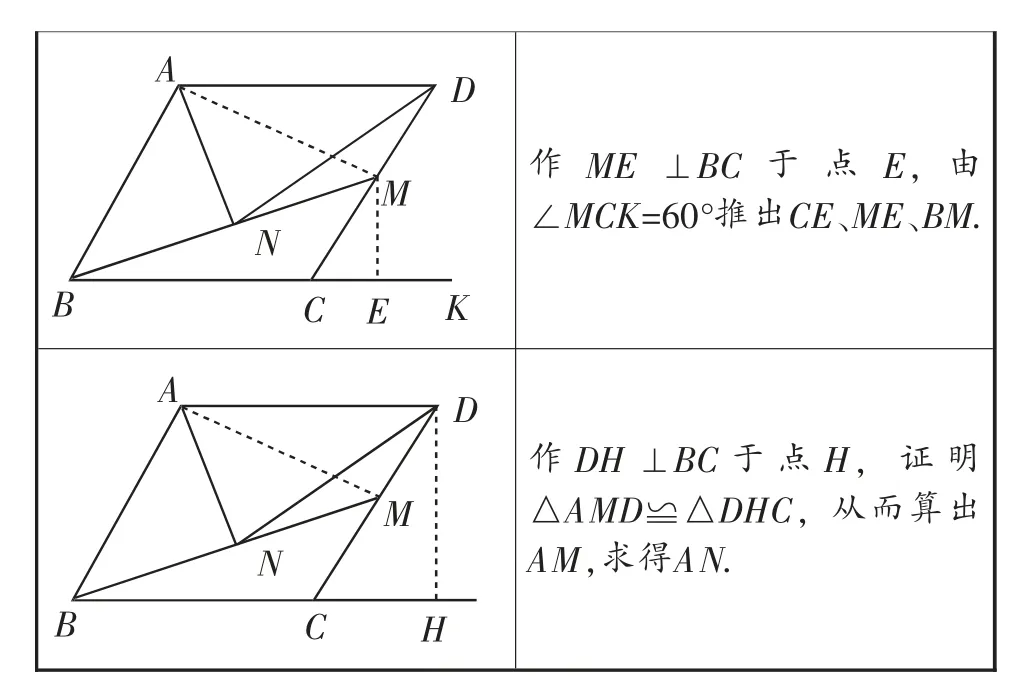
問題3：這一問題，很多小組成功解決了.現列舉部分解法.

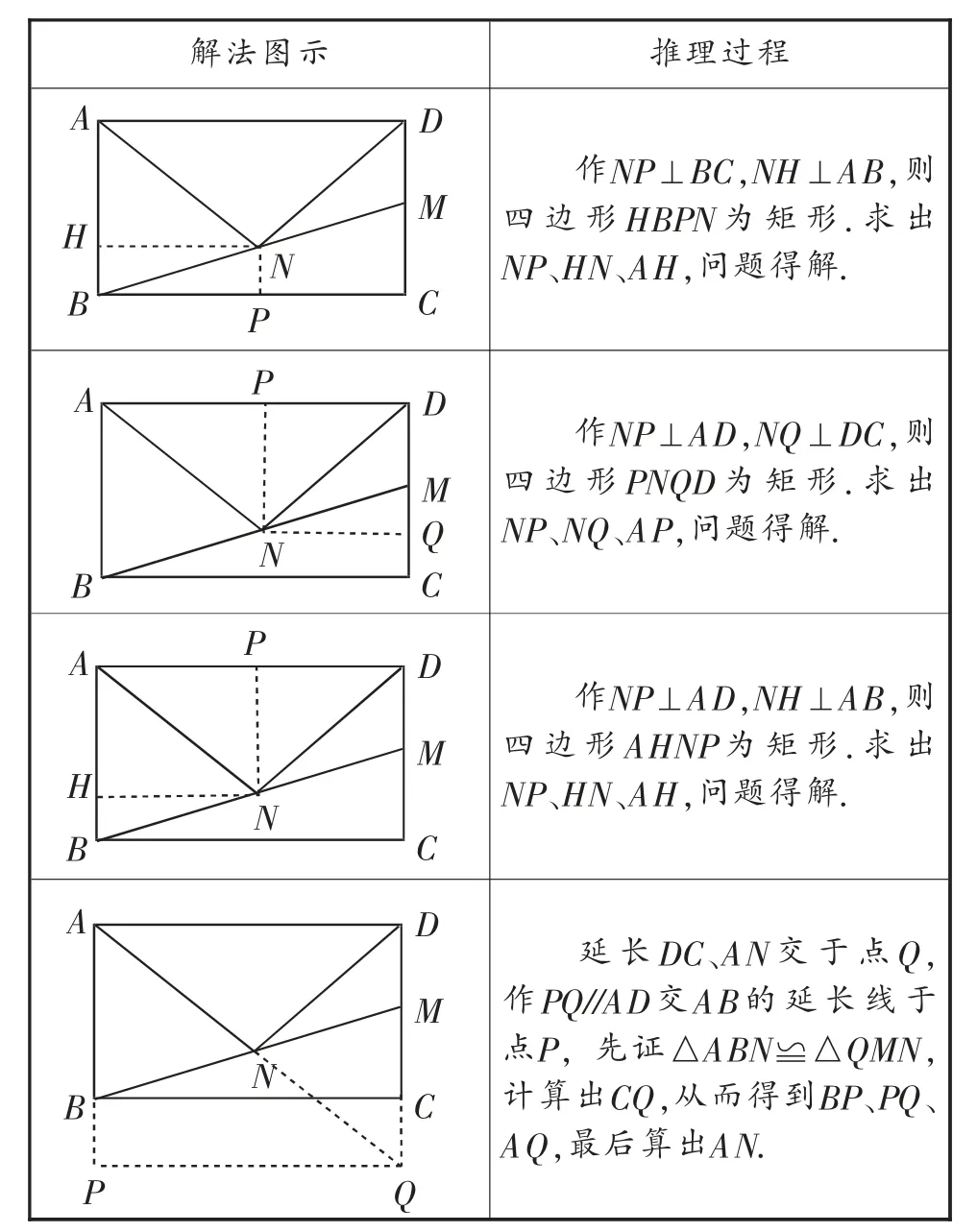
問題4：同樣部分小組解決了這個問題，可以說解法十分巧妙.

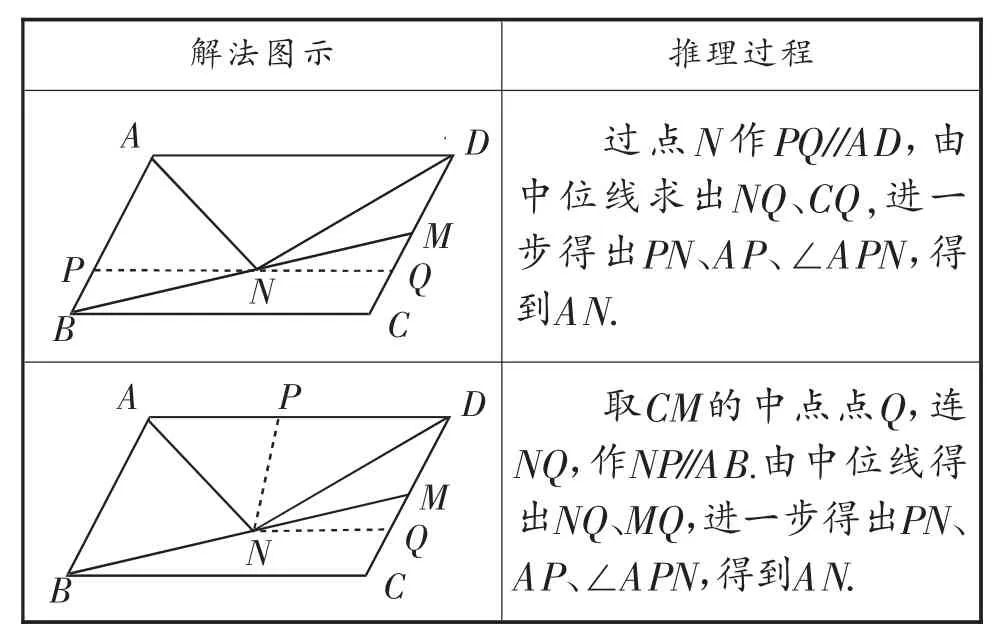
環節三：教師整理，完善結構

這一系列問題在圖形特征上有相似之處，即都涉及了兩條中線.那么，圖形上的相似能否帶來解法上的相似，類比完成呢？從與學生的交流中發現，他們都有這方面的嘗試，但都失敗了.為什么呢？歸根結底，還是對定理沒有全方位的認識.

問題1是整個解決問題中的源問題，其中兩條中線的作用，一條是利用中點求出線段一半的長，另一條的作用是和直角三角形結合，利用“直角三角形斜邊中線等于斜邊一半”來解決問題.問題2對比問題1的條件，兩中線依然存在，不同的條件是90°換成了菱形和120°，那么菱形和120°可否轉化成90°呢？問題3和問題4能否由之前的解題經驗獲得一些思路呢？根據學生的完成情況，教師提供了一組解法：

環節四：回顧總結，提升認識

首先肯定學生的“百花齊放”，在解決問題的時候發現了多種解法，有些解法充分體現了學生思維的廣闊性和靈活性，這一點，也是大家作為一個學習團體可以互相學習之處.

最后，根據學生的答題情況，引導大家思考如下問題，教師總結.

思考一：這節課大家討論了三角形和四邊形中的“雙中線”，結合以前的學習，由“中線”這個關鍵詞你能夠想到的解法有哪些？

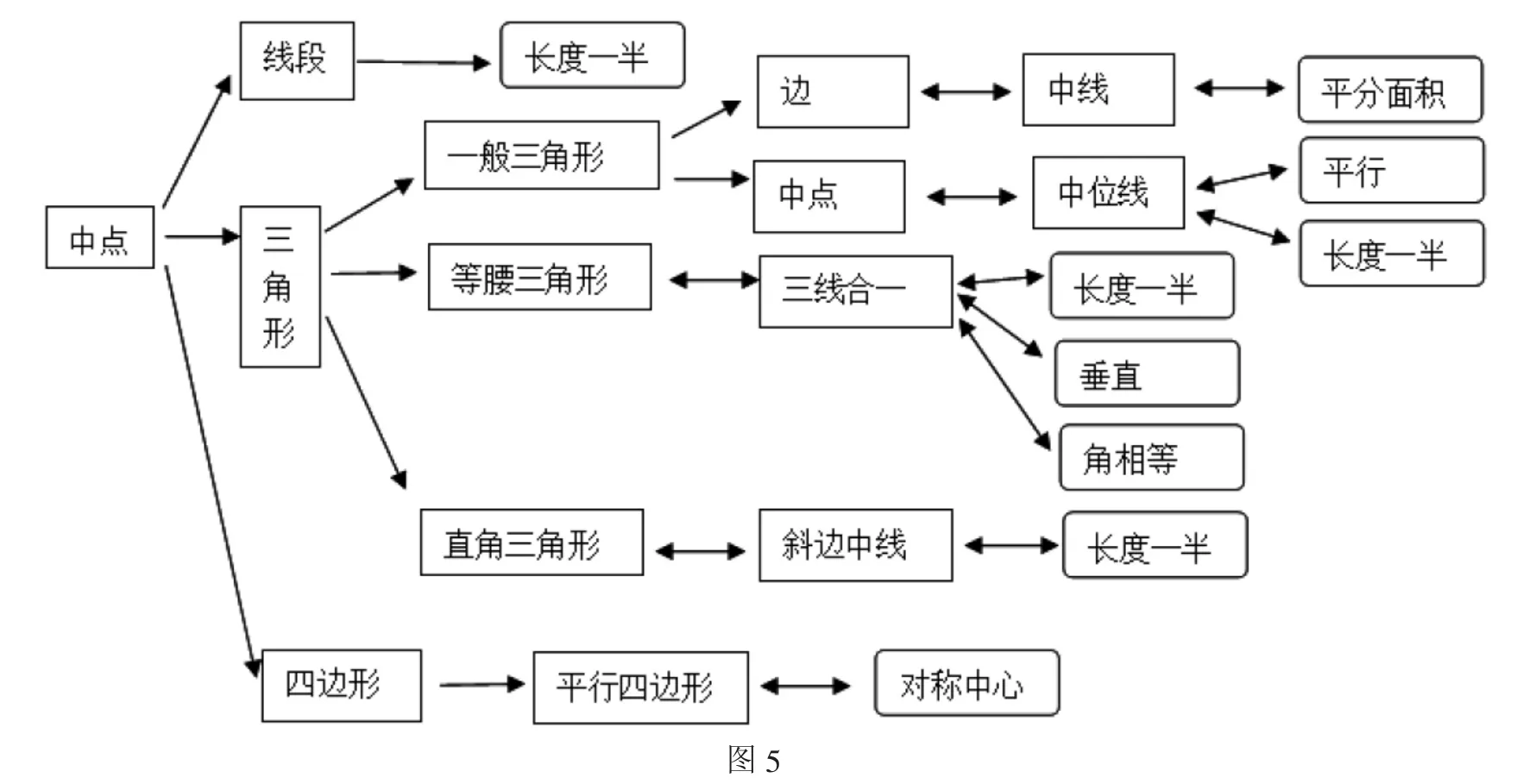
從學生的答題情況來看，由中點引發的求線段長的一半、構造中位線是學生圖示當中能夠存在并且容易激活的，但是直角三角形斜邊中線，是學生腦海中沒有的組塊，或者是處于較低的一級水平的組塊.通過這節課的學習，學生補充了原有圖示，使得圖示所表征的內容越來越細致、廣泛.教師和學生一起總結形成網絡圖，（如圖5）此圖仍需后續學習繼續完善.這節課的問題解決還涉及另一項能力的培養，就是識圖補圖.網絡圖中有雙向箭頭，從左到右的箭頭是形成解決問題所需要的命題系，從右到左的指向是識圖補圖的一種參照.

思考二：今天的問題解決中出現了120°，你認為它發揮了什么作用？你覺得像這樣能夠促進問題解決的特殊角還有哪些？

對于“特殊角”，在學習了勾股定理之后，學生在解題中經常會遇到30°、45°、60°這樣的特殊角，但對120°、135°、150°這三個鈍角并不是很熟悉，這三個角其實是60°、45°、30°角的補角，可以轉化成這三個特殊角.同時，120°=30°+90°，135°=45°+90°，150°=60°+90°，這也是這三個鈍角能夠在直角三角形中發揮作用的關鍵.另外，學生也想到22.5°、15°分別是45°、30°的一半，也是特殊角.

思考三：在問題4的解決中，兩組學生用了簡單巧妙的方法，想想看，如果把問題4中的邊長由6換成8，還能用此方法嗎？在教師提供的解法中，問題1、2、3都用了直角三角形斜邊中線解決，問題4沒用，是哪些條件不滿足導致的？

學生的解法其實是針對特殊問題的特殊解法，并不通用，要讓學生意識到這一點.教師的解法沒用斜邊中線，而是另辟蹊徑，原因是斜邊中線和直角很難同時存在，這一問題的解決加強了學生對定理運用的靈活性.

理解數學知識、提高思維能力、學會思考問題，是數學教學的核心目標.這就要求教師把這三者融入到教學中，使學生成為善于認識問題和解決問題的人.這節課是圍繞“雙中線”展開的一節中考復習課，問題從簡單的圖形開始，逐步深入.主要目的是加強所學知識的深度和廣度，力圖達到多角度理解知識，多方位聯系概念.

教學的目的不是讓學生強記解法，也不是大搞題海戰術，要讓學生把具體的知識忘掉以后，頭腦中還能剩下數學的東西，就需要教師的精心設計與有針對性的深化，這無疑為問題解決的教學提供了一個很好的模式.