一道中考幾何壓軸題的多種證法與教學啟示

☉重慶市萬州高級中學 張 進

一、試題呈現

（2018年龍東中考題）如圖，在Rt△BCD中，∠CBD=90°，BC=BD，點A在CB的延長線上，且BA=BC，點E在直線BD上移動，過點E作射線EF⊥EA，交CD所在直線于點F.

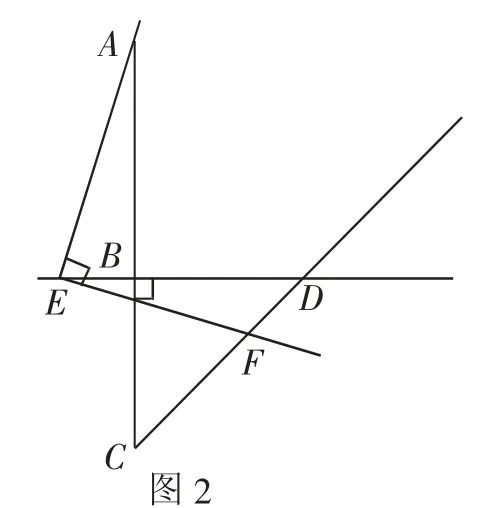
（2）當點E在直線BD上移動時，如圖2、圖3所示，線段BC、DE與DF又有怎樣的數量關系？請直接寫出你的猜想，不需證明.

二、思路探究

三、解法探究

1.關于第（1）問的解法探究

思路1：利用直角，構“三垂直”.

證法1：如圖4，過點F作FG⊥BD于點G.

所以∠EGF=∠ABE=90°，則∠BAE+∠AEB=90°.

因為EF⊥EA，所以∠GEF+∠AEB=90°.

所以∠BAE=∠GEF.

因為BC=BD，BA=BC，所以AB=BD.

因為∠CBD=90°，BC=BD，所以∠CDB=∠FDG=45°，則

思路2：洞察結構，構“輔助圓”.

證法2：如圖5，連接AD、AF.

因為BC=BD，BA=BC，∠CBD=90°，所以△CBD、△ABD均為等腰直角三角形，則∠ADF=90°.又因為EF⊥EA，所以A、E、D、F四點共圓，⊙O的圓心O即為AF的中點，所以∠EAF=∠CDB=∠BAD=45°，即∠BAE+∠EAD=∠EAD+∠DAF，所以∠BAE=∠DAF.

思路3：巧妙截取，構造全等.

證法3：如圖6，在AB上截取AG=ED，連接EG.

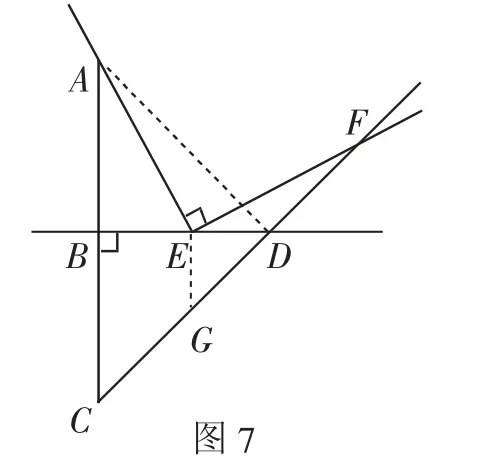
證法4：如圖7，連接AD，過點E作EG⊥BD交CD于點G.

證法5：如圖8，連接AD，過點E作EG⊥BD交AD于點G.

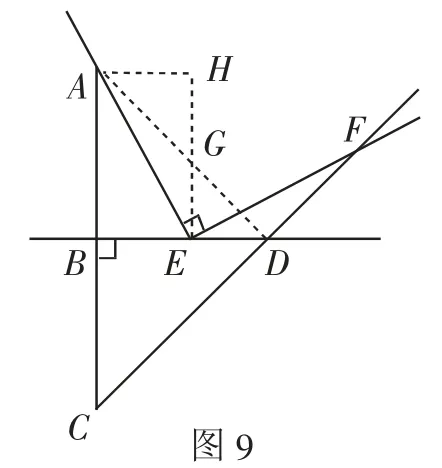
證法6：如圖9，連接AD，過點E作EG⊥BD交AD于點G，過點A作AH⊥EG交EG的延長線于點H.

思路4：巧妙對稱，構造等腰.

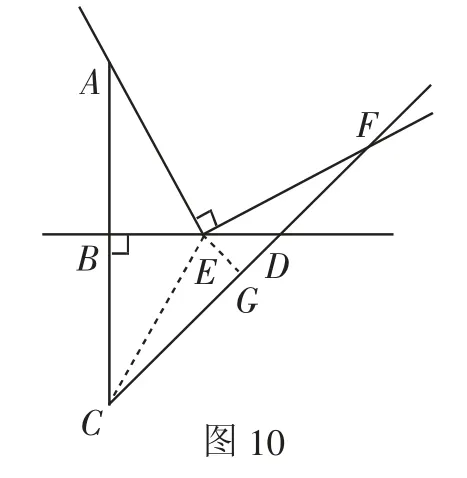
證法7：如圖10，過點E作EG⊥CD于點G，連接CE.

易證△EGD、△CBD為等腰直角三角形，然后證明△ABE△CBE（SAS），再證△ECG△EFG（AAS），則FG=CG.

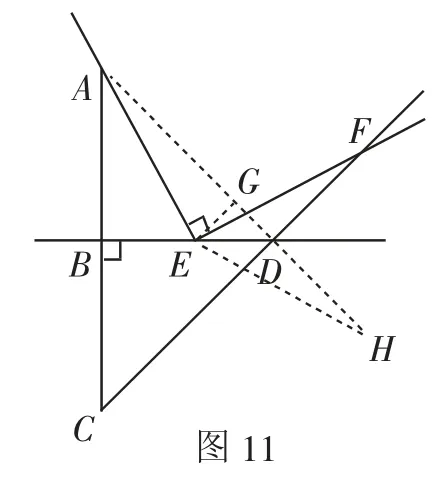
證法8：如圖11，連接AD并延長至點H，使DH=FD，連接EH，過點E作EG⊥AH于點G.

證法9：如圖12，連接AD并延長至點G，使DG=FD，連接EG、FG.

思路5：巧妙旋轉，構“特殊形”.

證法10：如圖13，在BC上截取BG=BE，連接EG、DG.

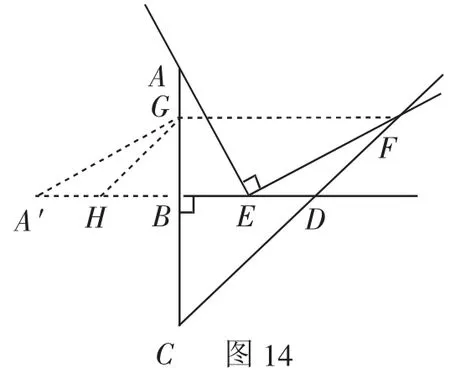
證法11：如圖14，過點F作FG∥BD交AB于點G，過點G作GA′∥EF交DB的延長線于點A′，過點G作GH∥FD交A′B于點H.

證法12：如圖15，過點D作DG⊥BD，使DG=ED，連接EG、AD，過點G 作GH∥AE交AD于點H.

證法13：如圖16，連接AD，過點E作EG⊥AD于點G，過點E作EH⊥CD于點H.

證法14：如圖17，過點A作AM⊥AB，過點D作DM⊥BD于點D，在AM上截取MG=MN，連接DG、NG.

思路6：用代數法，求解直角三角形.

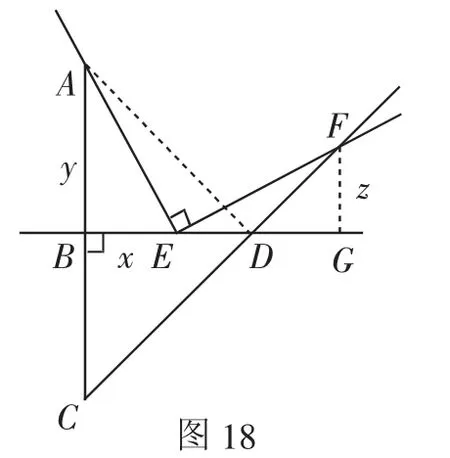
證法15：如圖18，過點F作FG⊥BD于點G，連接AD.

因為EF⊥EA，所以∠DEF+∠AEB=90°.又∠BAE+∠AEB=90°，所以∠BAE=∠DEF，則tan∠BAE=tan∠GEF，所以，整理得（y-x）（x-z）=0.因為y≠x，所以x=

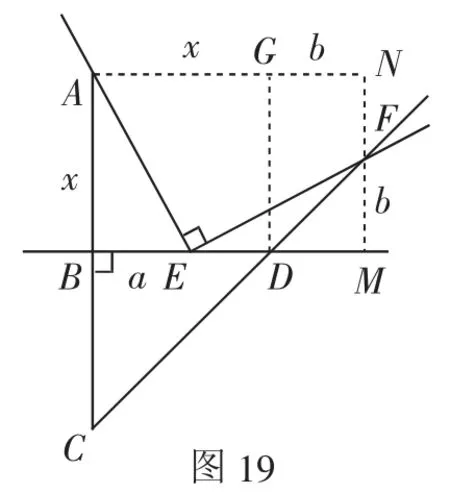
證法16：如圖19，連接AF，過點F作MF⊥BD于點M，過點A作AN⊥AB交MF的延長線于點N，過點D作DG⊥AN于點G.

可得矩形ABMN和正方形ABDG.

設AB=x，BE=a，FM=DM=GN=b，則FN=x-b，EM=x+b-a.

根據勾股定理，可得AF2=AE2+EF2，AE2=AB2+BE2，EF2=EM2+FM2，AF2=AN2+FN2，所以（x+b）2+（x-b）2=（x+b-a）2+b2+x2+a2，整理并化簡得a=b，即BE=FM=DM，所以

2.關于第（2）問圖2、圖3的解法探究

借用第（1）問的解題方法，采用類比推理的辦法可探究圖2的結論為圖3的結論為BC+限于篇幅，不再贅述.

四、教學啟示

1.提倡一題多解，開闊解題視野

幾何壓軸題教學時，教師要深刻理解問題結構和圖形結構的變化情況，要善于抓住題目中的條件特征、數字特征、結論特征和圖形特征，從中尋找解題突破口，聯系相關知識點和解題方法，就可以得到不同的解法，這就是數學上常說的一題多解.數學解題教學中，教師應該有意識地針對一些典型的課本習題、中考試題，引導學生嘗試運用不同的方法去解決，有利于溝通知識的內涵和外延，尋找自然解法.一題多解的目的并不在于“多解”，而在于培養學生思維的靈活性和層次性，這樣就可以拓寬學生的解題思路，克服思維定式，培養學生的求異思維能力，開闊學生的解題視野.

2.學會類比推理，提高解題效率

三角形和四邊形是初中數學的重要考點，在數學解題過程中，有很多幾何壓軸題可通過類比推理的方法解決，以達到高效、快捷的效果，激活學生思維，提高解題效率.類比推理是根據兩個對象之間的形同和相似進行推理論證的一種重要數學思想方法，是中學數學解題中的重要方法之一，通過類比推理能夠尋求解決同類問題的思路，可讓模糊的問題清晰化、復雜的問題簡單化、隱性的問題顯性化.初中數學內容廣泛，很多內容如代數問題、幾何問題、方程和函數問題都需要用到類比推理.類比推理是一種行之有效的數學解題方法，在初中數學中大膽運用類比推理，不但可以達到溫故而知新的目的，而且可以培養學生的靈活性思維，使復雜、抽象的數學問題簡單化，從而大大提高解題的效率和速度.

3.構建基本模型，提升數學素養

在平時的解題教學中，教師幫助學生提煉總結出一些常見的幾何基本模型，并運用這些基本模型解題，不僅有助于激發學生的學習興趣，提高解題效率，而且對發展數學思維能力、培養創新意識具有重要的現實意義.重視基本模型解決幾何題的一個基本套路，首先要認真分析條件，將條件與相關“基本模型”結合起來，利用這個“基本模型”的性質獲得相關的結論，有時，背景圖形中不一定有與條件匹配的“基本模型”，這時需要聯想相關知識添加輔助線構造出相關的“基本模型”，再利用這個“基本模型”的性質，獲取相應的結論，達到解決問題的目的.教師在平時教學中指導學生尋找解題思路，要熟悉基本模型，多總結、多積累、多識記、多聯想、多應用，形成基本的解題能力，積累基本的數學活動經驗，徹底脫離“題海戰術”，努力提升學生的數學素養.