小學數學教學中轉化思想的滲透分析
石開勇
摘 要:小學數學的學習需要轉化思維,因此數學教師要通過新舊知識相互穿插,形成轉化意識;合理運用假設方式,助推學生思維進行轉化;數形轉化的應用,創新思維模式,進而提高小學生的數學學習能力。
關鍵詞:小學數學教學;轉化思想;的滲透分析
數學知識的抽象性是眾所周知的,而對于小學生來說,要學習這種抽象性強的知識,必須具備一定抽象思維和邏輯思維,但是小學生的邏輯思維還不是很活躍,形象思維則比較活躍,因此小學數學教師要想一些辦法,幫助學生轉化數學知識,形成轉化思維,以此更好地學習數學知識。在小學數學教學中,教師滲透轉化思想,幫助學生快速解題,提高學習效率。數學教師運用各種方式,訓練學生的轉化思維,從而促進學生全面發展。
一、新舊知識相互穿插,形成轉化意識
新知識的學習,是在舊知識掌握的基礎上,通過新舊知識的穿插,能夠更好地強化學生對已經掌握知識的激活,形成新舊知識之間的練習,運用已經掌握的知識,轉化成為新的知識,從而形成轉化意識,逐漸形成轉化思維。如同幾何知識的學習,小學數學教材內容涉及到很多圖形幾何知識,各種圖形的面積,會逐漸學習到長方形、正方形、三角形、平行四邊形、梯形等圖形面積的計算方法。在學習的過程中,教師需要將長方形面積公式作為基礎,將其貫穿在其他圖形面積公式的教學中。長方形面積公式則是非常重要的內容,將其引入到其他圖形面積公式的教學中,體現出了轉化思想。數學教師運用轉化教學:多媒體上展示平行四邊形,由很多小方格組成,引導學生數一數有多少個小方格?每一個小方格是1平方米,不滿一格的均按半個計算,問這個平行四邊形的面積是多少平方米?學生數完后,得出平行四邊形的面積是24cm2。然后展示出一個長方形,也由小方格組成,讓學生數一數并算一算長方形的面積是多少,學生數完得出長方形長為6cm,寬為4cm,面積是24m2。問學生:你發現了什么?學生通過比較、討論,得出:兩個圖形的底與長,高與寬和面積分別相等。在多媒體上,展示出平行四邊形變成長方形的推導過程,然后并讓學生拿出自己的學具平行四邊形紙片,像剛才演示的操作一樣,同桌相互合作,動手進行剪、拼、移的操作方法,從中再次驗證一下是否正確,教師巡回指導學生的操作。同時引導學生思考:通過剛才的操作演示你發現了什么?學生可能會回答:我發現把平行四邊形的面積轉化成長方形后形狀變了,但面積沒有變,即長方形面積就等于平行四邊形面積。同學發現長方形的長就是平行四邊形的底,寬就是平行四邊形的高,進而引導學生利用長方形的面積公式,推導出了平行四邊形面積的計算公式,平行四邊形的面積=底×高。
二、合理運用假設方式,助推學生思維的轉化
小學生學習數學時,受到數學知識邏輯性的影響,當學生遇到一些比較有難度的問題時,自己不知道該用什么樣的思維解決這些問題,也就停止了學習腳步。所以,小學教師組織教學活動的時候,要運用合理的方式,幫助學生形成轉化思維,將抽象的問題,轉化成為具體的問題,通過假設的方式,讓學生掌握到問題中的重點,讓學生找到解題的入口,掌握問題重點,才能快速地解決問題。比如,速度問題中,問題是小紅和小美進行賽跑,他們所用的時間是一樣的,路程也是一樣的,但是兩個人的速度不同,小紅比較快,小美比較慢,小紅的速度比小美的速度快20%,小美則比小紅的速度慢30%,請問兩人跑步的速度分別是多少?在沒有具體時間和路程的情況下,學生們在解決這個問題時,有些手足無措,但是教師運用了假設的方式,提出一些假設條件,然后解答出問題的答案。假如說兩個人所跑的路程都是500米,這樣就將抽象的問題,變成的具體的問題,學生會算出答案。借助假設的方式,解答數學邏輯問題,轉化思維的作用凸顯出來,問題具體化、簡單化,學生理解起來就更加容易。
三、數形轉化的應用,創新思維模式
具體的、形象的思維,是小學生思維特點,因此在教學中滲透轉化思維,教師要能運用具體事物將數學抽象知識表現出來,數形轉化就是非常好的代表,將數字通過具體的形狀或者形體展現在學生面前,從而幫助學生理解數學問題或者知識,把復雜數量關系,轉化成簡單的形象問題,這一過程就是轉化的過程,學生理解起來更加容易,進而提高解題速度。
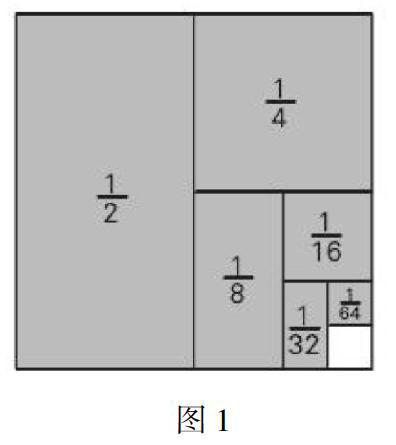
例如,分數的計算中,在一連串分數的計算中,教師可以運用數形轉化的思想,通過圖案將每個分數表示出來,方便學生們理解,讓一些抽象的數字變得具體化,以新穎的方式展示給學生,學生固有思維模式被打破,也有利于培養學生的創新思維。像1/2+1/4+1/6+1/8+1/16+1/32+1/64,將這些數用一個正方形表示出來,如圖1,陰影部分就是和,就整個正方形,看成是單位1,減去空白部分1/64,也就是63/64。這種轉化思維的滲透,不但提高了解題速度,還培養了學生創新能力。
結束語:綜上所述,小學數學中教師要逐漸滲透轉化思維,通過合理的方式,幫助學生形成轉化思維,進而形成數學學習意識,提高學習能力,全面地發展。
參考文獻:
[1]李桂芹.小學高年級數學教學中轉化思想的滲透與運用[J].數學學習與研究,2018(20):80.
[2]廖秀芳.教有所思 學有所想——轉化思想在小學數學教學中的滲透[J].福建基礎教育研究,2018(06):86-87.

