數感的“生態”教學嘗試
——以《二次根式的加減》教學為例
南京師大附中新城初級中學黃山路分校 張 潔
在《二次根式的加減》教學過程中,聯想到2016 年劉乃志特級教師在鎮江的一節展示課,課上使用了面積為8 和18 的兩個正方形引入二次根試的加減法問題,當時筆者想如果劉老師止步于列出加式,對于大部分同學們能不能靠自己的感覺,成功地化簡兩個二次根式并發現二次根式合并的方法呢?通過教學實踐,發現大部分學力較優的同學是可以做到的,那這節課我們該如何上才能讓大部分孩子有所收獲呢?對此,筆者在課堂上進行了相應實踐。嘗試如下:
一、教學過程
1.數感在嘗試中“孕育”
活動1 如圖1,由低到高的三個正方形的面積分別是2,8 和18,試計算三個正方形的邊長之和。
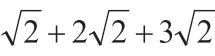
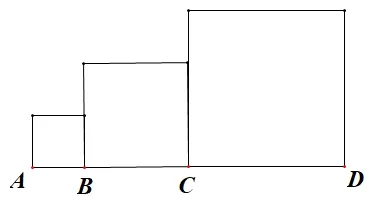
圖1
2.數感在思辨中“生根”
問題1 請試著再舉幾組通過加減運算可以合并的二次根式,要進行二次根式加減運算,它們具備什么特征才能進行運算?
設計意圖:通過同學們舉例,說明依據這樣的特征舉例的,從每一組具體的可以合并的二次根式中歸納出怎樣的二次根式可以合并,即同類二次根式的概念。借助多次追問,能啟發學生主動反思自己的學習過程,積極探尋知識的內核。
想一想:在下列二次根式中是同類二次根式的有哪些?

設計意圖:通過找同類二次根式,進一步明確同類二次根式的特征。本處設計了兩個帶有字母的同類二次根式,為下面帶有字母的二次根式的加減運算作鋪墊。
設計意圖:再次讓同學們嘗試計算,進一步類比合并同類項,在計算過程中梳理二次根式加減法的運算步驟。
問題2 通過剛才的計算,你能試著說出怎樣進行二次根式加減嗎?
設計意圖:學生通過運算,總結運算過程中發現的二次根式的加法法則。
3.數感在應用中“發芽”
例1 計算:
設計意圖:三道計算各具代表性,通過本組訓練題,進一步鞏固和深化同類二次根式的概念,運用二次根式相加減的法則進行化簡和計算,進一步形成運算能力,提升數學素養,加強交流,讓思想充分碰撞,促進生生的共同發展。
例2 如圖2,兩個圓的圓心相同,半徑分別為R、r,面積分別是27 cm2、3 cm2。求圓環的寬度(兩圓半徑之差)。
設計意圖:在解決實際問題過程中,感受二次根式加減法的必要性。
拓展提高:當a取什么值時,二次根式和是同類二次根式?
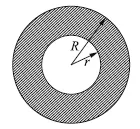
圖2
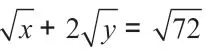
4.數感在反思中“成長”
引導學生本節課中的定義、法則和方法三個角度回顧反思。
二、教學反思
1.何時形成同類二次根式的概念
同類二次根式是進行二次根式加減運算過程中的“產物”,是在二次根式加減過程中,為了判斷“什么樣的二次根式可以通過加減合并”得到同類二次根式,沒有此概念也不影響“二次根式加減法”知識體系的形成。因此將同類二次根式概念放在新課開始較為突兀,可以讓學生獨立嘗試計算時,讓同學們感知需要引入一個名詞來描述 “化簡后,被開方數相同” 的二次根式,再引入同類二次根式概念,水到渠成。
2.在情境問題中是直接憑“意識”計算,還是列式后戛然而止
通過教學實踐,對于大部分同學都可以通過聯系二次根式的化簡,獨立嘗試,得到運算結果,剩下的也可以通過教師引導得到結果,只不過計算過程中“意識”占了主導,教師沒有必要打破他們合理的“感覺”,重建概念。可以順勢而為,理清計算依據,反思計算方法,構建運算法則。這樣過程體現了運用數字和運算法則進行靈活運算的能力,同時也體驗培養其積極的學習態度與信心。這樣的概念形成過程也是數感“生根”的過程。
3.基于數感的教學必要性
《數學課程標準》明確地把數感作為數學學習的內容之一提出來,要求初中生“建立初步的數感和符號感”。簡單而言,數感是我們對數字關系和數字模式的意識,以及運用這種意識靈活地解決數字問題的能力,學生具有“數感”的典型特征就是他們能夠對其所面對的數字模式、數字關系和計算過程進行歸納,并能夠把新知識和已有知識聯系起來。
教學中不妨將學生學習中已產生的這種意識,應用于新知的學習。像有理數的運算律引入,解一元一次不等式等,根據學生的經驗和感悟,完全可以得到相應的結論,在此基礎上對結果的形成過程進行追問和反思,也是建立和運用數感的重要過程。通過一次次“追問”,一次次地“思考”,學生的數感亦在初獲結論時“孕育”,在思辨結論時“生根”,在應用結論時“發芽”,在反思結論中“成長”。

