立足通性通法 尋求解題策略
——含參函數單調性分類討論的標準
安徽省樅陽縣會宮中學 (246740) 方明生
近幾年的全國卷,導數均以壓軸題的身份出現,難度教大,學生的得分普遍較低,讓不少學生望而生畏.不管是求極值、最值、不等式證明還是函數零點的個數問題,最終都會涉及到含參函數的單調性,而正是這個參數“嚇退”了我們的學生.追起根源,我們會發現含參函數的單調性問題的本質其實就是解含參的一元一次不等式、一元二次型不等式.而含參不等式的解法亦是高中不等式題型的難點,大部分學生根本把握不好分類討論的標準,容易出現重復或者遺漏.通過筆者多年的教學,對此類題型形成了一點自己的見解,今天寫出來供大家參考,不當之處請方家指正.
一、一元一次不等式型
例1 設函數f(x)=xekx,求f(x)的單調區間.
解:由題意可得f′(x)=ekx+kxekx=ekx(1+kx),易知ekx>0恒成立.
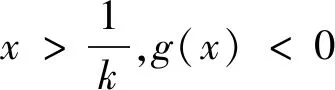
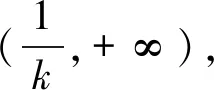
評注:原題求導后轉化為求解不等式g(x)>0和g(x)<0,因為在解不等式過程中要將參數k除到右邊,根據不等式的性質,此時就需要對k的正負進行討論.故一元一次不等式討論的標準是:(1)對一次項前的系數分正、負和零進行分類討論;(2)在系數為正(或負)的情況下判斷根是否在定義域內,從而進一步展開討論.
二、一元二次不等式型

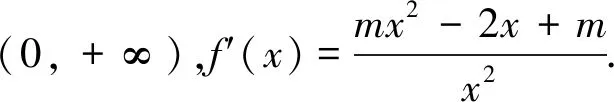
(1)當m=0時,f′(x)=-2x<0恒成立,所以f(x)在(0,+∞)上單調遞減.
(2)當m>0時,函數g(x)開口朝上,Δ=4-4m2(對判別式正負進行討論).
(ⅰ)當Δ≤0時,即m≥1,此時f′(x)≥0恒成立,故函數f(x)在(0,+∞)單調遞增.
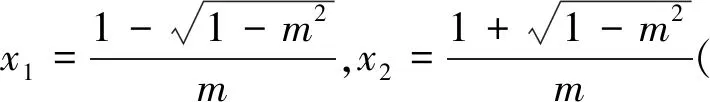
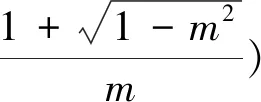
(3)當m<0時,(此步易判斷f′(x)<0恒成立,考慮有部分學生做題時不善于去發現規律,故而筆者依舊按照對應的解題步驟去完成)函數g(x)開口朝下,Δ=4-4m2.
(ⅰ)當Δ≤0時,即m≤-1,此時f′(x)≤0恒成立,故函數f(x)在(0,+∞)單調遞減.
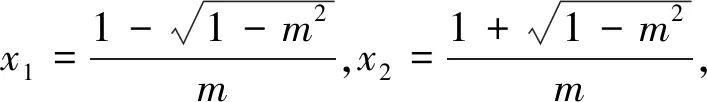
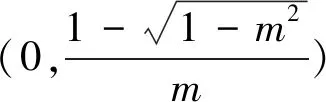
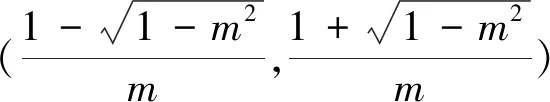
評注:本題求導后進行通分,分母恒為正,故而不需要考慮分母的正負.解一元二次不等式關鍵在于二項式系數的正負討論(學生容易忽略為零的情況)、根的存在以及根的大小.例2的討論標準是對系數的正負以及判別式進行的討論.
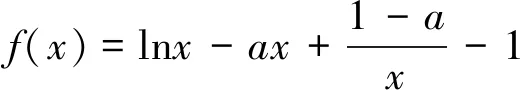
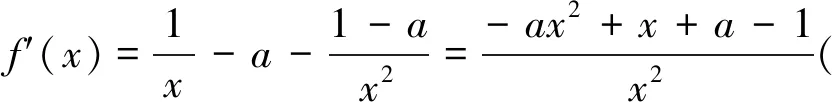
令g(x)=-ax2+x+a-1.
(1)當a=0時,g(x)=x-1(一次函數).令g(x)>0得到x>1;令g(x)<0,得0 (2)當a>0時,二次函數g(x)=-ax2+x+a-1的開口朝下,Δ=1+4a(a-1)=(2a-1)2≥0,所以g(x)=-(x-1)[ax+(a-1)](對判別式正負展開討論) 評注:本題討論較為繁瑣,與例2的不同地方在于本題的分子可以直接因式分解,也是高考常考題型,對于能夠因式分解的題型,直接進入第三步,先判斷根是否在定義域內,再對兩根大小展開討論即可,無需再考慮判別式的正負.如果不按照分類討論的標準進行極易出現錯誤. 通過上面的幾個典型例題我們發現,對于求導后是一元一次不等式型,分類討論標準為:第一步若一次項系數含參,需要對一次項系數的正負展開討論;第二步求出對應方程的根后判斷根是否在定義域內展開討論. 求導后為一元二次不等式型,分類討論的標準為: 第一步:看二次項系數是否含參,若含參,需要對系數分大于零、等于零和小于零分別展開討論.若二次項系數為零,按照一元一次不等式題型解決;當二次項系數大于零(或小于零)進入第二步; 第二步:求出對應一元二次方程的判別式,分Δ≤0(函數在定義域上恒增或恒減)和Δ>0展開討論.若Δ>0則進入第三步; 第三步:當Δ>0時,求出對應方程的兩個不等實根. ①判斷兩個實根是否在定義域內,如果不能直接判斷,需要展開討論.其中兩個實根都不在定義域內或者只有一個實根在定義域內可直接解二次不等式(或借助二次函數圖像).若兩個實根都在定義域內,則需要進入下一步. ②判斷兩根大小關系,若無法確定大小,則需要對兩根的大小展開討論. 最后,提供幾道試題供參考: 1.(2019年長沙市第五次調研文科第21題節選)已知函數f(x)=lnx+ax2,其中a∈R,討論函數f(x)的單調性. 3.(2017年天津文科數學第21題節選)已知函數f(x)=x3-6x2-3a(a-4)x+b,其中a,b∈R,|a|<1,討論函數f(x)的單調性. 4.(2016年四川高考文科數學第21題節選)設函數f(x)=ax2-a-lnx,其中a∈R,討論函數f(x)的單調性.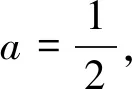
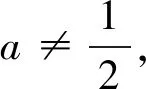
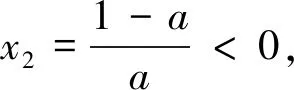
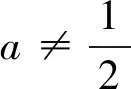

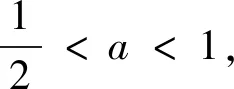
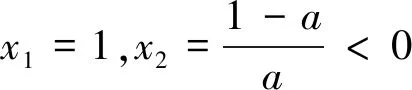
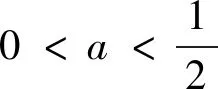
三、總結反思