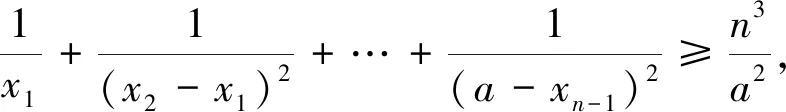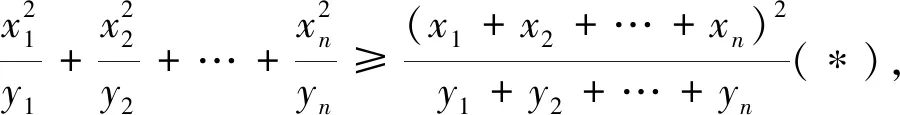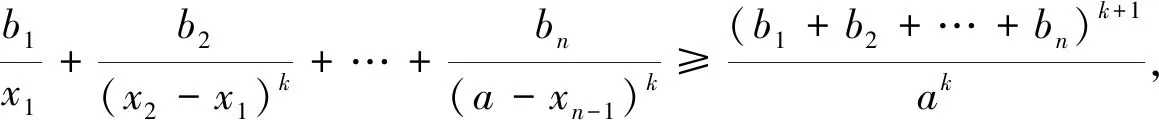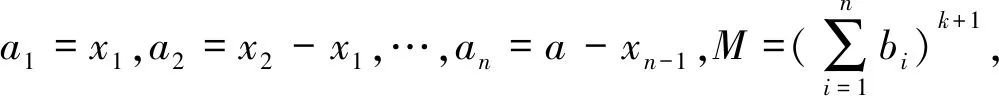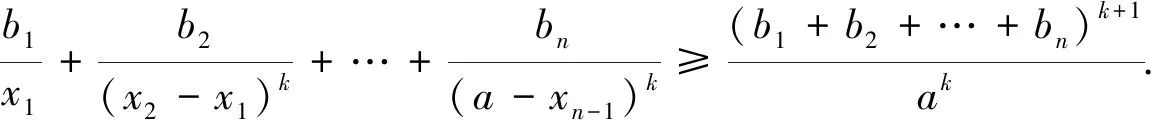一道競賽填空題的一題多解與拓展

新疆實驗中學 (830049) 晏 鴻

高中數學教學內容多，學生天天在做題，老師天天在講題，好像數學題永遠做不完，那么有沒有一種行之有效的學習方法？如果現在還沒有，不妨嘗試一下一題多解.可能有人會認為，追求一題多解，會加重負擔.本人認為不盡然，因為一題多解是用多種方法解決同一道問題，在解決問題的同時復習鞏固多項數學基礎知識，熟練多項解題技能，積累各種解題經驗.實際上就是跳出題海，通過有限的訓練達到掌握多種方法的目的.本文以一道新疆初賽填空題為例說明.

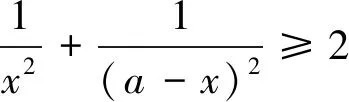
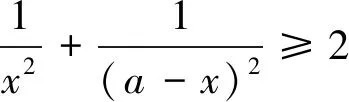
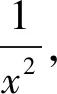
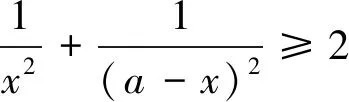
思路2：在考慮選用代數方法解決問題時，三角代換也是常用的方法，直接代換不行，但觀察不等式發現分母有x,a-x，就可以考慮給它倒過來相加，再除以a就可以得到常數1，順利引進正余弦平方和公式，把整個問題轉化為三角方面的運算，這種想法的關鍵在于要有轉化思想.

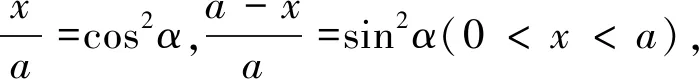
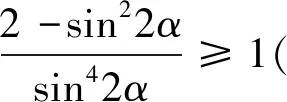
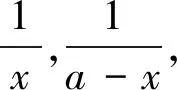
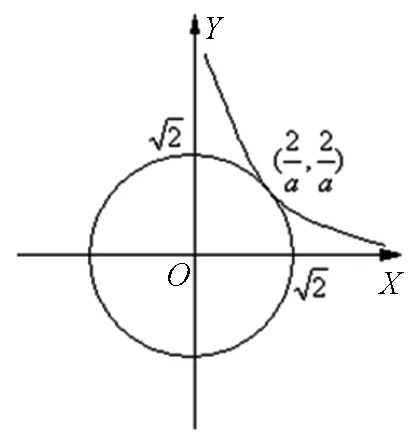
圖1

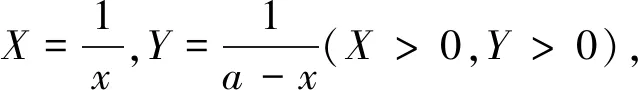
思路4：前面的幾種想法本質都是在轉化，那能不能直接用不等式解決這個問題?由于是競賽題，可以考慮選用常規的結論“平方平均值大于等于調和平均值”來入手.

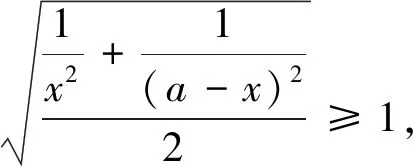
評注:以上四種解法，基本上選用的是解決高考題的常規方法，在日常的學習過程中，需要學生夯實基礎，熟練技巧，理解方法的本質、功能，增強解題思維能力，培養學習數學的興趣，提高學習實效性.

思路5：一般情況下，競賽題用解決高考題的常規方法去做會比較麻煩，但如果選用解決競賽題的非常規思路去想，用均值不等式，柯西不等式以及柯西不等式的變形來做，就方便多了.

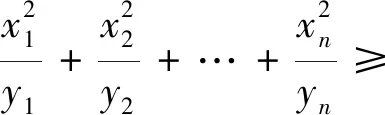
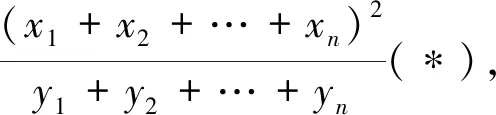
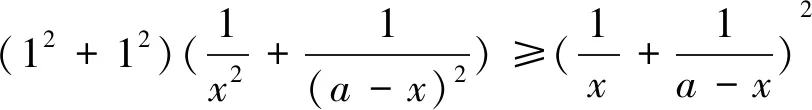
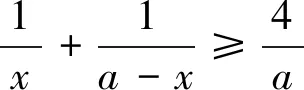
思路6：把解法5的不等式(*)進行變形，把分子處理掉，變成更簡潔的形式，與題目條件直接對接，立馬解決問題.只要繼續往下做，就可以發現這種想法是可行的.

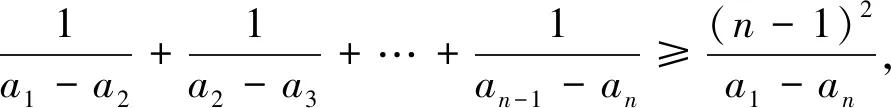
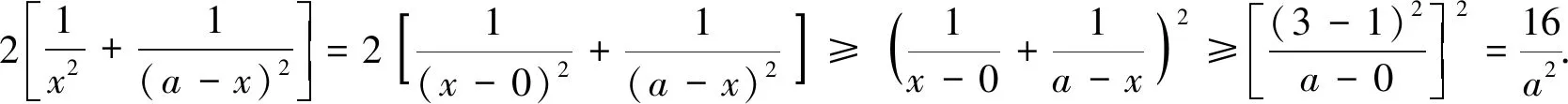
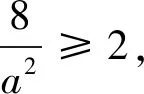
評注:后兩種解法，選用的是非常規方法，優點是解題速度快，缺點是需要記住的中間結論多，很難想到,因此在平常的學習過程中，不要過分強調哪一種方法的重要性，而是要理解題意，分析條件，因題施策，出奇制勝，提高練習的實戰性.六種解法各有特點，都值得仔細研究.

此題可作如下推廣：

推廣1 若0

總之，本題在具體的課堂教學過程中，學生們反應熱烈，課堂氣氛活躍，大多數同學都能提出自己的想法，因此老師有意識，有目的的進行了引導，誘發學生的內在動力，激發他們的探索求知欲望，使他們精神飽滿，心情舒暢地漸入“解題境界”.仁者見仁，智者見智.一題多解主要是讓學生學會從不同角度、不同側面去思考問題,培養良好的思維品質,拓展解題空間，是讓學生跳出題海的一件法寶.