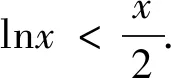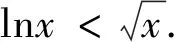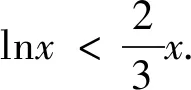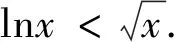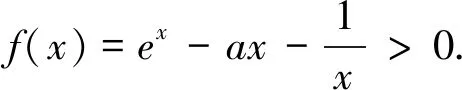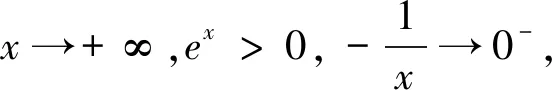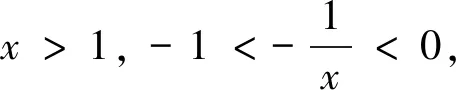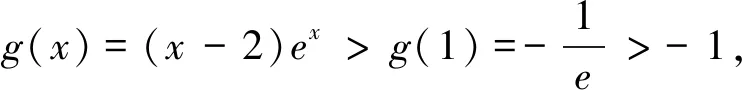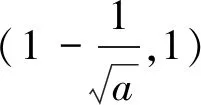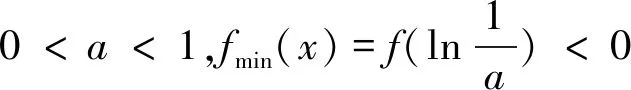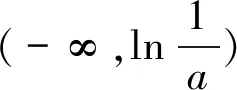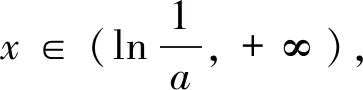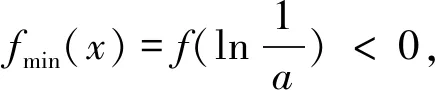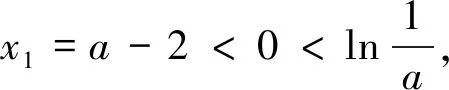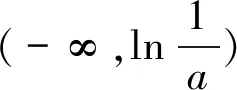放縮法求函數的零點 *

福建省泉州市第七中學 (362000) 黃永生 紀建靈 楊 丹

縱觀2015年至2018年全國Ⅰ卷解答題導數部分試題，函數的零點問題一直倍受命題人青睞.為嚴謹地運用零點存在性定理，標準答案經常會出現匪夷所思的取點.本文嘗試從放縮法的尺度和方法入手，呈現標準答案中未呈現的取點過程，并形成可操作的有效方法，希望對讀者有所幫助.限于篇幅，本文僅關注試題的取點部分.

1.放縮法

要尋找f(x)<0的一個解，需將f(x)放大到g(x)，只要能找到g(x)<0的一個解即可；同理，要尋找f(x)>0的一個解，只需將f(x)縮小到g(x)，找到g(x)>0的一個解即可.

2.放縮原理

(1)存在x0∈R+,使得當x>x0，有lnx0);

(2)存在x0∈R+,使得當0-xα(α<0);

(3)存在x0∈R-,使得當x

注：上式中的α均可根據需要取值.

3.放縮法的尺度問題

例1若函數f(x)=lnx-x-a有兩個不同的零點，求實數a的取值范圍.

解：依題意，易知f(x)在(0,1)單調遞增，在(1,+∞)單調遞減.即fmax(x)=f(1)=-1-a.

若函數f(x)有兩個零點，當且僅當下列三個條件同時成立:

①f(1)=-1-a>0.②?x1∈(0,1),使得f(x1)<0.③?x2∈(1,+∞),使得f(x2)<0.

這里僅以條件③為例討論放縮法的尺度問題.

放縮一：由于x∈(1,+∞)時，根據放縮原理(1)得lnx<2x.所以f(x)=lnx-x-a<2x-x-a=x-a.令g(x)=x-a<0，得x

兩種放縮都是將lnx進行放大，但是得到的結論相去甚遠，原因在哪？仔細分析，當x→+∞時，函數f(x)<0，g(x)>0，h(x)<0.放縮一得到函數g(x)改變了原有函數f(x)的變化趨勢！據此，可以得到以下關于放縮法尺度問題的一個結論：不論是將函數f(x)放大(縮小)，應當保證放大(縮小)得到的函數g(x)在自變量x趨向于定義域某端點時，具有與函數f(x)相同的變化趨勢.所以，在將函數f(x)放縮之前，應當運用極限，判斷函數f(x)中各項的正負，并把握好函數f(x)的整體變化趨勢.同時也可以明確要取的點的區間的大致范圍.基于此，例1條件③還可以有其它取點方法，例如：

4.放縮法的幾種技巧

(1)利用代數式的正負性，舍項放縮

例2 當a>0時，請取一個數x∈(0,+∞)，使f(x)=ex+x2-ax>0.

分析：當x→+∞,ex>0,x2>0，要將函數f(x)縮小，可將正數項舍去.

解：當x→+∞,ex>0,x2>0，所以f(x)=ex+x2-ax>x2-ax，令x2-ax≥0，得x≥a.取x0=a，則f(x0)=f(a)=ea+a2-a2=ea>0.

評析：本例中ex>0,x2>0，要取一個數使f(x)>0，舍去ex,x2中哪一項都可以，只是保留x2得到的不等式更容易解.但是不能將ex,x2同時舍去，否則得到-ax就是一個負數，本質上改變了函數f(x)在x→+∞時的變化趨勢.

(2)利用放縮原理，調整放縮

例3 已知a<-1，取一個數x∈(1,+∞)，使得f(x)=alnx+x-a2>0.

分析：當x→+∞,x>0,alnx<0，要將函數f(x)縮小，不能簡單將alnx舍去.由于x→+∞時，f(x)→+∞，可將alnx縮小.

評析：本例中為了將參數a消去，可取x0=ea，但此時x0=ea?(1,+∞).當函數f(x)均存在正負項時，應當在保證函數f(x)整體變化趨勢不變的前提下，根據放縮原理進行局部的調整放縮.

(3)利用局部限制，放縮無窮小量

5.高考試題應用舉例

例5(2016全國Ⅰ卷理21)函數f(x)=(x-2)ex+a(x-1)2，試說明已知a>0，fmin(x)=f(1)<0時，f(x)有兩個零點.

分析：當x→-∞，(x-2)ex為反向無窮小量，考慮局部限制放縮；當x→+∞時，(x-2)ex>0，

a(x-1)2>0，考慮舍項放縮.

解：易知a>0時，f(x)在(-∞,1)單調遞減，在(1,+∞)單調遞增.

令(x-2)ex≥0，解得x≥2.取x0=2，則f(2)=a>0.

分析：當x→+∞時，ae2x>0，(a-2)ex<0，-x<0，考慮根據放縮原理調整放縮；當x→-∞，(a-2)ex為反向無窮小量，考慮局部限制放縮，ae2x>0，考慮舍項放縮.

當x∈(-∞,0)時，0(a-2)ex-x=(a-2)-x.