完全正則半群的可裂子半群

余保民,朱天民

(渭南師范學院 數理學院，陜西 渭南 714099)

完全正則半群是一類重要的正則半群并得到廣泛的應用和研究[1-4]。可裂半群是一類具有特殊結構的完全正則半群，最早由Rédei在研究半群的Frattini結構時引入[5]。Tamura等[6]從冪半群的角度對這類半群進行了研究；Giraldes等[7]從半群的生成元出發研究了這類半群的性質和結構。近年來，趙憲鐘、甘愛萍等[8-11]把可裂半群應用于冪半群和半群類整體決定性問題的研究上，通過研究Clifford半群、帶和正規純整群的可裂子半群的性質，解決了這些半群類的整體決定性問題。因此，本文將研究完全正則半群的可裂子半群的性質，給出這一類子半群的刻畫，相信對完全正則半群的可裂子半群的研究，將對分析完全正則半群冪半群的性質以及解決完全正則半群類的整體決定性起重要作用。

對于文中未加定義的概念和術語，可參見文獻[1-2]。

1 預備知識和基本概念

定義1[2]設S為一半群，如果對S中的任一元素a，都存在x∈S，使得axa=a且ax=xa，則稱S為完全正則半群。

熟知，完全正則半群S的H-類都是群，因此，完全正則半群是群并半群[1-2]；S上的J-關系是一個半格同余，且每一個J-類都是完全單半群。有如下關于完全正則半群的結構定理，見文獻[1]中定理4.1.3和文獻[2]中定理Ⅱ.1.4。

Clifford定理完全正則半群是完全單半群的半格。

本文中，如無特別說明，總是假設S是完全正則半群，且S=[Y;Sα]是完全單半群Sα的半格Y，這里Y?S/J，Sα是S的J-類。對a∈S，分別用Ha、La和Ra表示a所在的H-類、L-類和R-類；a-1表示a在Ha中的逆元；用a0表示Ha的單位元。易知，aHb?a0=b0，同時，用P(S)表示S的非空子集的全體，并在P(S)上定義乘法如下：

AB={ab|a∈A,b∈B}

則P(S)成為一個半群，稱為S的冪半群。用EP(S)表示P(S)中冪等元全體之集，即

EP(S)={X∈P(S)|X2=X}

設A∈P(S)，令Aα=A∩Sα，

Id(A)={α∈Y|Aα≠?}

容易證明，

Id(AB)=Id(A)Id(B)

(1)

定義2[5]如果半群S的任一非空子集都是S的子半群，則稱S是可裂半群。

根據文獻[5]中定理50和文獻[6]的定理5.4，有如下關于可裂半群的刻畫。

引理1設S是一個半群，則以下說法等價：

1)S是可裂半群；

2)?X∈P(S),X2=X。

3)?a,b∈S,ab∈{a,b}。

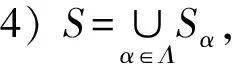
Pelikán[12]把可裂半群的概念進行了推廣，引入并研究了滿足條件

(An):(?a1,a2,…,an∈S)a1a2…an∈{a1,…,an}

的半群。由引理1易知，S是可裂半群當且僅當S滿足條件(A2)，并且容易看到可裂半群滿足條件(An)，其中n≥2。Pelikán證明了如果存在正整數k，使半群S滿足條件(A2k)，則S為可裂半群；若S滿足條件(A2k+1)，其中k≥2，則S滿足條件(A3)，根據文獻[12]的定理2和文獻[13]的定理1，有如下結果：

引理2設S是一個半群，則以下說法等價：

1)S滿足條件(A3)。

2)?X∈P(S)，X3=X。

3)P(S)是正則半群。

以下分別用A2(S)和A3(S)來表示完全正則半群S的滿足條件(A2)和滿足條件(A3)的子半群之集，顯然有

A2(S)?A3(S)?EP(S)

以下將研究完全正則半群S的可裂子半群的性質，并給出其刻畫。

2 主要結果

為給出完全正則半群S的可裂子半群的刻畫，首先研究滿足條件(A3)的子半群的性質。

容易證明下面的結果。

引理3設M∈A3(S)，X?M,若X2=M，則X=M。

引理4設M,X∈P(S)，若X2=M，則Id(X)?Id(M)。特別地，若Id(M)是Y的子鏈，則Id(X)=Id(M)。

證明由X2=M及式(1)可知，?α∈Id(X)，

α=α2∈(Id(X))2=Id(X2)=Id(M)

因此Id(X)?Id(M)。若Id(M)是Y的子鏈，則Id(X)是Id(M)的子鏈，從而

Id(X)=(Id(X))2=Id(X2)=Id(M)

下面的命題是文獻[10]的引理2.5和文獻[11] 的引理2.3.4的推廣。

命題1設M∈EP(S)。若?X∈P(S)，

X2=XM=MX=M

則以下結果成立：

1)?a∈M,a3=a且a0∈M。

2)?a,b∈M，ab∈{a,b,a0,b0}。

3)Id(M)是Y的子鏈。

4)若存在a∈M使得a2≠a，則Ha∩M={a,a0}。

5)?α∈Id(M)，Mα包含于Sα的一個L-類或R-類中。

6)?α∈Id(M)，若α不是Id(M)的最大元，則Mα是左零半群或右零半群；當β∈Id(M)且α<β，a∈Mα，b∈Mβ時，ab=ba=a。

7)若Id(M)有最大元ω且存在a∈Mω使得a2≠a，則Mω={a,a0}為2階循環群。

證明設M∈EP(S)滿足條件：?X∈P(S)，當X2=XM=M時有X=M。

1)若存在a∈M使得a3≠a，則a≠a2且a3≠a2。實際上，若a2=a3，則a=a-1a2=a-1a3=a2，從而a=a2=a3，矛盾。故a3≠a2。令X=M{a3},由文獻[10]中引理2.5的證明可知X2=M，又因X?M，所以M=X2?XM?M2=M，故X2=XM=M。易見X≠M，與假設矛盾，因此?a∈M，a3=a，這時a0=a2∈M2=M。

2)假設存在a,b∈M使得ab?{a,b,a0,b0}。令X=M{ab}，則a,b,a0,b0∈X，因X?M，故X2?M2=M；反之，有M?X2。實際上，?s∈M，若s∈X且s0∈X，則s=ss0∈X2；若s∈X，s0?X，則s0=ab=abb0=s0b0，從而s=ss0=ss0b0=sb0∈X2；若s?X，則s=ab∈X2。綜上，有?s∈M，s∈X2，即M?X2。因此，M=X2，又因X?M，所以M=X2?XM?M2=M，故X2=XM=M。由于X≠M，與假設矛盾，所以?a,b∈M，ab∈{a,b,a0,b0}。

3)是2)的直接推論。

4)設a∈M使得a2≠a，則由命題1的1)可知，a2=a0∈M，所以a-1=a.若b∈Ha∩M，則a0=b0。由命題1的2)可知，ab∈{a,b,a0}，若ab=a，則

b=a0b=a-1(ab)=a(ab)=a2=a0∈M

若ab=b，則a=ab0=(ab)b-1=bb-1=b0=a0，矛盾，故ab≠b；若ab=a0，則

b=a0b=a-1(ab)=a(ab)=aa0=a∈M

綜上，當b∈Ha∩M時有b∈{a,a0}，故Ha∩M={a,a0}。

5)設存在α∈Id(M)使得Mα不包含于Sα的任一L-類或R-類中，則存在a,b∈Mα使得b?La且a?Rb，因此可得Ha,Hb,Ra∩Lb互不相交。因Sα為完全單半群，故ab∈Ra∩Lb。由于{a,a0,b,b0}?Ha∪Hb，但

(Ha∪Hb)∩(Ra∩Lb)=?

從而ab?{a,b,a0,b0}，與命題1的2)矛盾。因此，?α∈Id(M)，Mα包含于Sα的一個L-類或R-類中。

6)設α,β∈Id(M)且α<β，a∈Mα。由命題1的2)可知a2=a或a0。若a2=a，則a=a2=a0；若a2=a0≠a，則令X=M{a0}，由文獻[10]中引理2.5的證明可知X2=M。類似于1)和2)的證明，可知X2=XM=M，但X≠M，與假設矛盾，故Mα中的元素都為冪等元。進一步，由命題1的5)可知，Mα為左零半群或右零半群。現設a∈Mα，b∈Mβ，則ab∈Sα，b,b0∈Sβ。由2)知ab∈{a,b,b0}，從而ab∈Sα∩{a,b,b0}={a}，故ab=a，對偶地可證明ba=a。

下面給出滿足條件(A3)的子半群的刻畫。

定理1設S是完全正則半群，M∈EP(S)，則M∈A3(S)當且僅當?X∈P(S)，

X2=XM=MX=M

證明()設M∈A3(S)且X2=XM=M，因M∈A3(S)，由引理2可知Id(M)是一個鏈，又因X2=M，由引理4可知Id(X)=Id(M)。現設a∈X，則a2∈X2=M，從而a0=(a2)0∈M。由XM=M可知，a=aa0∈XM=M，因而X?M。由引理3可得X=M。

(?)如果M∈EP(S)滿足條件?X∈P(S)，

X2=XM=MX=M

則由命題1和引理2可知M∈A3(S)。

對偶地，可以證明M∈A3(S)，當且僅當

?X∈P(S),X2=MX=MX=M

引理6(見文獻[2]的Proposition III.1.1]) 設S是完全正則半群，則S是完全單半群當且僅當S滿足等式a=(ax)0a。

下面給出S的可裂子半群的刻畫。

定理2設M∈A3(S)，則M∈A2(S)當且僅當?X∈P(S)，

[Id(X)?Id(M),XM=MX=M]X2=X

證明設M∈A3(S)，首先證明?X∈P(S)，當Id(X)?Id(M)且XM=MX=M時有X?M。設α∈Id(X)，a∈Xα，b∈Mα，則ab∈XM=M，從而由命題1可知(ab)0∈M，因Sα為完全單半群，由引理6可知a=(ab)0a∈MX=M，所以X?M。

(?)如果M∈A3(S)A2(S)，則由引理2可知Id(M)有極大元ω，且Mω={a,a0}為2階循環群。令X={a}，易知Id(X)?Id(M)，XM=MX=M，但X2={a0}≠{a}=X，所以當M∈A3(S)滿足條件?X∈P(S)，[Id(X)?Id(M),XM=MX=M]X2=X時，一定有M∈A2(S)。