新課標下高中數學教材例題設置的難度研究
劉佳 李琪 蘇淑華 皮帥玲

摘 要 數學教材是將教育理念、課程標準轉化為實際教學的主要載體,而教材中的例題是把數學知識、技能、思想和方法聯系起來的紐帶。以北師大版平面向量的例題為例分析高中數學難度情況。研究發現,北師大版平面向量的例題設置在計算和推理水平難度較大,在背景和認知水平難度較低,同時也體現了對數學學科核心素養的考查。
關鍵詞 課程標準 高中數學教材 例題 青浦模型
中圖分類號:G424?????????????????????????????????????文獻標識碼:A ???DOI:10.16400/j.cnki.kjdkz.2019.07.065
A?Study?on?the?Difficulty?of?Setting?Examples?in?Senior?Mathematics
Textbooks?under?the?New?Curriculum?Standard
——Take?plane?vector?as?an?example
LIU?Jia,?LI?Qi,?SU?Shuhua,?PI?Shuailing
(Fuzhou?Normal?College?of?ECUT,?Fuzhou,?Jiangxi?344000)
Abstract Mathematics?textbooks?are?the?main?carriers?of?transforming?educational?concepts?and?curriculum?standards?into?practical?teaching.?Examples?in?the?textbooks?are?the?links?between?mathematical?knowledge,?skills,?ideas?and?methods.?Taking?the?example?of?plane?vectors?in?the?edition?of?Beijing?Normal?University?as?an?example,?this?paper?analyses?the?difficulty?of?high?school?mathematics.?It?is?found?that?the?example?setting?of?plane?vectors?in?the?edition?of?Beijing?Normal?University?is?more?difficult?in?calculation?and?reasoning,?less?difficult?in?background?and?cognitive?level,?and?also?reflects?the?examination?of?the?core?literacy?of?mathematics.
Keywords curriculum?standard;?senior?mathematics?textbooks;?examples;?Qingpu?Model
1?研究背景
2018年1月正式頒布了新修訂的《普通高中數學課程標準(2017年版)》,新課標明確提出育人的核心目標就是培養學科素養。數學學科素養包括:數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析。這些數學學科核心素養即相對獨立,又相互交融,是一個有機的整體。數學核心素養可以通過四個方面得以體現,包括:情境與問題、知識與技能、思維與表達和交流與反思。
如何對教材進行定量和定性研究,以期更好的服務師生,成為許多學者的研究目標,而數學例題又是有效教學的關鍵,以往的研究更多的是對教材的比較研究,而且大多是對習題的難度研究,對例題的研究相對較少。例如史寧中等建立課程難度模型,鮑建生利用綜合難度模型對教材習題難度進行了研究,來考察不同版本的難度情況。[1]
例題教學是數學教學的重要組成部分,是抽象的概念、定理、公式和具體實踐之間的橋梁,是使學生的數學知識轉化為數學能力,形成數學核心素養的重要環節,近年來隨著數學課程改革的不斷推進,在例題設置上也需要開始轉變,在這樣的背景下,以北師大版平面向量的例題為例,通過用青浦模型對高中數學例題的綜合難度分析,探究例題對數學科學素養的考察情況。
2?例題難度分析
就目前教材研究分析而言,青浦模型還是一個相對比較客觀,操作性強,可量化,能夠反映教材難度水平的一個測量工具,而且還能體現完整的數學活動過程。通過青浦模型對例題的難度分析,可以體現情境與問題、知識與技能、思維與表達和交流與反思四個方面考察的水平層次,進而體現數學學科核心素養考察情況。
2.1?背景維度分析
數學問題的“背景”因素劃分為四個不同的層次水平:無背景、個人生活、公共常識和科學情境。在北師大版平面向量例題中,每道題都有其相應的背景,以例題2為例。[2](P75,例2)
難度分析:該題從生活實際問題出發,考察了平面向量的知識,需要學生掌握一定的預備知識,具有一定的數學抽象的能力。解答該題首先將船港問題抽象成平面向,根據向量的關系得到。該題背景水平為2,認知水平為3,計算水平為4,推理水平為2,知識水平為3。這個例題其實是以輪船行駛問題為背景,要求學生在真實情境中將具體問題抽象成數學問題,即體現數學抽象素養的內涵,同時對數學建模、數學運算作出相應的要求。
2.2?認知水平
認知水平可以分為四個層次:計算、概念、領會和分析。教材中的例題在不同層次考察認知水平,以例題2為例[2](P83,例2)
難度分析:該例題從圖像出發,考察平面向量共線性質的判定依據需要學生對向量共線概念,向量的幾何運算知識的掌握,運用數形結合的思想解決數學問題,具有一定的數學直觀想象素養。從題中得到。該題的背景水平為1,認知水平為1,計算水平3,推理水平為2,知識水平為1。這道平面向量共線判定問題,要求學生能在認知水平上領會概念、性質的內涵并能靈活運用,同時也考察數學直觀想象素養。
2.3?運算
根據鮑建生的青浦模型,數學題里的運算水平可以分為以下四個層次:無運算、數值計算、簡單的符號運算和復雜符號運算。以例題5為例[2](P84,例題5)
難度分析:本題從圖形出發,考察平面向量加減運算。根據向量的幾何意義,得到:。該題的背景水平為1,認知水平為1,計算水平為3,推理水平為2,知識水平為2。該題需要學生掌握平面向量的幾何意義和線性運算,靈活運用平面向量的運算,具有一定的數學運算素養。
2.4?推理
根據鮑建生的綜合難度青浦模型,推理維度可分為三個水平層次:無推理、簡單推理和復雜推理。推理的一般形式為:“因為…所以…”以例題3為例[2](P94,例題3)
難度分析:該題從菱形對角線垂直證明出發,考察平面向量垂直性質,則向量相乘為0的知識點。解答該題需要證明:。該題的背景水平為1,認知水平為4,計算水平為3,推理水平為2,知識點水平為3。該題需要學生用逆向思維從結果反推條件,學會用向量去解決幾何問題,對平面向量的乘法運算熟練運用,需要具有一定的邏輯推理素養。
2.5?知識含量
知識含量就是一道例題中所含知識點的個數,知識含量分為三個水平層次:一個知識點、兩個知識點和三個或三個以上知識點。以例題5為例[2](P78,例題5)
難度分析:本題從數學計算出發,考察向量的模的概念和計算。解答該題的關鍵是:即。該題的背景水平為1,認知水平為3,計算水平為4,推理水平為2,知識水平為3。該題需要學生掌握向量模的概念和計算,即其幾何意義,運用數形結合的思想,對問題進行深度解析、判斷、計算,具有一定的數學邏輯推理和直觀想象素養。
3?綜合難度匯總分析
為了了解高中數學例題設置難度情況,對北師大版平面向量共31道例題5個維度進行詳細的分析,根據因素水平權重,利用以下公式可以計算例題在每個因素的加權平均值:
其中,d_{i}表示第i個難度因素上的加權平均值,d_{ij}表示第i個難度因素的第j個水平的權重,這里直接采用等級權重,即d_{ij}=j;n_{ij}則表示這套教科書例題中屬于第i個難度因素的第j個水平的題目的個數,則n是樣本總數。顯然,對如何i,都有。
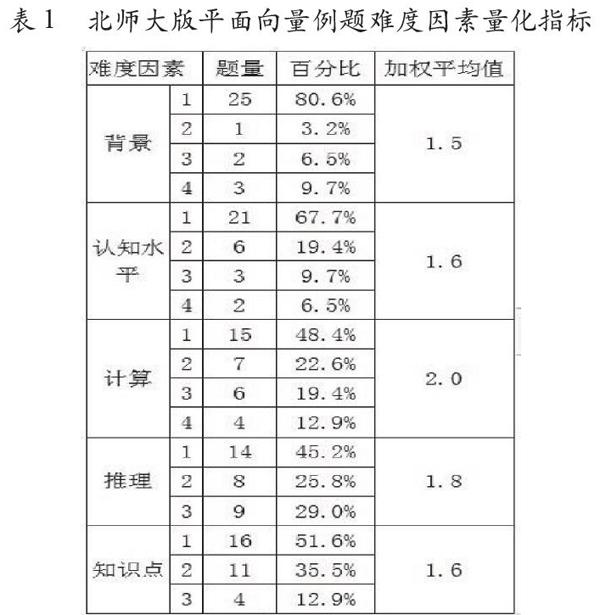
匯總如表1。通過分析表1中的數據可以發現,例題在不同維度不同水平均有設置,能夠體現數學學習的活動過程,間接體現數學學科核心素養。例題在每個維度的低水平所占比例高達一半以上,特別是背景維度和認知水平,分別高達80.6%和67.7%;而且各個維度的加權平均值存在差異,其中計算和推理維度的加權平均值較大,分別為2.0和1.8,明顯高于其他維度,而背景和認知水平的加權平均值較低,說明我們現有的北師大版教材比較注重數學計算和推理,偏向對基本知識和技能的學習和培養,但對背景和認知水平設置偏少,對基本經驗和基本過程設計甚少。通過第二節的難度因素分析,不難發現,有些例題在各維度都在一個比較高的水平,綜合體現了數學學科核心素養,如北師大版平面向量例題3、4、5、30、31等。
4?結論與建議
通過對北師大版高中數學教材“平面向量”例題的難度分析,結合數學核心素養的考察,研究發現:現有北師大版高中數學平面向量例題設置比較全面,不僅考察了學生的基本知識和基本技能,也考察了學生的基本思想和基本經驗。例題以學科知識為載體,以數學能力為核心,對各維度進行了考察,但是目前的例題整體設置偏向對數學計算和推理的考察,而對背景和認知水平的考察較少。
數學例題作為數學教學過程中的關鍵一環,肩負著服務師生、提高教學效率的重要使命,對新課標的目標實現發揮著至關重要的作用,為了改善高中數學例題設置情況,基于上述分析提出建議:對于高中數學新課標的育人目標要求以數學學科核心素養為導向,教材例題的設置要以學生的認知水平為基礎,發展學生數學學科核心素養為宗旨。隨著時代的迅猛發展,新興技術也在高速發展,為了更好的?適應未來的工作與生活,高中學生需要具備數學建模與數學探究能力,建議在例題設置背景更加情境化,例題的開放性可以有所增強,把數學學科核心素養融入到具體的知識內容和思想方法中。
參考文獻
[1] 張盧西子.中法兩國高中數學教材例題的綜合難度比較[D].華東師范大學,2017:11-12.
[2] 普通高中課程標準實驗教科書?數學必修4.北京師范大學出版社:69-102.

