高等數(shù)學(xué)教學(xué)中融入思想政治教育芻探
周曉燕


摘 要:學(xué)生的全面發(fā)展是教育教學(xué)的最終目標(biāo),教師應(yīng)該把思想政治教育融入到教育教學(xué)活動(dòng)中。文章探討高職院校數(shù)學(xué)教師在高等數(shù)學(xué)教學(xué)過(guò)程中如何有效融入思想政治教育,并對(duì)學(xué)生加強(qiáng)理想信念教育、集體主義教育、誠(chéng)信教育、人文教育等,以促進(jìn)學(xué)生全面發(fā)展,培養(yǎng)學(xué)生合作精神、誠(chéng)實(shí)守信等優(yōu)良品質(zhì)。
關(guān)鍵詞:高等數(shù)學(xué);思想政治教育;教學(xué)方法;誠(chéng)實(shí)守信;全面發(fā)展
中圖分類(lèi)號(hào):G641;G712 文獻(xiàn)標(biāo)志碼:A 文章編號(hào):1008-3561(2019)27-0007-02
一、背景
中共中央、國(guó)務(wù)院發(fā)布的《關(guān)于進(jìn)一步加強(qiáng)和改進(jìn)大學(xué)生思想政治教育的意見(jiàn)》特別強(qiáng)調(diào)“充分發(fā)揮課堂教學(xué)在大學(xué)生思想政治教育中的主導(dǎo)作用”。思想政治教育從來(lái)都不是完全獨(dú)立于其他學(xué)科而存在的,高校中的每門(mén)課程都具有很強(qiáng)的育人功能,每位教師都肩負(fù)著教書(shū)育人的職責(zé)。
“高等數(shù)學(xué)”是大學(xué)生的一門(mén)基礎(chǔ)必修課程,在高等學(xué)校教育中有著舉足輕重的地位。為此,筆者按照高職教育的人才培養(yǎng)模式及“高等數(shù)學(xué)”這門(mén)學(xué)科的要求,結(jié)合本校的實(shí)際情況,通過(guò)調(diào)查問(wèn)卷進(jìn)行統(tǒng)計(jì)分析,并通過(guò)開(kāi)展師生座談會(huì)和教學(xué)實(shí)踐嘗試等,研究如何更好地在高職高等數(shù)學(xué)教學(xué)中加強(qiáng)大學(xué)生的思想政治教育,把育人工作有效滲透到課堂教學(xué)中。
二、研究過(guò)程
面向全院開(kāi)設(shè)“高等數(shù)學(xué)”“計(jì)算機(jī)數(shù)學(xué)”“經(jīng)濟(jì)數(shù)學(xué)”等數(shù)學(xué)類(lèi)課程的全體學(xué)生開(kāi)展問(wèn)卷調(diào)查。問(wèn)卷調(diào)查的結(jié)果顯示:81.5%的學(xué)生希望教師在上數(shù)學(xué)課的時(shí)候介紹數(shù)學(xué)發(fā)展史;78.2%的學(xué)生覺(jué)得學(xué)習(xí)數(shù)學(xué)可以鍛煉他們的創(chuàng)新能力;89.1%的學(xué)生認(rèn)為我國(guó)古代的數(shù)學(xué)家取得了超前于世界其他國(guó)家的先進(jìn)成果;91%的學(xué)生喜歡教師利用先進(jìn)的教學(xué)資源及手段開(kāi)展課堂教學(xué);83%的學(xué)生希望教師可以在課堂上開(kāi)展形式多樣的教學(xué)活動(dòng),如分組討論、搶答等;98.2%的學(xué)生認(rèn)為數(shù)學(xué)教師和學(xué)校的思想政治輔導(dǎo)員及“兩課”教師一樣,將影響著他們思想道德的培養(yǎng)與成長(zhǎng);83%的學(xué)生認(rèn)為數(shù)學(xué)學(xué)科的特性,有利于培養(yǎng)他們的抽象思維和縝密概括的能力。
通過(guò)認(rèn)真分析問(wèn)卷調(diào)查結(jié)果,并結(jié)合師生座談會(huì)及教學(xué)實(shí)踐嘗試等,筆者認(rèn)為,在高職高等數(shù)學(xué)教學(xué)中融入思想政治教育,可以從以下幾個(gè)方面進(jìn)行。(1)在日常的課堂上,教師講授數(shù)學(xué)知識(shí)時(shí)要積極引導(dǎo)學(xué)生,進(jìn)行理想信念教育、人文教育,積極引導(dǎo)學(xué)生進(jìn)行思維創(chuàng)新。數(shù)學(xué)知識(shí)中的性質(zhì)、公理、定理、公式等都是前人及數(shù)學(xué)家們?cè)诳陀^世界、現(xiàn)實(shí)生活中經(jīng)過(guò)種種努力,克服各種困難才抽象概括出來(lái)的。教師要通過(guò)介紹數(shù)學(xué)家們積極探求真理的事跡,讓學(xué)生學(xué)習(xí)科學(xué)家們不畏艱難、勇于求知的精神。教師還要深入探索,發(fā)掘數(shù)學(xué)文化中的人文價(jià)值,進(jìn)而活躍課堂氛圍,提高學(xué)生學(xué)習(xí)的積極性。(2)教師在教學(xué)中可以采用分組討論、代表總結(jié)等方法對(duì)學(xué)生進(jìn)行集體主義教育,讓學(xué)生分工合作,共同達(dá)成學(xué)習(xí)目標(biāo)。教師要通過(guò)讓學(xué)生自己思考、小組討論的形式,提高語(yǔ)言交流的能力。教師要結(jié)合學(xué)生熟悉的生活事例,讓學(xué)生與教師及同學(xué)共同合作,培養(yǎng)他們主動(dòng)學(xué)習(xí)的能力。(3)教師在數(shù)學(xué)教學(xué)過(guò)程中要加強(qiáng)誠(chéng)信教育。數(shù)學(xué)是一門(mén)嚴(yán)謹(jǐn)?shù)膶W(xué)科,教師向?qū)W生教授的各種運(yùn)算性質(zhì)、各類(lèi)公式以及定理等都具有很強(qiáng)的邏輯性。因此,教師要把思想政治教育潛移默化地融入數(shù)學(xué)教學(xué)中,培養(yǎng)學(xué)生嚴(yán)謹(jǐn)?shù)倪壿嬎季S能力,培養(yǎng)學(xué)生實(shí)事求是的科學(xué)態(tài)度,進(jìn)而使學(xué)生形成積極正確的世界觀、人生觀和價(jià)值觀。(4)教師在數(shù)學(xué)教學(xué)中要引經(jīng)據(jù)典(古代數(shù)學(xué)家的成就),激發(fā)學(xué)生的愛(ài)國(guó)情感。在數(shù)學(xué)教學(xué)中,教師可將我國(guó)的數(shù)學(xué)史融入課堂教學(xué),介紹相關(guān)的古代數(shù)學(xué)家的成果,使學(xué)生樹(shù)立文化自信,克服崇洋媚外的心理,增強(qiáng)民族自豪感,以自己身為中國(guó)人而驕傲。教師還要讓學(xué)生充分認(rèn)識(shí)到自己的社會(huì)責(zé)任,傳承祖先的文化,勇于擔(dān)當(dāng),進(jìn)而激發(fā)學(xué)生學(xué)習(xí)熱情和愛(ài)國(guó)熱情。(5)培養(yǎng)學(xué)生理論聯(lián)系實(shí)際的作風(fēng),以及數(shù)學(xué)意識(shí)和實(shí)際應(yīng)用能力。數(shù)學(xué)學(xué)科的基本特征之一是其應(yīng)用的廣泛性。隨著科學(xué)技術(shù)的飛速發(fā)展和社會(huì)的進(jìn)步,數(shù)學(xué)不但在各個(gè)傳統(tǒng)領(lǐng)域(如工程技術(shù)、經(jīng)濟(jì)建設(shè)等)發(fā)揮著越來(lái)越重要的作用,而且不斷地向新的領(lǐng)域(如生物、醫(yī)學(xué)、金融、交通、人口、地質(zhì)等)滲透。教師通過(guò)用數(shù)學(xué)知識(shí)解決學(xué)生熟知的日常社會(huì)生活中的問(wèn)題,采用學(xué)生容易理解和接受的方式傳授數(shù)學(xué)知識(shí),注重學(xué)生的親身實(shí)踐,這些都可以增強(qiáng)學(xué)生學(xué)好數(shù)學(xué)的信心。
三、教學(xué)實(shí)例
筆者現(xiàn)以“定積分的概念”課堂教學(xué)為例,簡(jiǎn)要闡述如何在日常的課堂教學(xué)中融入思政教育。
1.定積分產(chǎn)生的歷史背景——課程引入
預(yù)備知識(shí):教師要讓學(xué)生通過(guò)搶答,歸納總結(jié)常見(jiàn)的平面圖形面積的計(jì)算公式(包括矩形、菱形、平行四邊形、梯形、扇形等),調(diào)動(dòng)課堂氣氛。
案例1:《黃鶴樓送孟浩然之廣陵》(唐,李白)故人西辭黃鶴樓,煙花三月下?lián)P州。孤帆遠(yuǎn)影碧空盡,唯見(jiàn)長(zhǎng)江天際流。
分析:教師通過(guò)介紹這首名詩(shī),使學(xué)生意識(shí)到數(shù)學(xué)思想無(wú)處不在。在這首詩(shī)中,隨著帆船漸行漸遠(yuǎn),帆船的影像越來(lái)越小,最終會(huì)無(wú)限趨近于0,消失在水天交界處。這一案例,能夠培養(yǎng)學(xué)生的人文情懷和數(shù)學(xué)思想。
案例2:介紹定積分產(chǎn)生的歷史背景,介紹我國(guó)古代數(shù)學(xué)家劉徽的“割圓術(shù)”。“割之彌細(xì),所失彌少。割之又割,以至于不可割,則與圓周合體而無(wú)所失矣。”這是原始的積分思想。用“割圓術(shù)”求圓的面積以及周長(zhǎng)和圓周率,這一發(fā)現(xiàn)比歐洲早一千多年。
案例3:我國(guó)隋代趙州橋的曲拱,是用一塊塊直棱石料巧妙構(gòu)造的。這構(gòu)思奇特的趙州橋不但在世界橋梁史上留下了光輝的一頁(yè),而且閃耀著高等數(shù)學(xué)啟蒙思想的光芒,是微積分“以直代曲”思想的生動(dòng)體現(xiàn),也是微積分原理在建筑學(xué)上的樸素應(yīng)用。
分析:這兩個(gè)案例的介紹,既能使學(xué)生了解數(shù)學(xué)史,激發(fā)民族自尊心和自豪感,又能培養(yǎng)學(xué)生不怕困難、刻苦學(xué)習(xí)的精神。
2.曲邊梯形面積的求法——難點(diǎn)的處理
如何計(jì)算由曲線y=x2和直線x=0、x=1、y=0圍成的圖形面積呢?教師可引導(dǎo)學(xué)生利用趙州橋的“以直代曲”原理來(lái)解決問(wèn)題。
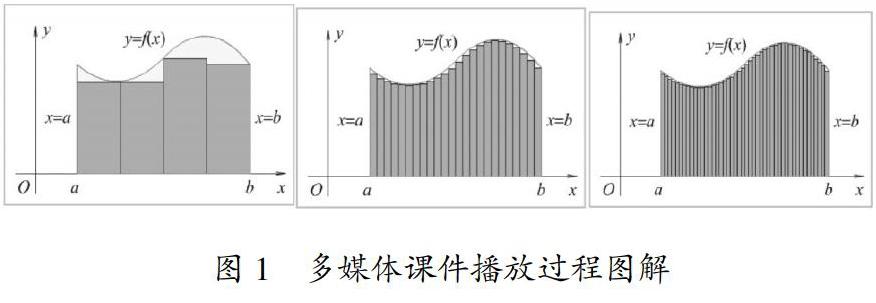
在直角坐標(biāo)系上畫(huà)出曲邊梯形,由y=f(x)>0、x=a、x=b、x軸所圍成說(shuō)明x軸稱(chēng)為底邊,曲線y=f(x)稱(chēng)為曲邊。問(wèn)題啟動(dòng):面積等于多少?幾何說(shuō)明直邊梯形的面積公式此時(shí)失效了,要求學(xué)生嘗試模仿劉徽的“割圓術(shù)”、趙州橋的“以直代曲”原理來(lái)求曲邊梯形面積,即由模仿到創(chuàng)新。創(chuàng)設(shè)情境如下:播放多媒體課件(見(jiàn)圖1)并要求學(xué)生觀察思考,在曲邊梯形內(nèi)擺滿小矩形,當(dāng)小矩形越來(lái)越多時(shí),小矩形面積之和與曲邊梯形面積之間的誤差將如何變化?組織學(xué)生展開(kāi)分組討論,不難得到“隨著矩形個(gè)數(shù)的增多,小矩形面積之和越來(lái)越接近于曲邊梯形的面積。顯然,分割得越細(xì),近似程度越高,誤差越小”。在學(xué)生討論的過(guò)程中,教師要求學(xué)生思考:如果在分割的時(shí)候采取等分區(qū)間而不是任意分割區(qū)間是否可以呢?通過(guò)教師的引導(dǎo),學(xué)生不難得出:因?yàn)橥茖?dǎo)論證過(guò)程要有嚴(yán)密性,所以不能以等分代替任意分割區(qū)間。這一過(guò)程,也是對(duì)學(xué)生的思維嚴(yán)謹(jǐn)性的訓(xùn)練。


在數(shù)學(xué)課程的學(xué)習(xí)中,高職學(xué)生的形象思維和小組合作能力毫不遜色本科學(xué)校的學(xué)生。教師通過(guò)“復(fù)習(xí)回顧、提出問(wèn)題、創(chuàng)設(shè)情境、分組討論、小組代表回答、教師總結(jié)歸納”這一師生互動(dòng)過(guò)程來(lái)講明本次課的教學(xué)難點(diǎn)——“曲邊梯形面積的求法”,能使學(xué)生更易于接受。以上難點(diǎn)的處理,也是為了說(shuō)明本次課的重點(diǎn):“定積分的幾何意義”的關(guān)鍵所在。教師通過(guò)模仿劉徽的“割圓術(shù)”、趙州橋的“以直代曲”原理來(lái)求曲邊梯形面積,即由模仿到創(chuàng)新,提高了學(xué)生歸納規(guī)律、解決問(wèn)題的能力。
3.定積分的定義——由歸納到演繹、由難點(diǎn)到重點(diǎn)的過(guò)渡


四、結(jié)語(yǔ)
總之,作為高職院校的數(shù)學(xué)教師,要充分認(rèn)識(shí)到數(shù)學(xué)教學(xué)中融入思想政治教育的重要性,深入挖掘數(shù)學(xué)學(xué)科中的思想政治教育資源,不斷將學(xué)生的思想政治教育工作滲透到自己日常的教學(xué)中。這樣,既能有效地調(diào)動(dòng)學(xué)生學(xué)習(xí)數(shù)學(xué)的積極性,又能真正做到“教書(shū)育人”,做學(xué)生成長(zhǎng)成才道路上的“指明燈”。
參考文獻(xiàn):
[1]李輝.基于數(shù)學(xué)課堂教學(xué)的思想政治教育初探[J].中國(guó)電力教育,2013(07).
[2]馬艷英,付彤,王青梅.將數(shù)學(xué)建模思想融入大學(xué)數(shù)學(xué)教學(xué)中的研究[J].吉林工程技術(shù)師范學(xué)院學(xué)報(bào),2018(09).
[3]張國(guó)勇.高職數(shù)學(xué)課程改革的認(rèn)識(shí)與思考[J].交通職業(yè)教育,2006(05).
[4]金晶晶.高職數(shù)學(xué)課程的思想政治教育功能研究[J].柳州職業(yè)技術(shù)學(xué)院學(xué)報(bào),2015(01).

