研究通性通法，突出高中數(shù)學核心和本質(zhì)

江蘇省蘇州市吳中區(qū)甪直高級中學 馮中芹

在高中時期，數(shù)學是比較難學習的一門課程，無論是學習文科還是學習理科，都會有一部分同學的數(shù)學成績不是很理想。造成這種現(xiàn)象的主要原因其實就是沒有掌握數(shù)學的理念以及衍生的基本數(shù)學運算技能，在這一點上，師生雙方都有一定的不足，針對如今這種現(xiàn)象，研究通性通法在高中數(shù)學中得到了運用，而且根據(jù)相關(guān)專家和學者的調(diào)查來看，研究通性通法在高中數(shù)學中的應(yīng)用已經(jīng)取得了一定的成效。本篇文章的主旨就是研究通性通法，突出高中數(shù)學核心和本質(zhì)。

一、通性通法的內(nèi)涵

例如，在當前的數(shù)學高考試題中，圓錐曲線問題往往會與直線方程相結(jié)合，在解題過程中，需要高中生把直線方程代入圓錐曲線方程中，這樣便能整理成為一個一元二次方程，此時那些簡單的數(shù)學知識就能得以運用了，例如判別式、求解公式、多個解與系數(shù)的關(guān)系等等，相關(guān)的專家和學者往往就利用這些簡單的知識編出許許多多精彩的數(shù)學試題。其實一道數(shù)學題可能會有多種解題方法，有些同學往往希望通過自己的學習掌握一道題目的多種解題方法，但是實際上高考數(shù)學往往淡化了一些特殊的解題技巧，因為這些特殊技巧的掌握其實會消耗老師和同學的很多時間，所以說刻意去追求特殊的解題方法并不是很好的選擇。

二、通性通法的大致特性

對于通性，我們可以這樣理解：如果滿足一切相關(guān)的知識理論，就歸納為通性。但這個概念過于籠統(tǒng)，如果將適合的理論概念全部涉入，也會使得“通性”這個概念變得繁重且復(fù)雜，所以，在這里我們對這些條件和理論進行區(qū)分和化解。首先，這些理論或者是知識、結(jié)論，對于教師和學生來說必須都是非常熟悉的、能夠通過學習去理解的，從這一點我們便不難看出，“通性”是具有熟知性的。此外，“通性”中的理論知識應(yīng)該能夠直接采用，并且在采用之后的能夠解決一系列的問題，而不是在特定情況下，這些理論知識才能去應(yīng)用，這無論對于教師還是高中生，都是十分不可取的。最后，“通性”一定要具有普遍性，理論知識的涵義必須是清晰的，不能讓學生或者教師理解起來是存在歧義和爭論的，這種普遍性我們也可以將其理解成為確定性質(zhì)。

對于通法，我們則可以這樣理解：字面意義上來解釋，“通法”即是能夠解決一類問題的方式方法，從某種意義上說就是“通性”結(jié)論產(chǎn)物，在泛指的意義上來說，通法是指解決問題的方法的一類。根據(jù)相關(guān)學者和專家的研究發(fā)現(xiàn)，通法可以適用于一類的問題上，所以，“通法”具有適用性。另外，“通法”是“通性”的衍生物，所以它對“通性”的依賴性很強，但是在熟練運用之后，我們就可以單獨采用“通法”而不用再去“通性”中驗證一番，所以，在一定程度上“通法”是具有有序性的。最后，因為時代在不斷發(fā)展，數(shù)學高考也要順應(yīng)時代進行發(fā)展和改變，因此“通法”還要適應(yīng)時代進行一定的升級和改變，但是“通法”在整體上還是適用的，故而“通法”還具有一定的穩(wěn)定性質(zhì)。

三、通性通法理論的初步界定

通過上述文章中對通性通法進行拆分理解，其實我們就很容易對二者進行理解了。對于現(xiàn)階段的通性通法，我們依然沒有對其進行整體界定，這不僅僅是因為通性通法在時代中是不斷進化和發(fā)展的，而且還因為通性通法的范圍比較寬泛，其不僅可以涉及高中數(shù)學，還涉及其他的學科，甚至還能涉及其他的學術(shù)范圍中。經(jīng)過多年的研究，許多專家和學者憑借豐富的知識已經(jīng)對其進行了初步的界定，其發(fā)揮的作用是令每一個人都想不到的。接下來我們將對此進行詳細闡述，由于其在高中數(shù)學的表現(xiàn)比較明顯，我們將以江蘇省2017 年的高中數(shù)學試題作為例子進行參考。

例如，2017 年江蘇省數(shù)學高考試題的填空題第三題：某工廠生產(chǎn)甲、乙、丙、丁四種不同型號的產(chǎn)品，產(chǎn)量分別為200，400，300，100 件，為檢驗產(chǎn)品的質(zhì)量，現(xiàn)用分層抽樣的方法從以上所有的產(chǎn)品中抽取60 件進行檢驗，則應(yīng)從丙種型號的產(chǎn)品中抽取_____件。

同張試卷的必做題二十三題：已知一個口袋有m個白球，n個黑球（m,n∈N,n≥2）,這些球除顏色外全部相同。現(xiàn)將口袋中的球隨機逐個取出，并放入如下所示的編號為1,2,3，……，m+n的抽屜內(nèi)，其中第k次取球放入編號為k的抽屜（k=1,2,3，……，m+n）。

1 2 3…m+n____

（1）試求編號為2 的抽屜內(nèi)放的是黑球的概率P；

（2）隨機變量X的概率分布為：

X images/BZ_8_1614_2546_1631_2563.pngimages/BZ_8_1737_2546_1753_2563.png……images/BZ_8_2226_2546_2243_2563.pngP ……

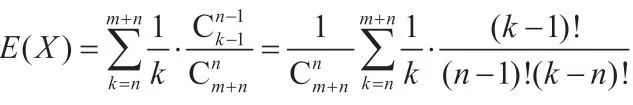
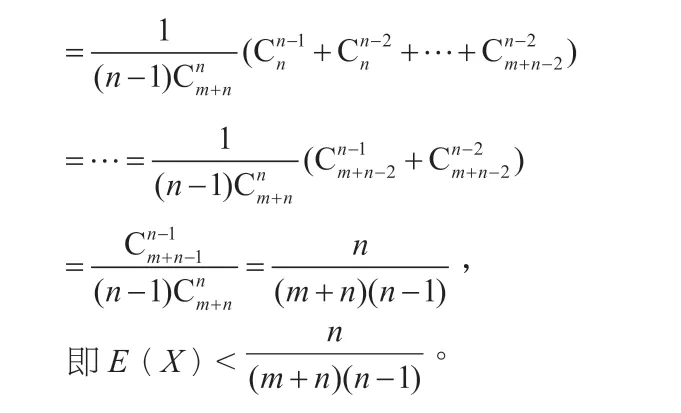
這兩道高考數(shù)學題考查的是古典概率、隨機變量及其分布、數(shù)學期望等基礎(chǔ)知識，第一道填空題比較簡單，只是考查了簡單的概率問題，后一道大題就考查了組合數(shù)及其性質(zhì), 考查運算求解能力和推理論證能力。兩道題固然在本質(zhì)上有一些不同之處，但是可以用通性通法的方法解決，因為兩道題是互相關(guān)聯(lián)的。另外，學生在高考這樣重大的考試中難免緊張，都有可能一時忘掉其解法，這時學生如果熟知通性通法的基本概念，就可以由其中一道題推算出另一道題目的解法，而且，后一道大題這里只給出了一種解法，學生還可以通過向公式代入數(shù)值的方式進行解答。所以說如果能將通性通法進行一定的界定，對于學生的數(shù)學知識掌握是大有裨益的。

眾所周知，笛卡兒所創(chuàng)立的解析幾何思想可以說是整個數(shù)學界發(fā)展過程中的一次巨大飛躍了，通過將坐標和方程結(jié)合的方式，使得代數(shù)與幾何圖形完美地結(jié)合在一起，這種方式不僅充分發(fā)揮了幾何直觀形象以及能夠進行推理演算的優(yōu)勢，還能夠?qū)⒋鷶?shù)精確運算的價值運用其中，大大節(jié)省了解決數(shù)學問題的時間。由此可見，幾何思想是數(shù)學通性通法的具體表現(xiàn)。這一點從江蘇省數(shù)學高考試題的18 題中便夠體現(xiàn)出來：

如圖1，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱臺形玻璃容器Ⅱ的高均為32cm，容器Ⅰ的底面對角線AC的長為10 cm，容器Ⅱ的兩底面對角線EG，E1G1的長分別為14cm 和62cm。分別在容器Ⅰ和容器Ⅱ中注入水，水深均為12cm。現(xiàn)有一根玻璃棒l，其長度為40cm。（容器厚度、玻璃棒粗細均忽略不計）

（1）將l放在容器Ⅰ中，l的一端置于點A處，另一端置于側(cè)棱CC1上，求l沒入水中部分的長度；

（2）將l放在容器Ⅱ中，l的一端置于點E處，另一端置于側(cè)棱GG1上，求l沒入水中部分的長度。

圖1

如圖2，記玻璃棒的另一端落在CC1上點M處。

記AM與水面的焦點為P1，過P1作P1Q1⊥AC，Q1為垂足，

則P1Q1⊥平面ABCD，故P1Q1=12，

答：玻璃棒l沒入水中部分的長度為16cm。

( 如果將“沒入水中部分”理解為“水面以上部分”，那么結(jié)果為24cm)

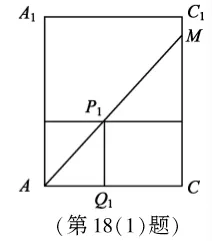
圖2

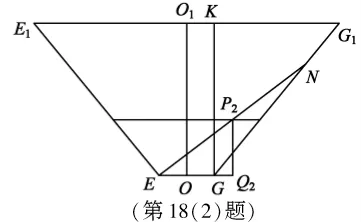
圖3

（2）如圖3，O，O1是正棱臺的兩底面中心.

由正棱臺的定義知，OO1⊥平面EFGH， 所以平面E1EGG1⊥平面EFGH，O1O⊥EG。

同理，平面E1EGG1⊥平面E1F1G1H1，O1O⊥E1G1。記玻璃棒的另一端落在GG1上點N處，

過G作GK⊥E1G，K為垂足， 則GK=OO1=32。

因為EG= 14，E1G1= 62，

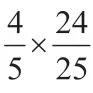
答：玻璃棒l沒入水中部分的長度為20cm。

在這道題目中，兩個容器便是幾何圖形，其中對于情境的變化時時刻刻在牽動著數(shù)學通法的改變。這道題目中的幾何圖形都有著很好的幾何性質(zhì)，所以與其相關(guān)的數(shù)學問題可以借助平面幾何知識來解決，而當這些圖形組合演變成一個幾何體時，就要依靠我們比較熟悉的代數(shù)運算的力量了，這道題目中的代數(shù)運算可以研究幾何圖形的性質(zhì)，在解題過程中，學生也利用圖形的性質(zhì)進行簡化計算，二者互為共生，體現(xiàn)了數(shù)學當中的“數(shù)”與“形”的結(jié)合。

四、高中數(shù)學對于通性通法的外延界定

經(jīng)過高中數(shù)學對通性通法進行了初步界定之后，此后通性通法的發(fā)展就有了一定的參照物，發(fā)展過程也就變得更加具有方向感。由前文我們不難得知，高中數(shù)學知識當中的明確定理、概念以及推論是可以歸納到通性之中的，而這些定理、概念以及推論之下的方法是可以歸納到通法之中的。但是許多公式并不是在定理中或者推論中得出來的，在高中生的日常數(shù)學計算中，這些公式的應(yīng)用非常頻繁，因此，這些公式也能歸納到通性通法當中。

五、由通性通法得出的高中數(shù)學的核心和本質(zhì)

一道高中數(shù)學題可能會有多種解法，但我們要求的是著重一種解法。在這里許多師生可能會有一定的誤解，我們進行詳細的解釋。一道數(shù)學問題是有多種解法的，而這些解法在難度上就會有高有低，有些是運用基本的通性通法的理論知識，而剩下的比較難的方法大多都是需要高中生采用一些不屬于通性通法的內(nèi)容進行解答，但是比較難的解答方式方法的思維過程比較新穎，另辟蹊徑，有些同學不易想到。重視通性通法并不是強行學會比較難的解題方法，而是在學會一種基礎(chǔ)解題方法的基礎(chǔ)上再掌握另一種基礎(chǔ)解題方式，切勿還未學會走路就要自行奔跑，這在高中數(shù)學的學習上是十分不可取的一種行為。所以，無論是高中生還是高中數(shù)學教師，都要重視通性通法，并將其進行應(yīng)用。

在高中數(shù)學中，通性通法的概念已經(jīng)得到了初步的界定，而在高中數(shù)學中應(yīng)用通性通法的概念，從某一方面來說也是在強調(diào)高中數(shù)學的重要性，突出高中數(shù)學的核心和本質(zhì)。