高中數學必修3中算法的典型例題的Matlab實現

劉本虹 申艷玲 鄭艷萍

一、引言

高中數學3是高中數學必修中的五個模塊之一，它包括算法初步、統計和概率三章內容。算法是數學與其應用的重要組成部分，是計算科學的重要基礎，是連接解決問題方法與計算機能夠理解的程序語言之間的橋梁，是現代人必須具有的數學修養[1]。Matlab是Mathworks公司開發的用于概念設計、算法開發、建模仿真、實時實現的集成環境。其廣泛運用于生物醫學工程、圖像信號處理、信號分析、電信、時間序列分析、控制論和系統論等領域[2]。在國內高校數學專業開設的多種課程都涉及到Matlab的應用，比如數學與應用數學專業開設的《數值分析》《數學建模》，信息與計算科學專業開設的《數值逼近》《數值代數》《微分方程數值解》等，許多課程中的數值實驗部分都需要用Matlab編程實現。

對于本科生來說，開始接觸算法的相關課程不太適應。主要原因在于一方面無法理解算法語；另一方面不太理解程序語言。因此，盡早地讓高中生接觸一些簡單算法，并把算法用Matlab或Mathematica編程實現是非常有必要的，可以很好地實現高中到大學本科相關課程銜接。

二、主要內容

本節內容主要選取或改編于[1]中出現的典型算例及其編程實現。

例1.編寫程序，使任意輸入的n個整數按從大到小的順序輸出。(該例題改編于[1]中第一章的例7)

在Matlab中有現成的命令對數的大小進行排列，本文為了讓學生更好地理解算法，從而遵照教材所給的算法分析予以Matlab編程，學生可以看到運算每一步的結果，加深對照程序語言的理解與應用。

算法分析：

把這n個數以向量形式輸入，依次比較各分量的大小，進行排序。

以下是比較-1；5；300；3002；-5000；119；-100的大小，且按從大到小的次序輸出。其Matlab程序及運行結果如下。

以下算法案例均來自[1]中第一章第3節中的案例。

例2.輾轉相除法

輾轉相除法是一種古老而有效的求兩個正整數的最大公因子的算法之一，這種算法是歐幾里得在公元前300年左右首先提出的，因而又叫歐幾里得算法[1]。

算法分析：

第一步：給定兩個正整數m，n；

第二步：計算m除以n所得到的余數r；

第三步：m=n，n=r；

第四步：若r=0，則m，n的最大公約數等于m；否則，返回第二步。

其Matlab程序如下：

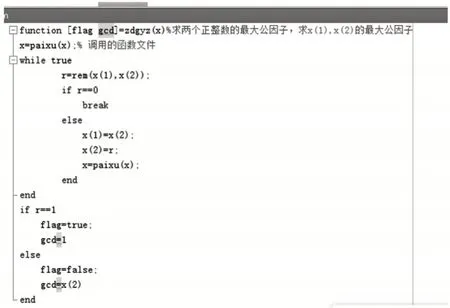
注：Matlab中也有內置命令gcd(x,y)可求兩個正整數x,y的最大公因子。

例3.更相減損術

更相減損術是《九章算術》中求兩個數的最大公約數的方法，其編程結構類似于輾轉相除法，唯一區別是前者做除法，后者做減法。其Matlab程序如下：

分別以m=98，n=63為例，其運算結果如下：

這個運算過程與[1]第一章第3節例1所給的運算過程：

98-96=35；63-35=28；35-28=7；28-7=21；21-7=21；21-7=14；14-7=7是一致的。

例4.秦九韶算法

我國南宋時期的數學家秦九韶(約1202～1261)在《數書九章》中對多項式

f(x)=anxn+an-1xn-1+L+a1x+a0

的求值提出如下算法：

把多項式f(x)改寫為：

f(x)=an xn+an-1xn-1+L+a1x+a0

=(anxn-1+an-1xn-2+L+a1)x+a0

=((an xn-2+an-1xn-2+L+a2)x+a1)x+a0

=L

=(L(an x+an-1)x+an-2)x+L+a1)x+a0

求多項式值時，首先計算內層括號內一次多項式的值，即

v1=an x+an-1

然后由內向外逐層計算一次多項式的值

v2=an x+an-2

v3=v2x+an-3

L

vn=vn-1x+a0

這樣，求n次多項式f(x)的值就轉化為求n個一次多項式的值。

據此算法計算f(x)=4x5+2x4+3.5x3-2.6x2+1.7x-0.8當x=5時的值[1]。

Matlab程序及運行結果如下：

例5.進位制

進位制是人們為了計算數和運算而約定的計數系統。下面以[1]中的例題：設計一個算法，把k進制數a(共有n位)化為十進制數b。

算法分析：

第一步：輸入a,k,n

第二步：b=0,i=1

第三步：b=b+aiki-1,i=i+1

第四步：判斷i＞n是否成立。若是，執行第五步；否則，返回第三步。

第五步：輸出b。

注：ai為k進制數a右數第i位數。

下面編程把1011001轉換為十進制，該例題改編于[1]中第三章第3節的例5。

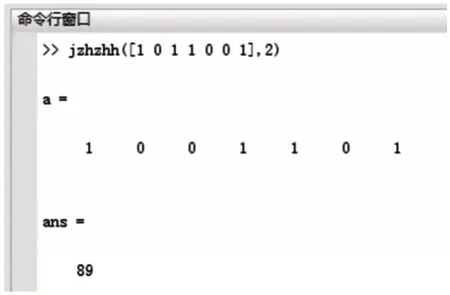
三、總結

本文搜集了數學必修3中涉及到的典型算例，結合教材上的算法分析，用matlab進行算法實現，直觀呈現運行結果，依此希望對高中生對數學算法的理解有所幫助。