基于時變T-Copula 模型的期貨合約相依關系研究

康 龍

（柏林國際應用技術大學 工商管理學院，德國 柏林10587）

一、引言

近年來，我國金融市場發展迅速。全國范圍的四個期貨交易所中，有許多新的期貨合約上市交易。交易合約數和交易總量都達到了十分可觀的規模。以上海期貨交易所為例，從1999 年到2017 年，單邊年成交量由0.03 億手增長到13.64 億手，增長454倍；單邊年成交金額由0.24 萬億元增長到89.94 萬億元，增長374 倍①。上市期貨品種由1999 年的3個增加到2018 年的15 個（含原油期貨）。各大期貨交易所還增添了基于某些期貨品種的期權交易，為各類投資者提供了更多的交易工具。例如，目前上海期貨所有銅期權交易和天然橡膠期權交易。

不斷增長的合約品種和交易量也給交易所的風險控制帶來了新的問題。隨著交易合約品種的增多，更多的投資者開始同時交易多種期貨及其他衍生品合約，這就給交易所在計算和收取客戶保證金方面帶來了新問題。一方面，投資者希望在交易每種合約的時候繳納較低的保證金，提高交易杠桿的同時，提高資金的使用效率。另一方面，交易所希望在收取合理保證金的前提下，不過度收取客戶的多余保證金，通過提高客戶的資金使用效率來增加整個市場的交易量，并提高市場活躍度。由于大多數客戶同時交易多種合約，且各個合約的相依關系不同，當合約之間可以對沖部分風險的時候，客戶整體賬戶的保證金就不需要設定為單獨交易每種合約所交保證金的總和，從而在收取合理保證金的同時釋放多余的保證金給客戶。怎樣才能較為準確地估測和計算每個交易多種合約的客戶所須繳納的保證金呢？對于這個核心問題，時變T-Copula 模型為我們提供了一個較為可行且效果良好的量化解決方案。本文運用該模型對上海期貨交易所交易的12 種主力期貨合約價格變化的日內數據進行估測，結果顯示模型可以較好地描述各種期貨合約之間的相依關系。

二、文獻綜述

金融合約的相依關系一直是實證研究的一個重點，其研究結果主要運用于風險管理、投資管理以及各種套保或套利的交易策略優化。例如，梁仁方等[1]運用Copula-CoVaR 模型研究原油期貨與PTA 期貨的風險溢出效應。謝赤等[2]運用時變Copula 模型研究滬深300 股指期現貨高頻價格相依結構測度。在金融合約的相依關系方面，Copula 模型比多元正態分布能夠更加靈活地描述某些特定的相依關系，比如明顯的尾部相依性或者非對稱的相依關系。因此，Copula 模型結合GARCH 模型被廣泛運用于描述多種金融合約的相依關系。

Copula-GARCH 模型最早由Jondeau et al.[3]和Patton[4-5]開始使用。為了度量時變時間序列的條件相關性，Jondeau et al.[3]使用了Copula 函數并將其系數指定為前期變量的函數。Jondeau et al.[3]還用Hansen[6]文章中的GARCH 模型來擬合數據的邊際分布。在他們的模型中偏度系數和峰度系數都是時變的。他們在文中發現對于大多數金融數據，時間序列之間的相依性在市場較大波動后，尤其是市場大幅下跌后會顯著攀升。此外，Patton[4]還運用類似的模型對大盤股指數與小盤股指數的非對稱的相依性進行了研究，并檢驗這種非對稱的相依關系對投資組合是否有顯著影響。Hu[7]運用混合Copula 模型研究了主要股票市場指數的相依性。她在模型中給正態Copula、Gumbel's Copula 和扭轉Gumbel's Copula不同權重并加和來形成新的Copula 形式。Jondeau et al.[8]運用T-Copula 描述兩個股票指數的相依性，Copula 系數遵從雙狀態馬可夫過程。

通常描述多維聯合分布的相依關系是比較困難的。Garcia et al.[9]構建了一個多維Copula 模型來描述四種資產的價格變化的相依關系。他在模型中運用了狀態轉換（regime-switching）的構造，在其中一個狀態（regime）中他運用了多維正態Copula，在另一個狀態中運用了混合Copula。在其混合Copula中，每一個Copula 側重于描述每對特定資產價格組合的相依關系。Savu et al.[10]運用分級形式的Archimedean Copula，這種形式的Copula 在一定程度上可以靈活描述各個價格組合的相依關系。在模型中，每一對關系緊密的價格被一個特定類的Archimedean Copula 所描述，然后在上層運用其他Archimedean Copula 來連接先前部分。Archimedean Copula 的一個很好的特性是在這種分級的結構下，最后上層生成的函數形式依然滿足Copula 函數的定義。

但過多的系數也給Copula 模型的估測帶來了很大的困難。最大似然法在理論上可以用于估測Copula 模型。然而，在實際中當所擬合的時間序列增多的時候，在估測過程中最大似然法的數值優化問題將會很難得出滿意的結果。Joe et al.[11]提出了一種兩步估測法。第一步用最大似然法估測各個時間序列邊際分布的系數，第二步再用最大似然法估測Copula 函數部分的系數。Joe[12]證明了在常規條件下，這種兩步估測法產生的估測值是一致的，并且漸近服從正態分布。Patton[13]也得出了相似的結論。另外，在第一步估測中，我們還可以不估測邊際分布的具體系數，而采用實證法來估測邊際分布。這種方法可以避免錯誤假設邊際分布的問題，被Cherubini et al.[14]稱為典范最大似然法（Canonical Maximum Likelihood）。Hu[7]使用這種估測方法并將其命名為半參數法，并基于Genest et al.[15]，她證明了這種半參數法的估測值是一致的，并且漸近服從正態分布。另外，Copula 模型還可以用無參數法來估測。Deheuvels[16]介紹了實證Copula 的定義并且證明了實證Copula 一致性收斂于真實的Copula 形式。Xu[17]闡明了Copula 模型可以用貝葉斯的方法來估測。

三、模型

Copula 模型在金融建模方面已經得到廣泛的應用。它的獨到之處在于能夠將多元隨機變量的聯合分布，分解為各自隨機變量的邊際分布和一個連接這些邊際分布的Copula 函數。也就是說，為了構建正確的多元隨機變量的聯合分布，我們可以先對每一個隨機變量單獨建模，找到一個最好地描述其邊際分布函數的模型，然后再尋找一個最合適的Copula 函數形式來連接這些邊際分布。Copula 函數具有很多形式，T-Copula 函數雖然不是最完美的，但是對于同時描述大量的隨機變量的相依關系，確實是一個很不錯的選擇。它比正態Copula 函數能更加靈活準確地擬合現實的金融數據。T-Copula 模型主要可用于風險管理和量化投資。本文主要運用Copula 函數結合GARCH 模型來對多種期貨合約的價格變化的聯合分布進行建模估測。

（一）Copula 函數

Copula 函數是一個多元分布函數，而被描述的多元隨機變量的每一個邊際分布是這個多元函數中的變量。Copula 函數將所有的邊際分布連接起來形成多元隨機變量的聯合分布。Copula 理論主要基于Sklar[18]的結論，我們在下邊敘述針對連續邊際分布的Sklar's 定理。

令F1（x1），…，Fn（xn）分別為x1，…，xn的連續邊際分布函數。令H 為（x1，…，xn）的聯合分布。那么存在一個唯一的Copula 函數滿足以下條件：

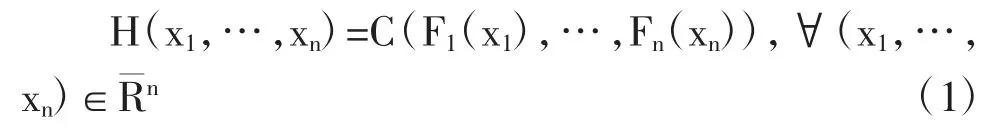
相反，如果我們令F1（x1），…，Fn（xn）為連續邊際分布函數且C 為一個Copula 函數，那么，由等式所定義函數H 是一個聯合分布且其各個邊際分布分別為F1（x1），…，Fn（xn）。

根據以上理論，我們可以將一個多元隨機變量的聯合分布，分解為每個隨機變量的邊際分布和連接他們的Copula 函數。相反，這個理論也說明要建立一個多元隨機變量的聯合分布，可以先為每一個隨機變量找到一個最合適的邊際分布，然后再尋找一個最合適Copula 函數來連接所有的邊際分布。另外，為了更好地擬合數據，我們通常假設隨機變量分布的矩是時變的并且依賴于過去的變量數值。所以，在時間t 的隨機變量的聯合分布將變成基于過去變量數值的條件分布。這樣以上所述的Copula 理論則需要進一步擴展為在條件分布情況下的理論。

（二）邊際分布

作為組建Copula 模型的第一步，我們需要為每一個合約的價格變化的邊際分布，找到最合適的模型。因為選用錯誤的模型來描述邊際分布，將會導致錯誤的聯合分布。令xi，t為資產i 在時間t 的回報率，那么它的條件均值和條件方差服從以下描述。

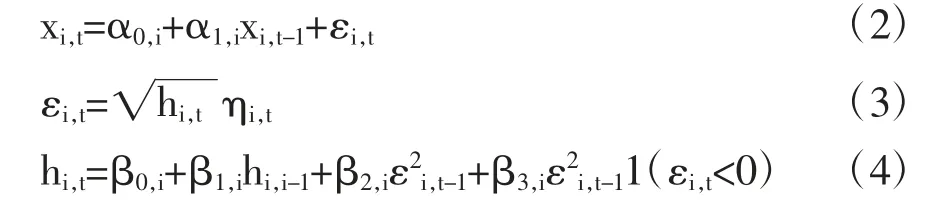
在等式（2）到（4）中，我們用AR（1）過程來描述條件均值，并用一個GJR（1，1）構造來描述條件方差[19]。以上等式中的系數有以下限制：β0，i＞0，是一個指示函數，當εi，t-1＜0 時，此函數值為1，否則為0。以上模型可以足夠好地描述每個所包含資產回報率的邊際分布。當然，也可以在等式（2）到（4）中包含更多的外因解釋變量，從而更好地描述數據。另外，我們假設ηi，t在時間軸上服從i.i.d.并且服從學生t 分布，自由度系數為νi。當然我們還可以進一步描述條件高階矩，例如，Hansen[6]、Jondeau et al.[8]假設GARCH 模型中的殘差服從偏t 分布，并且發現偏t分布比正態分布能更好地描述金融數據。我們可以假設ηi，t～SkewedT（ηi，t｜νi，t，λi，t）。其中，ηi，t均值為0，方差為1，νi，t為自由度系數，λi，t為偏度系數。兩個系數νi，t和λi，t隨時間而變，且非線性依賴于前期的解釋變量。

（三）相依結構

正態Copula 和學生T-Copula 同屬于橢球分布族，他們經常被用來描述多元隨機變量的聯合分布。在實際應用中，通常學生T-Copula 比正態Copula 系數結構更加靈活，能夠更好地描述多元隨機變量之間的相依關系，尤其在擬合金融數據的應用中[20]。令Tν-1為標準學生t 分布Tv的逆分布，其自由度系數為ν＞2。TR，ν為n 維學生t 分布，其相關系數矩陣為R，自由度系數為ν。那么，n 維學生T-Copula可以定義如下：

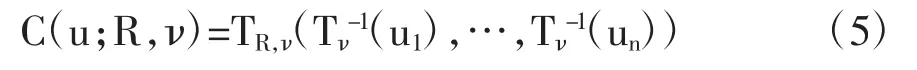
且其密度函數可定義為：

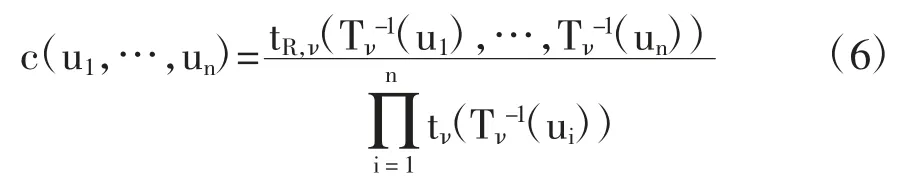
其中，tν和tR，ν分別為Tν和TR，ν的概率密度函數。

我們借助DCC-GARCH 模型的思路[21]，可以構建一個時變T-Copula，其時變相關系數矩陣由以下等式來描述：

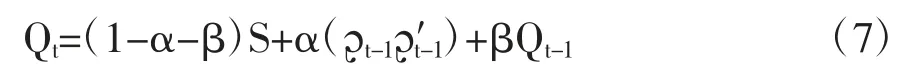
另外，等式（7）確保條件相關系數矩陣Rt是正定的[22]。

（四）模型估測

令Θ=｛θ，γ1，…，γn｝為聯合分布的系數集，其中θ 為Copula 部分的系數，γi是第i 個資產價格的邊際分布的系數集。那么，所有n 個價格在時間t 的條件累計分布函數為：

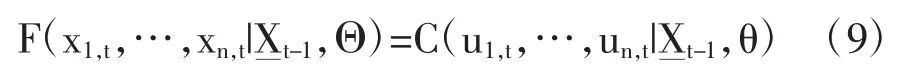
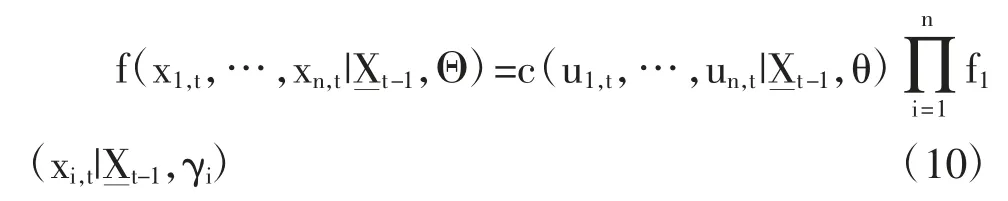
基于等式（10），對數似然函數值可以寫成：

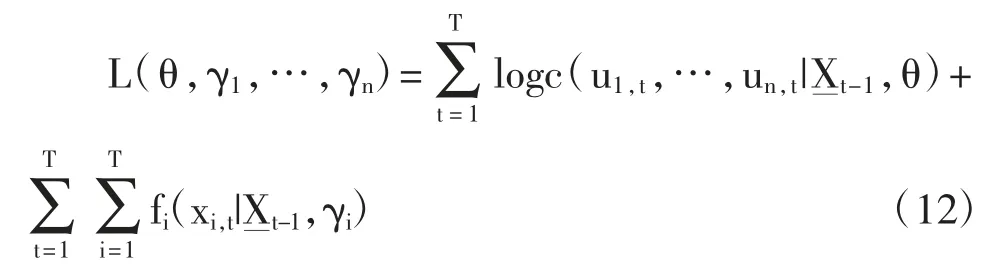
等式（12）顯示出Copula 和邊際分布是相加性可分的。所以我們可以運用兩步法估測整個模型。第一步，用最大似然法估測每個變量的邊際分布的系數，然后再基于第一步的估測得出的每個價格變化的累計分布函數，用最大似然法估測Copula 的系數。Joe et al.[12]和Patton[13]都論證了這種兩步法的估測值是一致的，且漸進服從正態分布。

本文先用最大似然法估測每個價格序列的GJR（1，1）模型，然后估測時變T-Copula 的系數。對于T-Copula 的最大似然法估測通常得不出分析解，并且數值法最大化問題也十分困難。我們遵循Chen et al.[22]的辦法，基于，可以計算出的樣本協方差矩陣，這個樣本協方差矩陣是自由度ν 的函數。先設定，可以運用等式將Qt和Rt在所有時間t 的數值表述為α，β 和ν的函數，然后通過最大化T-Copula 密度的對數似然值來估測α，β 和ν。

四、數據來源

本文擬合的數據為上海期貨交易所交易的12種期貨主力合約20 分鐘的價格變化（對數回報率）。我們運用AR（1）來描述條件均值，然后用GJR（1，1）來描述每一個價格變化的條件波動率[19]。在運用TCopula 函數形式的時候，我們用一個時變相關系數矩陣來描述各個變量之間的動態相依關系[21]。由于所需估測的系數比較多，直接用最大似然法估測很難得到滿意的結果。我們采用兩步法來估測，第一步估測每個合約價格變化的邊際分布模型，第二步估測Copula 函數中的系數。

目前在上海期貨交易所交易的期貨合約共有14 個品種，分別為銅、鉛、鋁、鋅、錫、鎳、天然橡膠、瀝青、螺紋鋼、熱卷、黃金、白銀、燃料油和線材。由于燃料油和線材交易十分不活躍或者交易時長不滿1 年等原因，在分析中不考慮這兩個品種②。具體數據的時間跨度為2018 年1 月2 日至2018 年12 月28 日。由于我們所描述的數據頻率為20 分鐘，所以1 年長度的數據可以提供足夠的樣本數量用于估測。而且1 年長度的數據也可充分包括數據中的大部分的季節性因素。本文的原始數據來源于國內某大型期貨公司量化交易柜臺實時獲取的高頻數據，數據頻率為0.5 秒。我們對每一個交易品種在每一天按照最大持倉量的原則選取主力合約，然后將每個品種的主力合約連接起來形成整體數據。所有12個品種的主力合約的價格按照接收行情的時間戳對齊。通常對于每一個相對交易比較活躍的合約價格，每0.5 秒交易所都會發送新的行情價格。而對于某些交易不活躍的合約或者某些活躍合約在極少數不活躍的時間段，在某些0.5 秒的時間段中交易所不會推送任何行情。我們根據數據中的買價和賣價算出中間價，再選出20 分鐘頻率的價格來計算價格變化。如果恰巧在所選的時間點上沒有數據，我們將用前后最近的價格均值來代替。另外，由于每種合約夜盤交易時段有所不同且模型估測的核心在于所有合約的聯合分布，夜盤時段只采用所有合約都進行交易時段的數據。最后，所擬合的價格變化具體為每20 分鐘價格的自然對數的一階差分，當交易停止時或者主力合約更換的時候，就會產生異常值。為了避免給整個模型估測帶來問題，我們將交易中斷或主力合約更換期間的價格變化值都設為0。

五、實證結果

（一）數據的初步分析

同一品種合約在不同時期有不同的波動率，而且具有明顯的波動率聚集現象。即使在排除了交易間斷過程（包括更換主力合約等情況）的價格大幅度波動的情況下，某些品種的價格變化仍有超常規的跳動。表1 顯示了12 個期貨品種對數回報率的描述性統計量，分別為均值、標準差、偏度和峰度。所有品種回報率趨近于0，標準差在0.000 8 到0.004 1 之間。其中，天然橡膠波動率最高，黃金最低。12 個品種的偏度在-0.58 到0.52 之間。12 個品種的峰度都明顯大于3，充分說明了所有回報率分布的厚尾性。根據以上的初步分析，采用GARCH 模型來描述回報率的波動率聚集和分布的厚尾性。

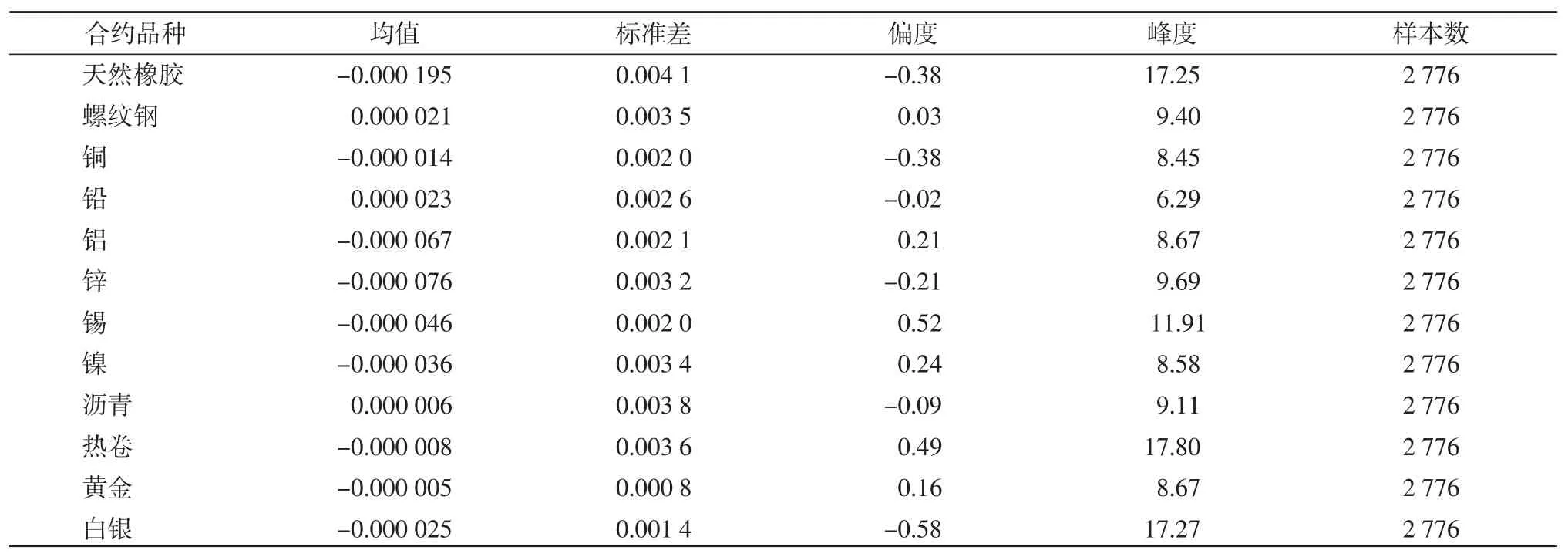
表1 12 種期貨合約20 分鐘對數回報率的統計描述

（二）邊際分布的估測

在估測每一個合約的邊際分布時，本文采用了AR（1）過程和GJR（1，1）模型來描述價格變化的條件均值和條件方差。在實際應用中，可以加入更多外生變量來提高模型的擬合和預測效果③。表2 顯示了單個合約邊際分布的估測結果。對于條件均值等式，除了銅、鉛、瀝青、熱卷和黃金，其他品種的第一個滯后項的系數都是統計上顯著的。說明AR（1）可以較好地描述合約的條件均值。在條件方差方面，對于絕大多數合約的描述，GARCH 和ARCH 項的系數是統計上顯著的。然而，對于杠桿項，有很多合約的系數并不是統計上顯著的，或許GARCH（1，1）的模型會比GJR（1，1）的模型能夠更好地描述一部分期貨合約的價格變化④。另外，大部分合約的自由度系數都是統計上顯著的，并且估測數值比較小，充分說明合約具有顯著的厚尾性。我們可以根據模型估測結果，繪制12 個合約估測的條件波動率。對于20 分鐘間隔的價格變化，可以明顯觀測到波動率的積聚性以及波動率突發升高的現象。這也充分說明了，交易所加強日內價格變化的風險控制的重要性和必要性。

（三）時變Copula 函數的估測

表3 列示了Copula 函數的估測結果。基于標準誤差，Copula 函數的三個系數都是統計上顯著的。系數α 的估測值非常接近于0，系數β 的估測值非常接近于1，而自由度系數ν 的估測值大約為23。T-Copula 函數的自由度系數的估測值體現了TCopula 同時描述多組合約價格變化的相依關系時的相對表現。由于T-Copula 的自由度系數很大程度決定了所描述的各個組合期貨合約的尾部相依度，在擬合大量合約的情況下，有些合約之間尾部相依度較高，有些則較低，T-Copula 自由度系的估測值也是同時描述較高和較低尾部相依性的一種折中。所以，T-Copula 可以在一定程度上更好地描述多種價格變化的相依關系[20]。

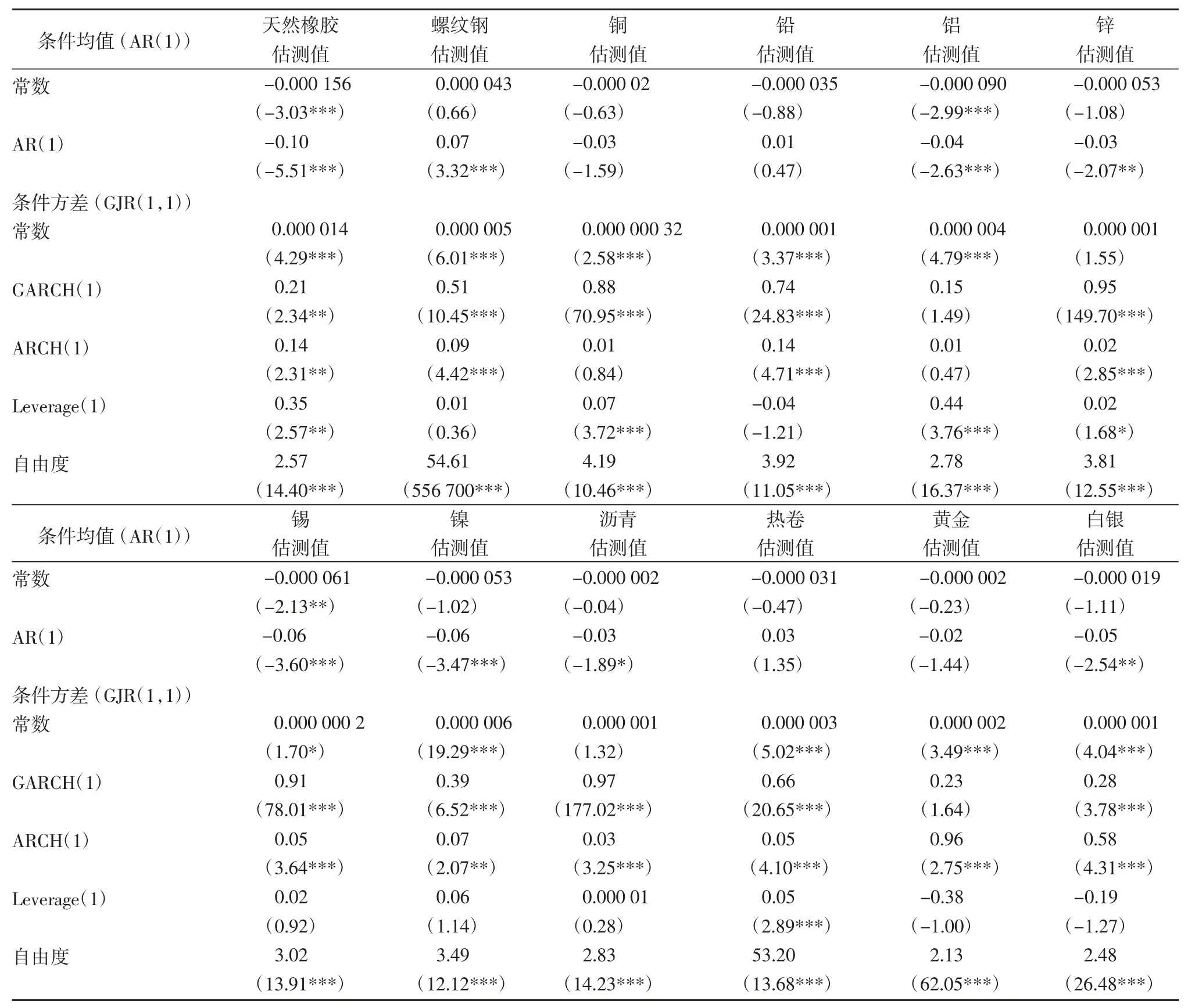
表2 12 種期貨合約邊際分布的估測結果

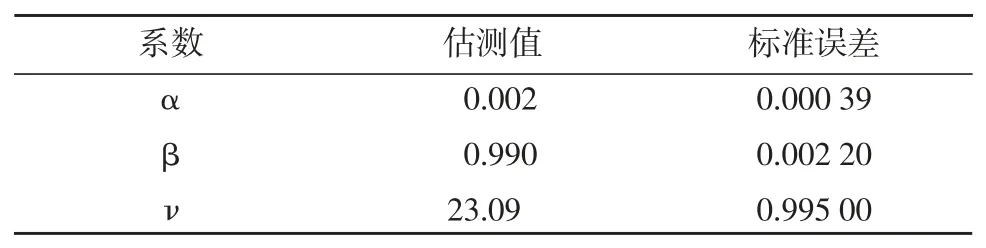
表3 時變T-Copula 函數中系數的估測值及其標準誤差

（四）時變相依關系

時變T-Copula 模型的相關系數矩陣和自由度系數可以比較好地同時描述多種合約價格變化的相依關系，尤其是在一定程度上可以較好地描述每兩個合約之間的尾部相依關系。圖1 繪出了螺紋鋼和熱卷、黃金和白銀、銅和鎳、銅和錫、錫和白銀、橡膠和瀝青，這6 組合約的動態相關系數。前3 組合約品種由于屬于相同或者相近的合約類別，他們的相關系數均超過0.5，而后3 組合約屬于不同的類別，他們的相關系數均低于0.5。同時，可以發現在時變的動態模型構造下，各組合約之間的相關系數時變性還是很明顯的⑤。圖2 繪出了上述6 組合約的尾部相依系數（tail dependence coefficient）。螺紋鋼和熱卷這對合約的尾部相依系數在0.3 左右波動，可見這兩種產品的尾部相依關系是多么的密切。而黃金和白銀、銅和鎳，這2 組合約的尾部相依系數在0.03 左右波動。后3 組非同類或接近同類的合約組合尾部相依系數都幾乎接近于0。由于模型的時變屬性，尾部相依系數也是一直在波動的。以上結果充分說明了，時變T-Copula 模型可以在一定程度上同時描述多種合約的相依關系，尤其是尾部的相依關系。

六、結論與展望

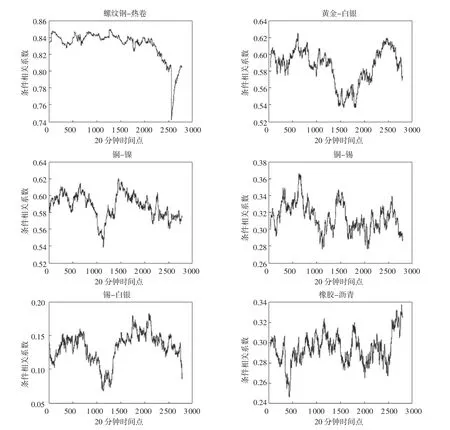
圖1 6 對期貨合約的估測條件相關系數

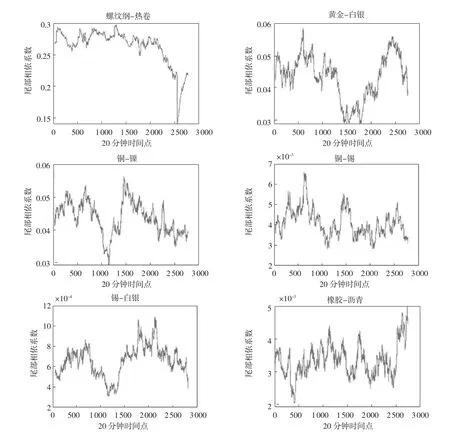
圖2 6 對期貨合約的估測尾部相依系數

基于時變T-Copula 模型，本文構建和估測了期貨合約相依關系。第一，用AR（1）過程和GJR（1，1）模型來描述每個合約價格變化的條件均值和條件方差。第二，用時變T-Copula 模型來連接每個合約的邊際分布，從而描述它們的相依關系。在時變TCopula 模型中，時變的相依關系主要由時變的相關系數矩陣和自由度系數來共同描述。本文運用一個動態條件相關系數（DCC）的構造，來實現隨時間變化的相依系數矩陣。估測結果顯示，對于上海期貨交易所12 個期貨品種的主力合約在2018 年所有交易日的20 分鐘價格變化數據，此模型可以較好地描述邊際分布和聯合分布。但GJR（1，1）模型中的杠桿效應不是十分顯著，這也意味著用GARHCH（1，1）模型代替GJR（1，1）模型或許更加合適。在相依關系的描述方面，本文繪制了6 組合約估測的條件相依系數和尾部相依系數。時變T-Copula 模型可以很好地同時描述多個合約價格變化的相依關系，尤其是顯著的尾部相依性。

在理論上講，很難找到一個Copula 函數形式能夠足夠靈活地同時描述很多變量的相依關系。本文中所構建的時變T-Copula 模型也具有一定的局限性。此模型的系數結構對于每一對所包含的隨機變量，其產生的尾部相依系數中上尾相依系數和下尾相依系數總是相等的。在現實數據中，兩個變量的上尾相依系數和下尾相依系數并不總是相等的。另外，當所包含的變量數量不斷增加的時候，此模型描述尾部相依關系的能力將會降低。當然，通過本文的闡述和對實際數據估測，時變T-Copula 模型可以足夠好地描述多種合約的條件相關系數和在一定程度上體現數據中的顯著的尾部相依關系。

注釋：

①數據來源于上海期貨交易所網站。

②每個交易品種的合約信息可以在上海期貨交易所網站獲得，http：//www.shfe.com.cn/。

③在目前中國期貨市場的高頻數據中，我們可以引入不少外生變量，比如成交量、持倉量、買量和賣量等。

④在實際估測中，對于杠桿項不顯著的合約，可以用GARCH（1，1）模型替換GJR（1，1）模型。在本文中，仍然用GRJ（1，1）并且相信對模型的估測不會有很大影響。

⑤T-Copula 模型的相關系數矩陣在數值上很接近，但一般情況下不等于各個合約價格變化的相關系數矩陣。