課堂教學優化與減輕學生課業負擔的關系

岳東旭

摘要：在課堂教學中使學生掌握教學內容，在校期間基本做完作業，做到在不加重學生學習負擔的前提下，不斷提高數學教學質量。筆者以“勾股定理教學中難點的突破方法探究”為例，通過合理設置課程，從轉變教學觀念，提高教學效率等幾個方面進行闡述。讓學生參與獲得知識的過程，學會學習新知識的方法，提升學生的自學能力。提高教學效率，真正達到減輕學生負擔的目的。

關鍵詞：減負;勾股定理;直角三角形;探究活動;重要基礎

中圖分類號：G633.6 ??文獻標識碼：A ??文章編號：1992-7711（2019）10-0109

一、優化課堂教學減輕學生課業負擔

1. 課程設置合理。上足課時，把課堂時間還給學生，不額外加課，保障學生有充足的休息和調整時間，課間有時間為下一節課做好準備。

2. 轉變課堂教學觀念。現代的課堂教學效率觀認為生活中隨處是課堂，隨時是教學，時時處處學知識。每一位教師都要增強效率觀念，強化效率意識，提高課堂40分鐘的教學效率。

3. 提高課堂效率。（1）未雨綢繆，強化課前準備。學生汲取知識的開端是課前準備，課堂效率的高低受課前準備的影響，特別是數學課，提高課堂效率，學生的課前預習和準備必須到位。（2）抓住主題，保障課堂教學。要讓學生在有限的時間內掌握新知識，教師就要改變教學觀念，主次分明，抓住主要問題，突出重點、攻克難點。首先，教學環節上，要圍繞新知識展開。每個教學環節都要以新知識為中心，為學生獲取新知識服務。其次，教學過程要重點突出。找到新舊知識之間的聯系，抓住學生知識的生長點進行教學。人民教育出版社義務教育教科書八年級數學在編寫的過程中雖然注意到了學生接受知識需要經歷感知、理解、鞏固、應用的過程，設計中重視學生動手能力的培養。然而，教材設計過程中并未給出教學難點突破的方法。

二、在實際教學中引導學生順利突破思維難點

1. 證明勾股定理——拼圖

雖然勾股定理的證明方法迄今為止已逾500種，但讓學生很自然地想到證明方法是很困難的，特別是學生如何想到用四個全等的直角三角形拼成正方形，利用“等積法”證明。

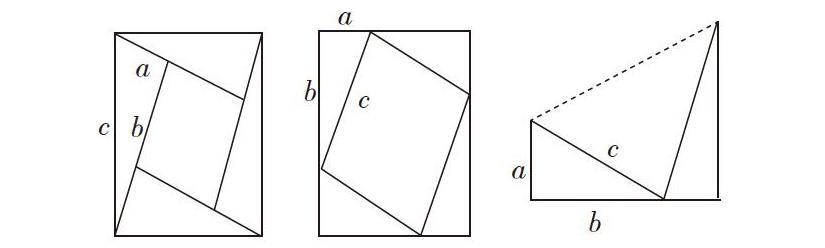
情景再現：利用手中的四個全等的直角三角形拼圖證明勾股定理

[c][a][b][a][b][c] [c][a][b]

設計意圖：用拼圖法驗證勾股定理是以數形轉換為指導，圖形的拼補為手段，以各（部分）的面積和等于（整體）的面積為依據來達到目的。旨在讓學生親自動手，在拼圖驗證的過程中，體驗數形結合等數學思想方法，獲取獲得知識的方法手段的能力。

然而，實際的教學中會發現學生很難在有限的課堂時間內想到如何拼圖，思維上存在著以下障礙。

思維障礙：（1）為何要用拼圖證明？（2）為何要用直角三角形拼圖？（3）拼成什么樣的圖形？

有效的課堂教學要建立在學生已有的知識和能力基礎之上，教師要善于合理設置問題引導學生進行有效的思考，激發學生的學習興趣，幫助學生快速突破思維障礙。

突破方法：

①引導學生思考勾股定理表達式，對于等式的證明一般采取從一側證向另一側，或者是兩側向中間證明的方式。然而，對于本式兩側都是簡單的形式，不能再化簡，另一方面引導學生思考勾股定理本身是從“形”到“數”的一個過程，以及學生在學習完全平方公式時，曾用過幾何圖形驗證過完全平方公式的正確性。若在教學中能在這里引導學生思考，則學生很自然可以想到利用幾何圖形證明勾股定理。從而解釋了學生心中所產生的第一個疑惑，順利突破第一層次的思維障礙。

②引導學生回顧勾股定理的發現過程。它揭示的是直角三角形三邊之間的數量關系。因此在證明過程中自然要用直角三角形作為基本構圖素材。

③引導學生觀察勾股定理表達式本身的特點，再結合回顧勾股定理的發現過程，學生不難發現式子本身符合正方形的面積公式。因此拼成正方形有利于證明定理。教師進一步引導，既然拼成正方形，那么對所需要的直角三角形有什么樣的要求？比如需要幾個，比如幾個三角形是否需要全等。

2. “選數畫圖”——猜想

數學的學習常常要經歷從特殊到一般的過程，經歷觀察、猜想、歸納、驗證、應用的獲取知識的過程。這符合初中學生身心發展的一般規律。但在實際教學中不能為了使學生經歷這樣的過程而設置一些假設性的無效探究。

情景再現：畫畫看，寫出幾組三角形三邊長，并探究它們之間滿足的數量關系，畫出這些三角形，量量看它們是否是直角三角形。

設計意圖：勾股定理的逆定理的證明是一種以計算方式證明幾何問題的方法，學生對于這種利用計算證明幾何結論比較陌生。教材中設計這個環節一是想通過這樣的方式猜想出結論，另外也是對這種證明方式的引導。但實際的教學中會發現學生動手操作的目的性并不明確，探究的方向也不明確，實際教學過程大打折扣。

思維障礙：

（1）選哪些數？（2）數量之間的關系有多種。（3）畫圖存在誤差。

教學建議：

基于以上三個問題，教材中所呈現的活動不具有可操作性，即便是讓學生動手操作也是一種假探究，因此在實際教學過程中直接刪去。直接從學生已有的學習幾何圖形性質定理與判定定理的關系入手，猜想出逆定理，然后再思考如何進行證明的問題，把教學的重心放在證明方法的探究上。

3. 證明勾股定理逆定理——構圖

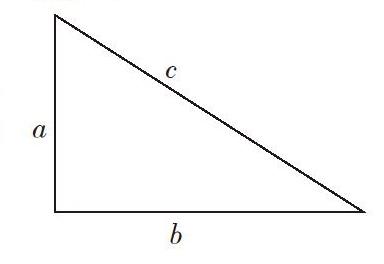
情景再現：證明命題2 如果△ABC的三邊長a，b，c滿足a2+b2=c2，那么這個三角形是直角三角形。

[a][b][c][如圖，若三角形三邊長為a，b，b且a2+b2=c2，則三角形是直角三角形]

思維障礙及突破方法：

本環節教材中給出的證明方法是：先畫兩條直角邊分別為a，b的直角三角形，如果△ABC與這個直角三角形全等，那么△ABC就是一個直角三角形。這里如果教材不直接給出思路，學生很難想得到。

在實際的教學過程中，教師要引導學生思考所用方法的必然性和合理性。一方面引導學生回顧所掌握的直角三角形的證明方法，進而繼續分析問題中給出的條件發現，我們根本無法直接證明兩角互余或者有一個角是90°，那么我們只有第三種方法可用，即證明其中一個角和已知的直角相等。因此必須先構造直角，且還方便證明相等。這樣，學生容易想到剛學過的三角形全等知識。

4. 精選課后作業

事實證明，做的練習題的多少與學習成績好壞并不成正比，若學生內心反感，無論做多少練習題都無效。作業中是機械重復的知識會使學生失去興趣。教師需要精心設計和選擇作業，做到精益求精，提高學生的作業質量。

5. 注重教后反思

課堂教學結束后，要從各個方面反思自己的教學過程是否有效，在以后的教學中打算如何改進。

總之，作為一名教師，要設法提高學生的學習效率，使學生樂于面對課業任務，學習上有的放矢，精益求精，做到“減負不減效”，讓學校的教學質量在“輕松無壓力、快樂我要學”的佳境中創造輝煌。

參考文獻：

[1] [美]邁克爾·塞拉，李翼忠，劉仁蘇，蔡上鶴等.發現幾何：一種歸納的方法[M].北京：人民教育出版社，2000.

[2] 朱 哲，張維忠.從趙爽弦圖證明談數學史教學應尊重歷史[J].中學數學月刊，2005（10）.