品形數之美悟數形之妙
——《數與形》教學設計與反思

屈 婷 袁凌云

【教學內容】

人教版六年級上冊第107頁例1。

【教學過程】

一、數與形，各展其長

1.男生女生大PK：第一組題展示給男生，第二組展示給女生，展示后分別計算答題時間定輸贏。

第二組：如下圖，甲數和乙數相比，（ ）大。

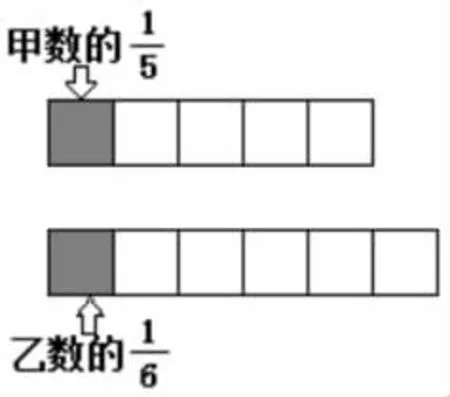
師：同樣的題目，為什么女生用時這么少？

小結：雖然問題相同，但給出圖形的題目一眼就能看出結果。

2.第二輪PK：

（1）這個角是（ ）角。

（2）一個角的度數是 89°，這個角是（ ）角。

師：這次給女生的題目是數，給男生的是圖形，為什么男生又輸了？

小結：給出的圖形需要測量，給出的角的度數有數據，方便判斷角的類型。

師：看來圖形和數據都有優點，也有缺點。華羅庚說過：數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休。數形結合到底有哪些好處呢？今天這節課我們就來研究。

【設計意圖：在小學階段，很多數學知識都是在數形結合的基礎上逐步抽象概括的，數形結合的思想一直伴隨在學生的身邊，只是沒向學生特別點明。數與形是數學知識的兩種不同表征形式，沒有高低之分、優劣之說。如何讓學生體會數抽象、形直觀的特點？筆者為學生提供了兩個例子，一是為了喚醒學生對數與形的認識，感受數與形的一路相伴。二是便于讓學生初步體會到數與形各有優勢：有時數可以助形，利用數的精確能夠準確量化形的特征；有時形可以幫數，借助形的直觀可以降低數量關系的抽象程度。】

二、圖與式，相輔相成

師：如果用一個□表示1，1+3可以怎樣畫圖？1、3分別在圖中的哪里？怎樣讓別人一眼看出1、3在圖中的哪個位置？（用不同顏色加以區分）

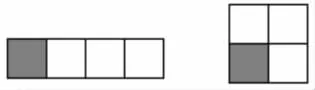
師：一共有多少個小正方形？你是怎么知道的？

板書：1+3 2×2 （4個）

小結：用加法和乘法都可以計算小正方形的個數。

師：1+3+5可以怎樣畫？畫出的圖形哪種便于計算？為什么？

小結：畫成長方形或不規則圖形要一個一個地數，畫成正方形更容易用3×3計算結果。

板書：1+3+5 3×3 （9個）

師：同一個正方形，為什么既可以寫成兩個數相乘的形式，又可以寫成幾個數連加的形式？這些等式，我們是借助什么得到的？

【設計意圖：要實現數形結合，首先要完成數與形的轉化。“從1開始的連續奇數相加的算式對應的圖不只一種，為什么要研究拼成正方形的形？”這是學生的疑惑之處。因此筆者首先出示“1+3”的算式，讓學生構造形，體會形雖然有多種，但數字和圖卻是一一對應的。接著讓學生畫出“1+3+5”對應的形，從“多樣化的形”到“呈正方形的形”，旨在讓學生體會“形”有繁簡之分，正方形方格具有明顯的圖形特征，便于用乘法計算出“1+3+5”的結果。最后，讓學生感悟到同樣的圖形換個角度看，可以產生不同的算法，用兩種不同的方式計算同一個幾何量，就可以得到一個等式。這樣就將數與形進行了溝通與轉化，讓學生體會到數形之間的密切聯系。】

三、想與畫，虛實相生

師：按照這樣的規律，如果再增加一個加數，你認為是多少？（加7）先想一想，這個算式等于哪兩個數相乘，它所對應的正方形邊長是多少？再畫一畫，驗證你的猜想是否正確。

師：為什么1+3+5+7還可以寫成4×4相乘？除了用圖形來解釋，這兩個算式之間是否也存在內在聯系？1+3+5+7這個算式中是否也藏著4？你能找到嗎？4在正方形圖中是什么意思？

師：結合前面的算式和圖看一看，是否也存在這樣的規律？這些加數隨便是幾都可以嗎？剛才說增加加數的時候，你們怎么異口同聲說要加7？3+5+7可以寫成3×3嗎？

師：像 1、4、9、16 這些數都可以用一個實心的正方形來表示，這些數是一些和形狀有關的數，數學家把它叫做正方形數。1是不是平方數？符合這個規律嗎？

師：邊長是6的正方形可以轉化成哪些算式？如果分割成從1開始的連續奇數相加，加數可能是哪幾個？

【設計意圖：對于此類問題，不管是數還是形，都有規律可循。規律探尋雖然不是本節課的主旋律，但發現規律的過程能逼著學生把數與形統一起來觀察與思考。在這一環節中，筆者讓學生先猜想“1+3+5之后接下來該加哪個數”，想象之后再畫圖，讓學生在頭腦中先定格圖形，再通過畫圖幫助學生確定想象的圖形是否正確，為推算“從1開始的連續奇數連加的結果與平方數之間的關系”打下根基；接著，引導學生發現等式左邊加數的個數、等式右邊的相同因數與正方形邊長的對應關系；最后，把學生的目光聚焦到加數的特點上，明確只有從1開始的連續奇數相加才符合這個規律。在這一過程中，學生利用想象形成的表象，聯系畫圖過程回想，自發將數與圖聯系起來思考，在整體上把握數與形的對應關系，將數與形結合起來發現規律。】

【教學思考】

一、圖式互譯，數形轉換，架設思維通道

在學生的認知結構中數是數，形是形，難以統一。將數的問題轉化成形的問題，從形中尋找計算方法，通過數形的轉換，能讓學生體會到數與形都是表征問題的方式，由此打通形象思維與抽象思維之間的數學通道。因此，筆者從式引入，給出算式讓學生用圖形來表征，以形表數，這樣就將數的問題轉化成形的問題。當學生用直觀的圖形表征算式之后，讓學生指出這些連續奇數分別在圖中的什么位置，數形對照，算式與圖形一一對應，培養學生尋找數與形對應的能力。如果說“由數想形”是順向思維的話，那么“見形思數”就是逆向思維。當學生尋找到等式與正方形方格圖的規律之后，筆者引導學生思考“邊長是6的正方形方格圖可以轉化成哪些算式？如果分割成從1開始的連續奇數相加，可能是哪幾個”，讓學生在頭腦中對正方形方格進行分拆與計算，與“式”建立聯系，經歷從圖形到算式的回流，培養學生的數形轉換能力。

二、內聯溝通，數形結合，搭建思維橋梁

圖形直觀、形象的特點，決定了化數為形能夠達到以簡馭繁的目的。因此，筆者以直觀的正方形方格為載體，引導學生將算式與圖形結合起來觀察、思考，以形解數，尋找加法算式的簡便算法。等式的左右兩邊，落實到圖形中，都是對小正方形個數（或大正方面積）的計算。對一個圖形，從不同的角度研究它、計算它，能得到一個等式。“從1開始的連續奇數相加可以用同數相乘來計算，奇數的個數、形態與相乘的因數有怎樣的關系，又與正方形的邊長有怎樣的聯系？”這幾個問題讓學生在反觀數與形的關系進而發現規律的過程中，漸漸體會到：規律如果沒有直觀圖形作思考的載體，很難被發現和理解；只通過圖形，不借助算式也難以建立正方形數與算式之間的聯系。形之于數解釋現象的作用逐步發揮出來，數之于形發現規律的價值慢慢被彰顯，形數的特點深深印在學生的腦海中。

三、抽絲剝繭，數形互助，打通思維血脈

就數學本質而言，“從1開始的連續奇數相加”可以利用等差數列求和公式“（首項+末項）×項數÷2”來計算。由于這個數列的特殊性，（首項+末項）÷2得到的結果正好與項數（奇數的個數）相等，而奇數的個數正好等于正方形的邊長，因此可以寫成同數相乘的形式。小學生沒有學過數列，難以領略到其中的數學本質，但等差數列的結構特征與構成正方形“L”形的結構特征是有內在聯系的。如何通過數形結合的方法讓學生逐步體悟正方形數的魅力？當學生探究出規律后，我再次引領學生把算式與圖聯系起來思考，深究現象背后的道理，讓學生進一步感悟到數的結構特征與形的結構特征高度一致，感悟數形之間的密切聯系。