載荷自適應五連桿抽油機的算法實現

向新勝，貢軍民，劉牧洲 (中石油新疆石油管理局工程技術公司，新疆 克拉瑪依 834000)

郭登明，代慧 (長江大學機械工程學院，湖北 荊州 434023)

楊建忠 (中石油渤海石油裝備制造有限公司遼河熱采機械制造分公司，遼寧 盤錦 124209)

李學清 (中石化西南石油工程有限公司裝備管理處，四川 成都 610041)

隨著油田進入中后期開發階段，原油含水率不斷上升,油層壓力降低,油井動液面逐漸下降,為了保持原油穩產，降低采油成本，要求采油設備不僅能滿足“深抽、大排量”提液的工藝要求，而且要具有能耗低、可靠性高等特點，文獻[1]介紹了一種新型載荷自適應五連桿節能抽油機的設計方法和性能特點。該抽油機的計算方法比較復雜，下面筆者介紹載荷自適應五連桿抽油機詳細算法，供有關設計者和使用者參考。

1 載荷自適應五連桿抽油機

載荷自適應五連桿抽油機簡圖如圖1所示，游梁平衡重W1與副連桿BC連成一體，分別與游梁、主連桿(BA)鉸接。該抽油機是曲柄1、連桿2、副連桿3、游梁5及機架組成。按照平面機構理論，該抽油機機構由2個自由度構成，必須有2個驅動件才能使機構有確定的運動。但是，由于游梁平衡重W1與懸點總載荷W′的相互作用、相互適應，其結果是當曲柄在任何位置時，使得游梁具有確定的位置。即當游梁平衡重W1和懸點靜載荷W2一定時，游梁擺角δ隨曲柄轉角θ而定，可歸屬于單自由度問題，只是計算方法比較復雜而已，故該抽油機實際上是一種載荷自適應型五連桿單自由度抽油機。

2 受力分析

幾何計算、運動分析在文獻[1]已有詳細有推導，受力計算也簡單的介紹，這里只對機構的受力分析和滿足機構運動存在的條件進行介紹。假定該抽油機各個運動構件的長度為已知，曲柄作勻速轉動，以曲柄轉角θ和游梁擺角δ為驅動變量(二自由度)，則可按照五連桿機構的計算方法進行幾何計算、運動計算。這里略去幾何計算、運動分析，只進行受力分析計算[2，3]。

注：W1為游梁平衡重，N；WK為游梁平衡重產生的慣性力，N；W′為懸點總載荷，N；FL為連桿力,N；θ為曲柄轉角，(°)；δ為游梁擺角，(°)；α為曲柄與連桿夾角，(°)；β為連桿與副連桿夾角，(°)； α1為副連桿與副平衡臂夾角，(°)；β1為副連桿與游梁后臂夾角，(°)；ω為曲柄角速度，rad/s。圖1 載荷自適應五連桿抽油機簡圖和受力簡圖

懸點總載荷為：

(1)

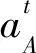
以C點列力平衡方程：

F3=W1+FL·sin(β-β1-δ)

F4=FL·cos(β-β1-δ)

(2)

式中：FL為連桿力，N；F3為C點的垂直分力，N；F4為C點的水平分力，N。

若不計游梁平衡重的慣性載荷，取游梁支座為研究對象，列力平衡方程：

FX=-F4

FY=F3+W′

(3)

F3·c·cosδ+F4·c·sinδ=W′·a

c·cosδ·W1+FL·c·sin(β-β1)=W′·a

(4)

解之得：

(5)

式中：FX、FY為軸承座力，N；a為游梁前臂長度，m；c為游梁后臂長度，m。

在整個抽油機受力分析過程中，必須滿足如下條件：

(6)

式中：d為副平衡臂長度，m，b為副連桿長度，m。

3 數值求解算法

3.1 確定驢頭上下沖程的死點

在理論分析中，只有滿足式(6)的解才是正確的。為此，先求出在靜載荷作用下，滿足式(6)的游梁擺角δ和曲柄轉角θ之間的函數關系；從而求出游梁擺角δ(與曲柄轉角對應的離散值)。根據δ值變化區間確定抽油機的上下死點：當δ值由增加趨勢變為減小的趨勢時，此時δmax值為驢頭下死點；反過來，當δ值由減小趨勢變為增加趨勢時，此時δmin值為驢頭上死點。這樣，將游梁擺角δ的值分為上沖程區域和下沖程區域，用該方法確定的驢頭上下死點比較準確，只是曲柄轉角θ的變化值不能太大，一般控制在0.5～1°為宜。

3.2 速度和加速度的算法

前面已經計算出靜載荷下滿足力矩平衡公式(6)的游梁擺角δ(離散值)，對角位移求一階導數可以得到角速度，對角位移求二階導數可以求出角加速度。由于游梁的角位移是一些離散的點，求解其角速度和角加速度不能直接采用常規求導法。對離散的點求解導數方法應當采用數值微分[4,5]。

通常，一階數值微分的三點公式如下:

(7)

(8)

式(7)與式(8)的區別在于：①式(7)是端點逼近公式，當h<0表示從左端點逼近，h>0表示從右端點逼近，而式(8)是中點公式；②雖然誤差都是O(h2)，但式(8)的誤差約為式(7)的一半；③式(7)僅使用了x0單側(左側或右側)的數據，式(8)使用了x0兩側的數據。

一階數值微分的五點公式如下：

(9)

對游梁擺角δ求解二階導數可以求得其角加速度，進而求出懸點的加速度。同樣，二階導數也存在二階微分三點公式和五點公式。

二階微分三點公式如下：

(10)

(11)

式(10)為中點公式，式(11)為端點逼近公式，當h<0表示從右端點逼近，h>0表示從左端點逼近。

二階微分五點公式如下：

(12)

在實際計算過程中，為了提高計算精度，如果某一區域的計算點多于5個，則使用5點微分中點公式進行計算；如果某一區域的計算點多于3個，則使用3點微分中點公式進行計算；其他計算點則使用三點公式中的端點逼近公式進行計算。

3.3 迭代方法及收斂性分析

3.3.1 迭代方法分析

在計算游梁擺角δ和平衡扭矩MB時，要求有一種合理、快速的計算方法，否則既不能滿足精度要求，也影響計算速度，甚至出現計算死循環的情況。在優化設計過程中，針對不同的情況有很多算法，這里采用對分法進行求解。在求解游梁擺角δ時，在確定曲柄轉角的前提下，以副連桿與主連桿成一條直線確定最大的游梁擺角δmax1；以副連桿與游梁后臂重合確定最小的游梁擺角δmin1，不管怎么變化，游梁的實際擺角一定在δmax1～δmin1之間，只要給出相應的迭代誤差值ε，采用對分法很快可以求出滿足式(2)的計算游梁擺角δ，且收斂速度快，精度高。在求解平衡扭矩MB時，參照四連桿機構抽油機的計算方法，先初步估算一個最大的平衡扭矩MB max1和一個最小的平衡扭矩MB min1，同樣用對分法，給出一個迭代誤差ε，可以計算出平衡扭矩MB，且收斂速度快，精度高[6]。

3.3.2 迭代收斂性分析

圖2 迭代計算框圖

在計算游梁擺角δ和平衡扭矩MB時，都存在一個迭代收斂的問題，從理論分析可以知道，這2種迭代過程都是單向收斂的。另外，在考慮動載荷以后，原來的最大靜載荷就變成了最大懸點載荷，再通過考慮加速度的影響，計算得出實際靜載荷。那么，其他各個位置的載荷就是靜載荷+動載荷。這樣，在重新計算游梁擺角δ、懸點速度、懸點加速度等參數時，就存在收斂性的問題，為此，筆者將計算結果與前一次的計算結果進行對比，主要是進行曲柄在一個運轉周期內，將靜載荷下和動載荷下得到的游梁擺角、速度、加速度制成數據曲線圖進行對照，其重合度必須滿足設定要求，直到收斂為止。

總的思路如下:①先求出在靜載荷作用下，滿足式(6)的游梁擺角δ和曲柄轉角θ之間的函數關系；從而求出游梁擺角δ(與曲柄轉角對應的離散值)；②運用數值微分方法[7，8]，求出游梁擺角δ的一階導數和二階導數(即角速度和角加速度)，從而求出其他各點在不同位置的速度和加速度；③考慮動載荷，重新計算游梁擺角δ和曲柄轉角θ之間的函數關系，再進行速度計算、加速度計算、受力計算、平衡計算，直到滿足收斂要求為止。整個程序流程的框圖如圖2所示。

在數值微分時為了減少誤差，應當采用五點插值公式中的中點公式[5]，其截斷誤差為O(h4)，當接近邊界時，應用三點插值公式中的中點計算公式[6],其截斷誤差為O(h2),只是在邊界處不能使用中點公式計算時，計算結果仍有些誤差，這稱為數值計算過程中的“吉布斯”現象，可能造成局部點的誤差，但不影響整個計算結果。

4 計算實例及分析

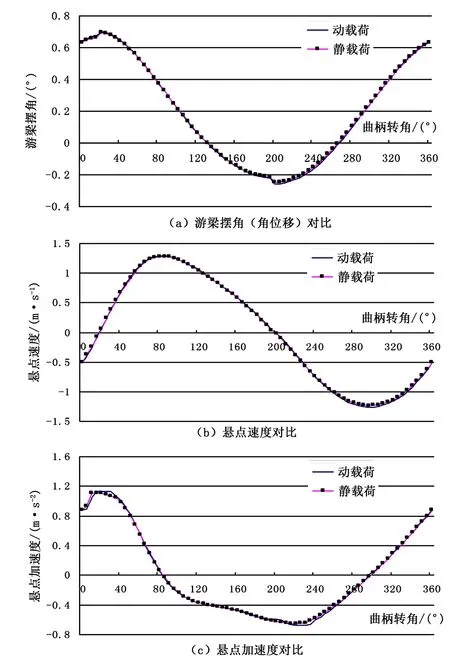
圖3 靜、動載荷下懸點角位移、速度、加速度的對比

以CYJZ10-4.2-53HF型抽油機為例，研究自適應五連桿抽油機的性能特點。抽油機機構尺寸如下：曲柄半徑(R)為1120mm；連桿長度(P)為3800mm；游梁后臂長度(C)為2550mm；游梁前臂長度(A)為4365mm；減速器輸出軸中心到支架軸承中心的水平距離(I)為3400mm；減速器輸出軸中心到支架軸承中心的垂直距離(H-G)為3615mm；副連桿(BC)長度(B)為855mm。計算工況為沖次數(n)為6.0min-1；泵徑(d)為44mm，理論計算沖程(S)為4.20m。圖3為靜、動載荷下懸點角位移、速度、加速度的對比。從圖3可以看出，考慮動載荷以后，與靜載荷的計算結果較為相符，說明迭代是收斂[9]。

5 結論

1)載荷自適應五連桿抽油機的具體算法雖然比較復雜，但經過劃分區域、離散化以后，運用數值微分中的三點和五點插值公式可以方便地計算出自適應五連機構的幾何參數、運動參數，且計速度快、精度較高；為進一步的工藝計算、動力計算、平衡計算和功率計算提供必要的數據。

2)在未知動載荷的條件下，運用靜載計算自適應五連機構的幾何參數、運動參數；再考慮動載荷的影響，重新計算自適應五連機構的幾何參數、運動參數，這種逐步搜索的計算方法是可行的，且計算結果是收斂的。

3)該數值計算方法為其他同類型的二自由度自適應抽油機的設計計算提供了有效的技術支撐。