基于GM(1,1)回歸模型的煙臺市物流需求預測
卜令營,侯 宏,樊東鑫
(煙臺大學 經濟管理學院,山東 煙臺 264005)
1 引言
物流業作為社會經濟發展的新生產業,逐漸受到政府和社會的廣泛關注。一般來說,一個地區的物流水平在某種程度上體現了該地區的經濟發展水平和社會管理水平。物流是城市經濟發展的基礎,是連通生產和消費之間的橋梁,更是衡量一個國家綜合國力和現代化水平的主要標志之一。根據供需平衡理論,當物流服務的供給小于其需求時,會在一定程度上抑制物流需求,造成需求不足;同理,如果供給大于需求,則會產生資源閑置,造成資源浪費,進而降低物流效率,所以準確而合理的物流需求預測顯得尤為重要。
物流需求預測就是根據過去的資料和數據,運用一定的手段和方法,對未來的物流需求進行準確的分析和估計,其目的在于指導和管理物流活動,調整產業結構,優化資源利用,從而制定物流發展政策和規劃。
煙臺地理位置優越,面向日韓及東北亞經濟發達地區,背靠京津魯豫廣闊的經濟腹地,擁有鐵路、公路、水路和管道“四位一體”的集疏運網絡;同時具備較好的產業基礎和政策環境支持,現已初步建立起化工、電子、建材、煤炭等門類齊全的產業生產體系,是山東省重要的工業生產基地;煙臺作為山東新舊動能轉換、中韓(煙臺)產業園、“一帶一路”海上重要節點城市以及山東自貿區煙臺片區四個國家戰略于一身,政策疊加效應凸顯。本文正是在這一背景和前提下,對煙臺市物流發展現狀及發展目標進行分析,構建準確的預測模型,對物流需求進行合理分析,從而制定城市物流發展規劃,進一步將煙臺市打造成東北亞物流交通樞紐。
2 文獻綜述
隨著經濟的快速發展,有關物流需求預測方面的研究也越來越多。目前,學者們對物流需求的預測方法可大體歸納為三大類:一為定性預測方法,如德爾菲法、情景分析法、集體意見法等,該方法在數據缺乏時比較適用,方法較簡單,主觀因素較大,預測精度不高,很少有學者使用。其二為定量預測方法,即根據一定的歷史數據,運用相關方法,構建合理的數學模型,對預測對象的未來狀態和性質進行估計推斷,如灰色預測模型、線性回歸法(包括一元和多元)、時間序列預測法等,該方法適用于數據較多且要求較高的精確度,例如周曉娟,景志英[1]建立多元線性回歸模型,對河北省的物流需求進行預測,并提出了加快河北省物流發展的建議;張麗萍等[2]利用灰色模型GM(1,1)對臨沂市物流進行預測;邱慧等[3]利用灰色預測模型GM(1,2)模型,對山西省未來三年的物流需求進行了較高精度的預測;李凱,張濤[4]基于改進的GM(1,1)模型對上海市2017—2020 年的GDP 進行了預測;黃毅,夏國恩[5]基于SVR 模型對廣西省的物流需求進行了預測。其三為組合預測方法,即利用多種預測方法進行組合后預測。如徐興華[4]基于經濟學的視角分析物流需求影響,采用組合預測方法進行了物流需求預測研究;楊樹果,王新利[5]將偏最小二乘回歸與灰色模型耦合對物流需求進行預測,充分利用了兩者的優點,使預測精度進一步提高,預測結果更加合理;劉文慧,王少然[6]建立了基于GM(1,1)回歸的預測模型,并預測了未來十年天津市農產品產量預測值,表明多元線性回歸結合GM(1,1)模型可以用來做預測。
以往學者大都采用單一的灰色系統模型對物流需求進行預測,精確度不高,較少采用組合預測方法,尤其是較少采用基于GM(1,1)回歸的預測模型對物流需求進行預測。物流需求量受到多個經濟因素的共同影響,多元線性回歸模型可以綜合考慮影響貨運量的因素,而且根據回歸分析,消除了變量間的多重共線性和自相關性。以解釋變量的GM(1,1)預測值為基礎對多元線性回歸模型中的被解釋變量進行預測,所得預測結果將具有說服力;將被解釋變量的灰色預測結果與基于GM(1,1)回歸模型的結果相互對比,進一步證實了組合預測方法的精確度與合理性。
本文根據煙臺市的實際發展情況,選取統計年鑒中1998-2017 年影響貨運量的相關因素作為預測模型的解釋變量,采用組合預測方法進行預測,建立基于GM(1,1)回歸的需求預測模型對煙臺市未來五年的貨運量進行了預測,并與多元線性回歸的結果進行比較,結果表明,基于GM(1,1)的多元線性回歸模型具有較高的預測精度,為煙臺市物流資源的合理配置、產業結構優化升級以及為政府制定現代物流業的發展規劃提供了參考。
3 數據選取及描述性統計
影響物流需求的因素很多,有經濟因素,也有非經濟因素,而且各因素之間具有較強的相關性,在借鑒以往學者研究的基礎上,結合煙臺市物流發展現狀以及充分考慮所選指標的易獲取性、科學性、全面性等原則,本文主要選取了煙臺市貨運量Y(萬t)作為被解釋變量,第一產業產值X1(億元),第二產業產值X2(億元),第三產業產值X3(億元),固定資產投資X4(億元),社會消費品零售額X5(億元),外貿進出口總額X6(億美元),公路通車里程X7(km),沿海貨物吞吐量X8(萬t)八個指標作為解釋變量(見表1)。選擇第一二三產業產值取代地區生產總值作為解釋變量,是因為一方面它可以解釋產業結構對物流需求的影響,另一方面也可以解釋地區生產總值對物流的影響。
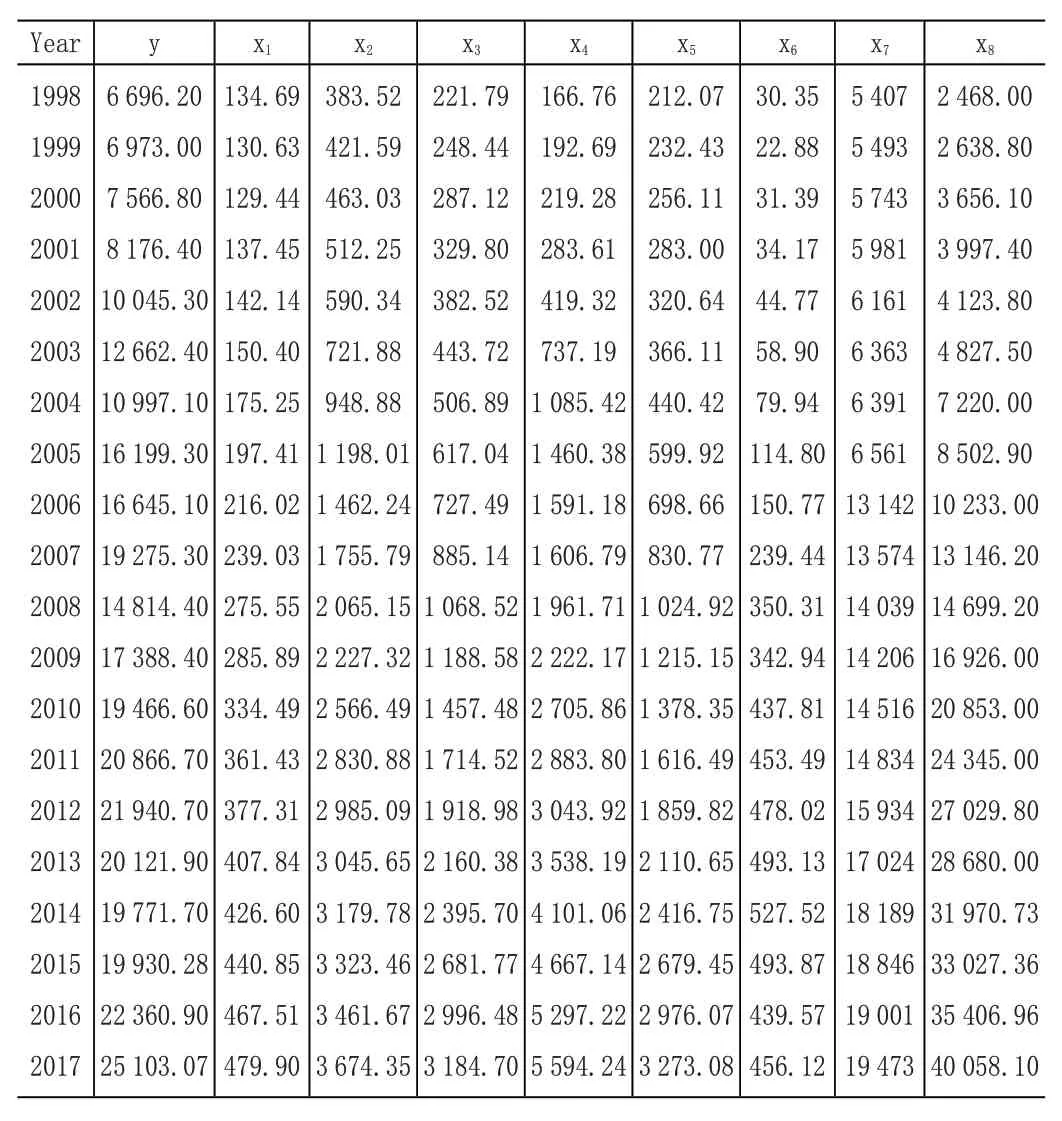
表1 煙臺市1998-2018年相關影響因素指標數據
4 實證分析
4.1 建立多元線性回歸模型
多元線性回歸模型的一般形式為Y=β0+β1X1+β2X2+...+βpXp+ε,其中β0,β1,β2,…,βp是有待回歸確定的系數,y是被解釋變量,X1,X2,…,Xp是解釋變量,ε是隨機誤差。根據表1相關影響指標可建立煙臺市物流需求模型:
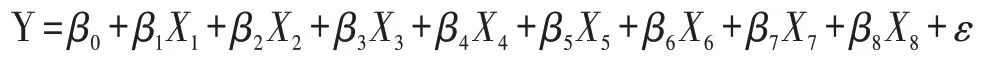
4.2 相關性分析
通常認為,當兩變量相關系數之間的絕對值大于0.8時,具有較強的線性關系,而相關系數的絕對值小于0.3時,則表明兩變量之間的線性關系較弱。
由表2可以看出,解釋變量之間的相關系數非常高,均大于0.8,而且均在0.05 水平顯著,懷疑存在嚴重的多重共線性。一般來說,解釋變量之間的相關性是普遍存在的,在一定程度上也是允許的。
4.3 參數估計
將表1中相關影響因素指標數據導入Stata15 軟件,運用普通最小二乘法估計,得到回歸結果見表3。

表2 解釋變量的相關系數矩陣
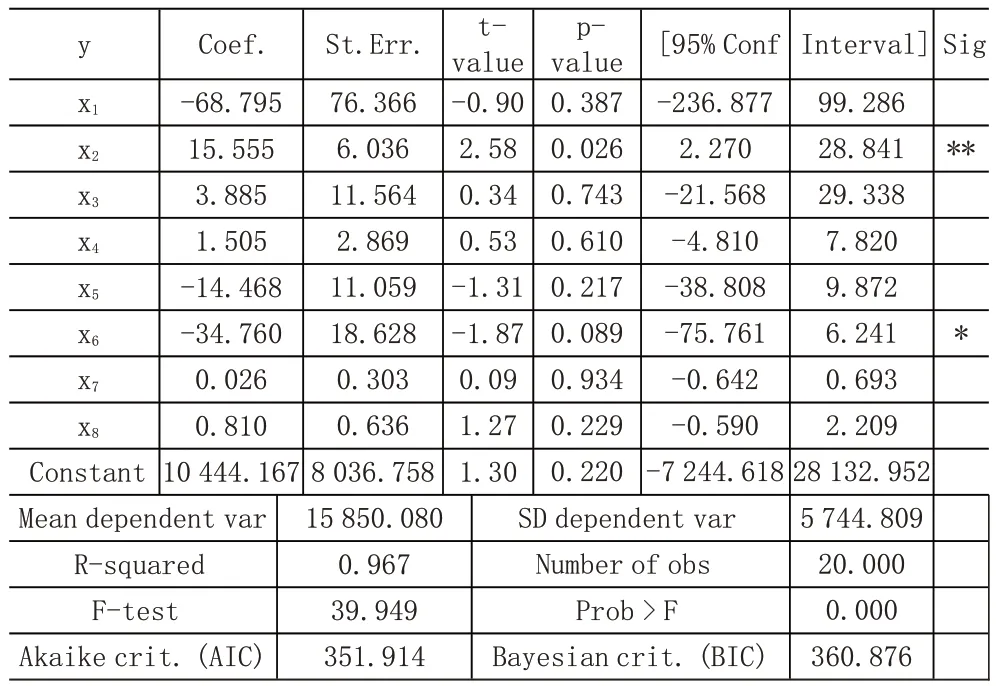
表3 最小二乘法參數估計結果
4.4 模型檢驗
4.4.1 多重共線性檢驗及修正。從回歸結果可以看出:y對8個自變量的線性回歸方程為:y=10 444.167-68.795X1+15.555X2+3.885X3+1.505X44-14.468X5-34.760X6+0.026X7+0.810X8,可決系數R2=0.967表明回歸方程的擬合程度很高,F=39.949,P=0.000<0.05可知回歸方程拒絕零假設,通過了F檢驗,說明變量X1,X2,X3,X4,X5,X6,X7,X8整體上對y有高度顯著的線性影響。
但是自變量回歸系數只有X2,X6顯著,其它系數均不顯著,進一步確定存在嚴重的多重共線性。多重共線性普遍存在,其所表現的是一個程度大小的問題。對于多重共線性的修正方法,一般有逐步回歸法、主成分分析法、嶺回歸等,本文選擇用逐步回歸法來降低多重共線性的嚴重程度。
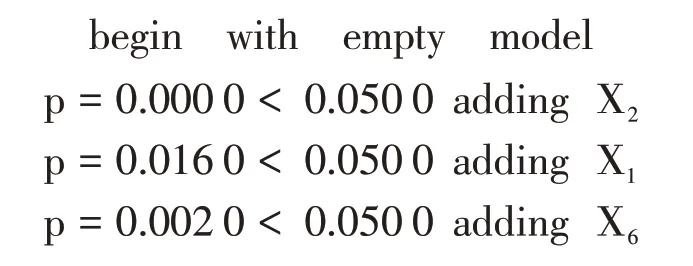
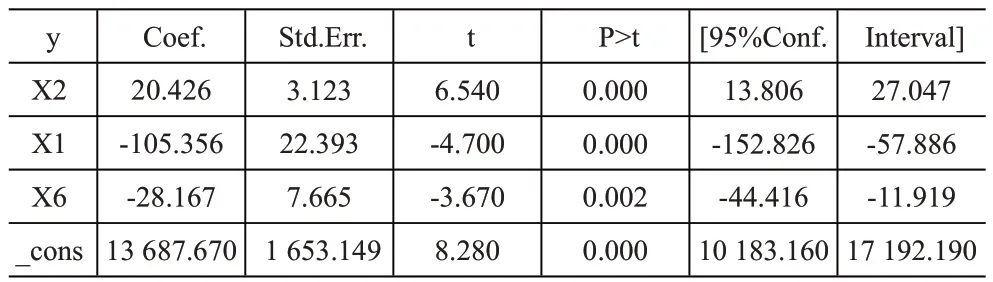
表4 逐步回歸法結果顯示
經逐步回歸得到新的線性回歸模型為y=13 687.670-105.356X1+20.426X2-28.167X6,R^2=0.955 0 ,Pr ob >F=0.000 0,方程通過了F檢驗,而且各變量的系數顯著,多重共線性程度被削弱。
4.4.2 自相關檢驗。結果顯示d=2.185 972,對于n=20,k=4,在 5%的顯著水平查表得 d1=0.894 ,d2=1.828 ,du≤d ≤4-dl,無法判斷是否存在自相關,DW檢驗失效,改用BG檢驗。

表5 BG檢驗
由 BG 檢驗可知,p 值為 0.670 大于 0.05,故接受原假設H0,即不存在自相關。
4.4.3 異方差性檢驗。本文采用懷特檢驗來檢驗是否存在異方差,結果見表6。
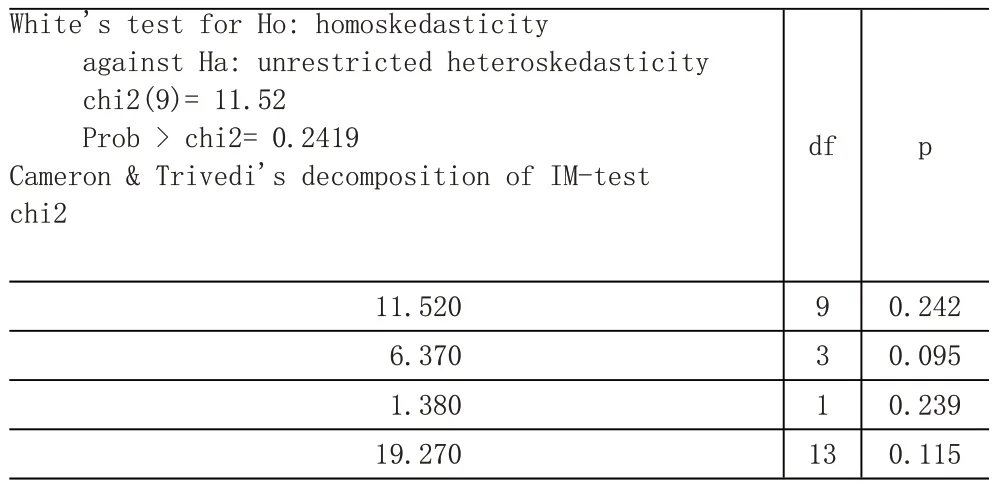
表6 懷特檢驗
由表6中數據可知,p值均大于0.05,沒有通過顯著性檢驗,從而接受原假設,不存在異方差性。
4.4.4 殘差正態性檢驗
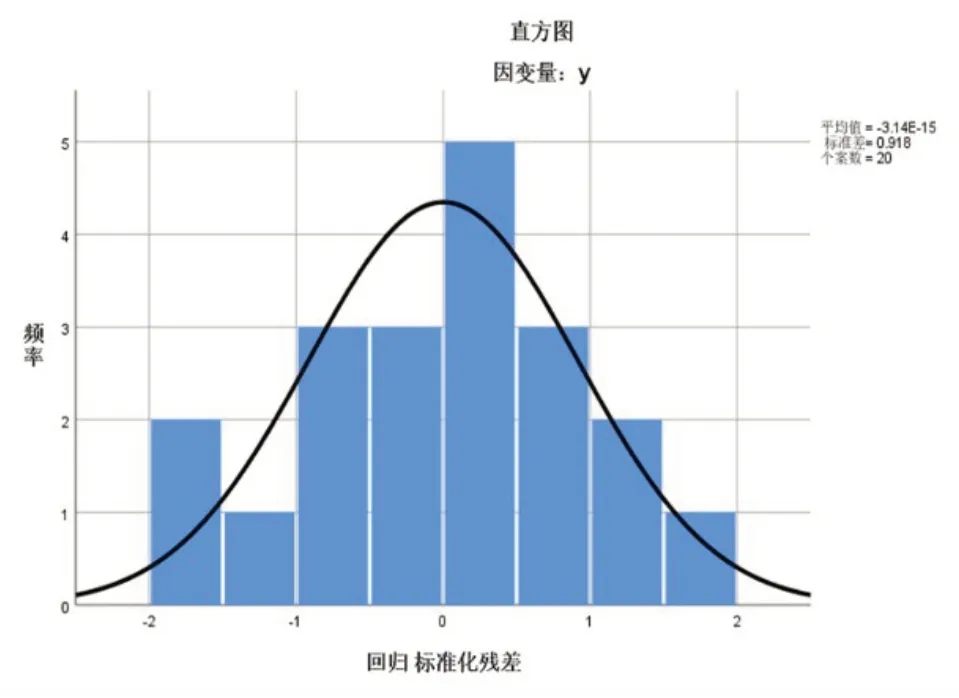
圖1 標準化殘差直方圖
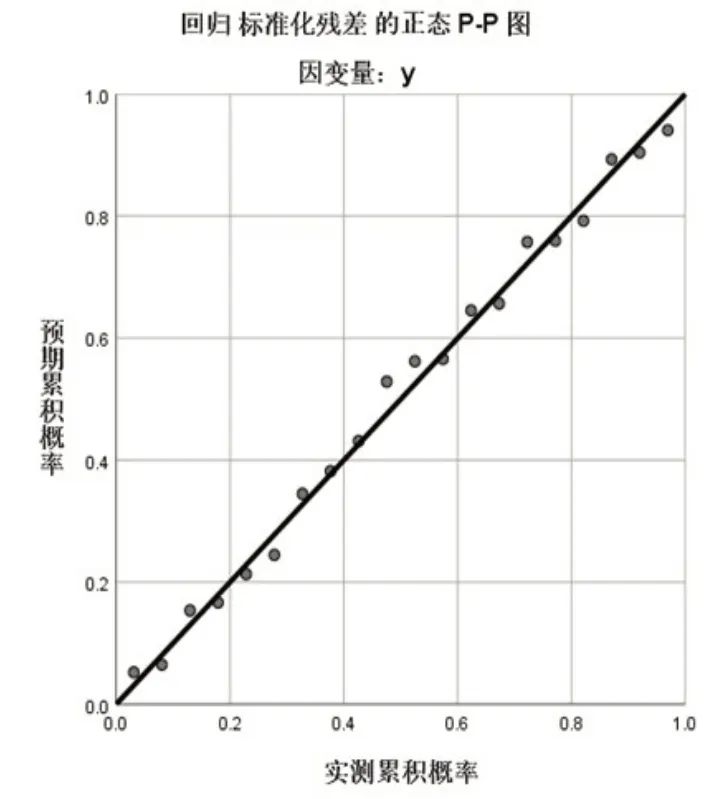
圖2 正態概率圖
從標準化殘差的直方圖(如圖1所示)可以看出,標準化殘差服從N(0,1)的正態分布;而且在正態概率圖(如圖2所示)中,散點大都圍繞在對角線上分布,故判斷殘差滿足正態性檢驗。
4.5 預測結果分析
運用建立的模型對一個實例進行預測,結果見表7與圖3。
從表7和圖3可以看出,最小誤差率為0.57%,最大誤差率為14.57%,平均誤差率為7.18%<10%。綜上所述可知該模型精確性較好,可以用來預測煙臺市的物流需求。

表7 預測結果分析

圖3 真實值與預測值擬合程度圖
5 建立煙臺市物流需求預測的GM(1,1)模型
5.1 GM(1,1)模型
對數列X(1)建立微分方程:

其中-a為發展系數,b為灰色作用量。記為有待估計確定的向量,則:

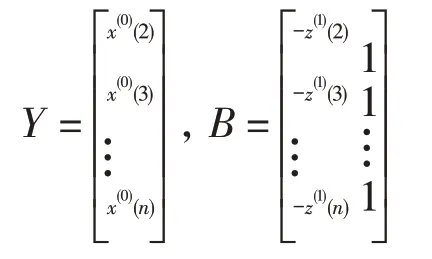
將式(2)求得的a帶入式(1)求解微分方程GM(1,1)模型:
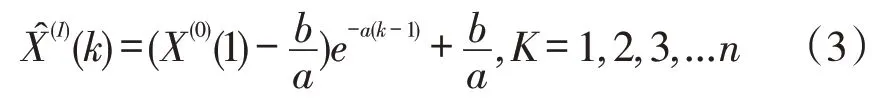
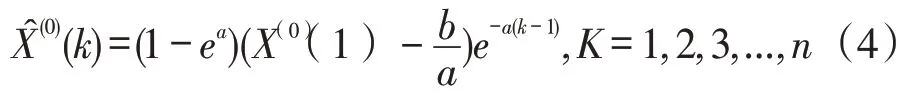
5.2 GM(1,1)回歸模型預測精度驗證
通過多元線性回歸可知,貨運量y與第一產業產值x1、第二產業產值x2、外貿進出口總額x6有較強的關聯性,所以可對這三個變量進行灰色GM(1,1)預測。建立GM(1,1)模型至少要有四個數據,本文以2013年-2016年X1,X2,X6數據來預測2017年的X1,X2,X6。將預測后的值代入線性回歸方程Y=13 687.670-105.356X1+20.426X2-28.167X6,驗證2017年貨運量擬合程度,并與2013-2016年貨運量y通過GM(1.1)模型直接預測2017年貨運量擬合程度做對比,分析結果如下:
(1)第一產業產值x1、第二產業產值x2、外貿進出口總額x6的數據分別為:

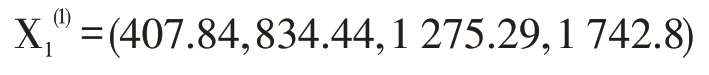



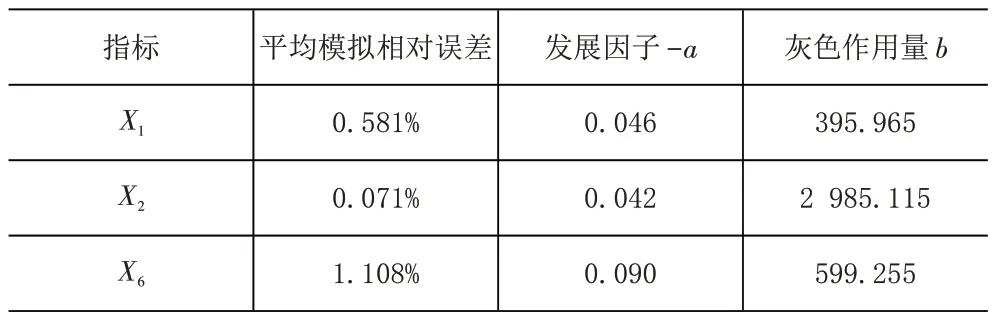
表8 2013-2016年灰色GM(1,1)作用量
由表8可知,-a<0.3 且平均相對誤差較小,可以用來預測2017 年 X1,X2,X6值,并將預測值帶入方程y=13 687.670-105.356X1+20.426X2-28.167X6,求得2017貨運量,所得結果見表9。

表9 GM(1,1)與多元線性回歸方程結合預測2017年貨運量
同理,根據煙臺市2013-2016年貨運量可得到原始數列X(0)=(20 121.90,19 771.70,19 930.28,22 360.90),對其作1-AGO 累加,生成新數列X(1)=(20 121.90,39 893.6,59 823.88,82 184.78) ,計算級比數列和光滑比數列分別為δ(t)=(1.983,1.500,1.374) ,p(t)=(0.983,0.500,0.374),當t>2 時,δ(t)∈[1,1.5)滿足灰指數律,此時,p(t)<0.55 符合準光滑條件,所以可以對X(1)建立GM(1,1)模型。
設X(1)的緊鄰均值生成序列為 Z(1),,其中K=1,2,3,...n,經計算得Z(1)=(30 007.750 0,49 858.750 0,71 004.350 0)),運用最小二乘法求得發展系數-a=0.064,b=17 483.198,-a<0.3 且平均相對誤差為2.396%,適合中長期預測,最終可得2017年貨運量預測值為23 457.633,見表10。

表10 GM(1,1)模型預測2017年貨運量
由表8和表9可知,GM(1,1)預測模型與多元線性回歸方程的有機結合,一方面保留了多元線性回歸中變量的相關關系,另一方面又充分利用了灰色GM(1,1)模型少數據建模及適用于中長期預測的優勢,使預測結果更加準確。
5.3 基于GM(1,1)回歸模型的預測分析
本文以2013-2017 年 5 年間的 X1,X2,X6數據預測2018-2022 年的 X1,X2,X6,計算過程不再贅述,平均模擬誤差率較小且-a <0.3,所以該模型適合中長期預測具體見表11-表13。將灰色GM(1,1)模型的輸出結果作為多元線性回歸預測方程的輸入,從而在比較全面考慮各影響因素的基礎上,實現GM(1,1)預測模型與多元線性回歸方程的優化結合,最終取得較高精度的預測結果。

表11 2013-2017年灰色GM(1,1)作用量
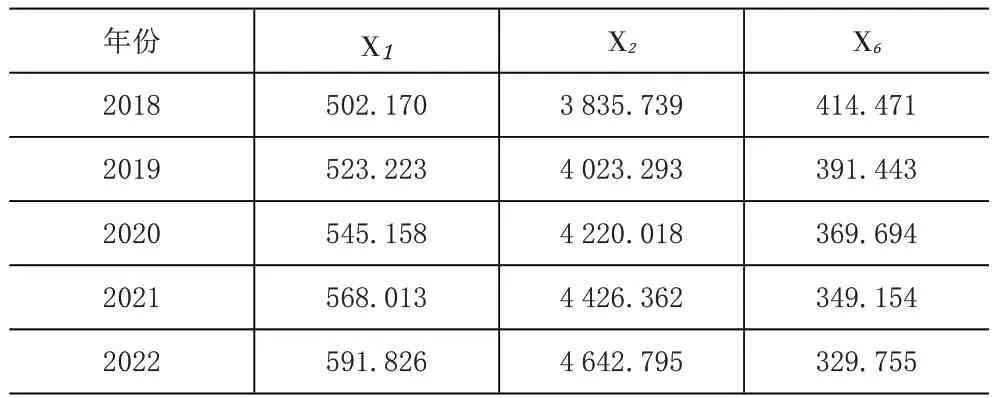
表12 2018-2022年主要需求指標預測結果
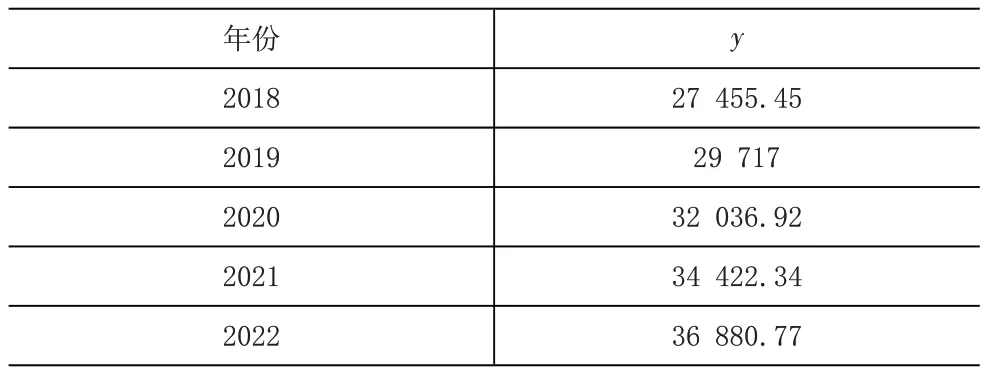
表13 2018-2022年貨運量預測
6 基本結論與對策建議
通過多元線性回歸分析,求得回歸方程y=13 687.670-105.356X1+20.426X2-28.167X6,可得出以下結論:在引入的8個變量中,第一產業產值X1、第二產業產值X2、外貿進出口總額X6對貨運量有顯著的影響。第一產業產值對物流需求表現為負影響,第二產業產值對物流需求表現為正影響,表明煙臺市已經脫離以第一產業拉動為主的物流發展階段,主要依靠第二產業;目前煙臺市正處于新舊動能轉換關鍵時期,這對傳統的物流提出了新的挑戰,要求物流在產業結構與功能上進行相應的調整,煙臺市想要擴大物流需求,有必要降低第一產業比例、提高第二產業的比例,加強產業結構調整優化。外貿進出口總額對物流需求表現為負影響,進出口業務對物流相關服務水平要求較高,煙臺市相應的物流基礎設施服務不是很完善,對物流需求的影響還沒有起到理想化的正向作用,需要進一步提高,尤其是要提高物流的信息化水平,加快改革創新,促進智慧型港口建設。
建立基于GM(1,1)回歸的煙臺市物流預測模型,將預測值與實際值進行比較,結果顯示誤差在可接受的范圍內,說明采用該模型對物流需求預測是可行的。從未來5年的預測數據可以看出,煙臺市的物流需求將會持續增長,不僅給煙臺物流的發展提供了重大的機遇,同時也對煙臺物流服務水平提出了更高的挑戰。我們要集合人力、物力、財力共同努力,推動煙臺市物流的快速發展,力爭在“十三五”期間把煙臺市打造成東北亞物流交通樞紐。

