單生產商-多客戶兩級供應鏈缺貨庫存行為分析
李群霞
(北京科技大學 東凌經濟管理學院,北京 100083)
1 引言
在傳統庫存管理環節下,供應鏈中的每個成員都有自己的庫存管理策略。由于各自的庫存管理策略相互封閉,因此不可避免地造成客戶的需求與生產商的生產不匹配、不協調現象。供應鏈庫存管理可以打破原有各自為政的庫存管理模式,體現了供應鏈的集成化管理模式,適應市場變化的要求。
Liao、Tsai 和Su[1]在批量訂貨庫存管理模型中允許延遲付款。Aggarwal 和Jaggi[2]假設產品存在變質現象,變質率服從指數分布。Goyal[3]是第一個在批量訂貨庫存管理模型中引入商業信用機制的人。Huang和Hsu[4]在供應鏈庫存管理模型中采用兩層商業信用機制,除生產商提供給零售商商業信用外,零售商也可以提供部分商業信用給客戶。Rau、Wu 和Wee[5]假設不存在缺貨,只研究缺陷品對供應鏈庫存的影響。Viswanathan和Piplani[6]研究共同補貨機制,供應商提供一個共同補貨的時間,要求所有客戶只能在這段時間內補貨。為了讓客戶更容易接受,供應商在這段時間內提供了價格折扣機制。Sucky[7]為了引起客戶的積極性,實現庫存聯合決策協調,提供給客戶多種議價機制。Sana[8]在三級供應鏈庫存管理模型中考慮了缺陷品對上級供應商和中級生產商的影響。Wu 和Ho[9]允許存在缺貨,將訂貨點作為決策變量,同時優化訂貨量、訂貨點、提前期和訂貨次數。李群霞[10]研究缺貨和缺陷品對庫存成本的影響,并采用模糊優化方法進行優化求解。Zhou和Wang[11]分析了缺貨和缺陷品對庫存成本的影響。李群霞等[12]假設供應鏈含有一個生產商和多個客戶,建立了供應鏈聯合庫存優化決策模型。
本文在文獻[12]基礎上對其作進一步研究,假設供應鏈中的多個客戶都存在缺貨情況,根據生產商的生產庫存水平變化特點和所有客戶的訂貨庫存水平變化特點,分別建立了生產庫存模型和缺貨訂貨庫存模型,由此確定了供應鏈缺貨庫存模型,在此基礎上,研究聯合優化決策方法以及在聯合優化決策下的客戶缺貨行為對供應鏈中各個成員的庫存成本和庫存決策參數的影響。
2 供應鏈庫存描述
文中所涉及的變量及含義見表1,變量中下標“m”表示生產商,下標“b”表示客戶,下標“bi”表示第i個客戶。

表1 變量及其含義
圖1只給出了三個客戶和一個生產商的兩級供應鏈庫存系統的例子。客戶1、客戶2 和客戶3 的起始庫存水平分別是Qb1-Sb1、Qb2-Sb2和Qb3-Sb3,他們的產品需求率分別為db1、db2和db3,當庫存消耗完,所有客戶開始缺貨,在各自的訂貨周期末達到最大缺貨量,分別為Sb1、Sb2和Sb3。假設每個客戶都能夠瞬時補貨,則庫存在訂貨周期結束或者在訂貨周期起始得到及時補充。對于生產商,以生產率Pm進行生產產品,因此庫存水平在不斷地變化中,通過客戶的訂貨及時地削減庫存水平。當時間到達Tm2時,生產商已生產能滿足所有客戶在Tm1周期內所需的產品,因此停止生產產品。當時間到達Tm1時,生產商的庫存水平正好降為0。
這里存在如下假設:
(1)每個客戶的庫存在每個訂貨周期結束或每個訂貨周期起始能夠瞬時補貨,補貨量或訂貨量Qbi >Sbi;
(2)每個客戶都存在缺貨現象;
(3)每個客戶的產品需求率是線性的;
(4)每個客戶的單位缺貨成本要大于單位持有成本;
(5)生產商不存在缺貨現象;
(6)生產商的產品生產率大于所有客戶的總需求率,因此生產商的產品生產時間Tm2小于生產時間間隔Tm1;
(7)生產商的生產量正好滿足所有客戶的訂貨量,這說明生產商需要生產等同數量的產品。
(8)生產商一次生產正好滿足所有客戶訂貨量的產品,生產完后停止生產。

圖1 供應鏈中各個成員的庫存水平變化情況
3 供應鏈缺貨庫存模型
3.1 缺貨訂貨庫存模型
客戶的平均庫存成本包括客戶的平均訂貨成本、平均持有成本和平均缺貨成本。
(1)平均訂貨成本:客戶的每次訂貨費用為Abi,每次訂貨可滿足客戶Tbi時間內的需求,因此平均訂貨成本,則平均訂貨成本可改為
(2)平均持有成本:客戶需求率dbi為常數,平均持有庫存水平,則持有成本=,平均持有成本=
(3)平均缺貨成本:客戶需求率dbi為常數,平均缺貨庫存水平則缺貨成本平均缺貨成本
綜上所述,客戶的平均庫存成本為:
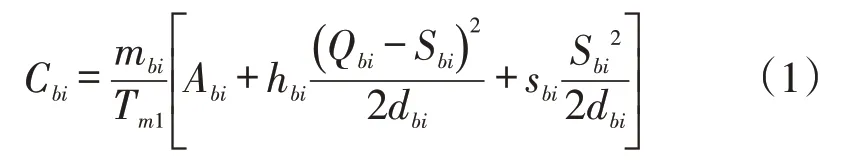
3.2 生產庫存模型
生產商的平均庫存成本包括平均生產準備成本和平均庫存持有成本。
(1)平均生產準備成本:生產商每次生產準備成本為Am,生產時間間隔為Tm1,因此平均生產準備成本
(2)平均庫存持有成本:如圖1所示,Tm1時間內,所有客戶的總需求率為,另外需求是線性的,因此總需求量為了滿足所有客戶的產品需求,生產商需要生產個產品。因為生產商的生產率要大于總需求率,即Pm>Db>0,因此生產商在Tm2<Tm1時間內就完成生產指標。因此生產商的平均庫存持有成本為:
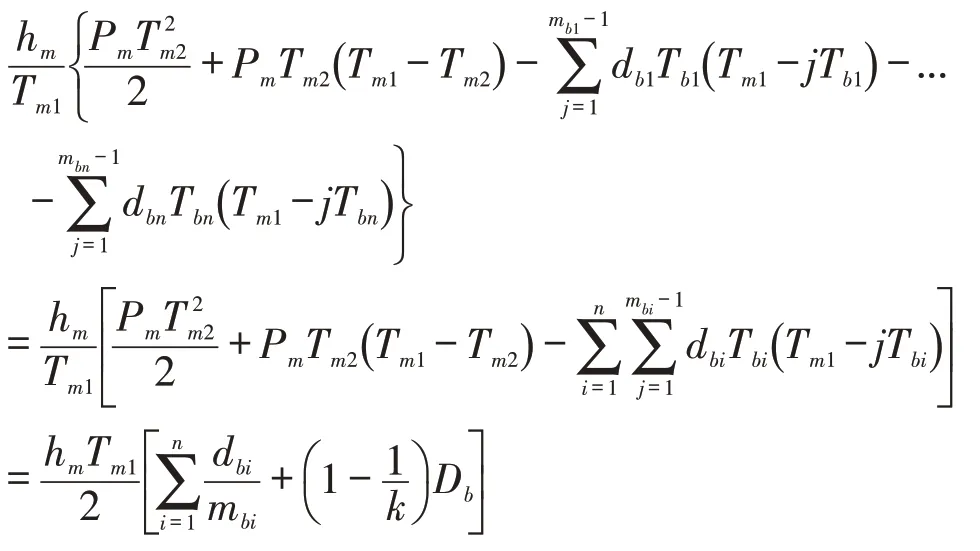
綜上所述,供應商的總平均庫存成本為
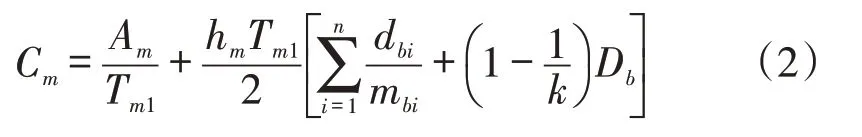
3.3 供應鏈缺貨庫存模型
結合式(1)的客戶缺貨訂貨成本模型和式(2)的生產商生產成本模型,供應鏈環境下的庫存模型,即供應鏈的總庫存成本為:
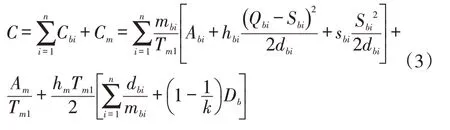
對上式中Sbi分別求一階導和二階導,有:
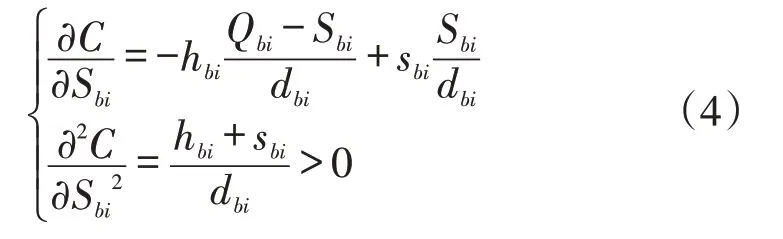
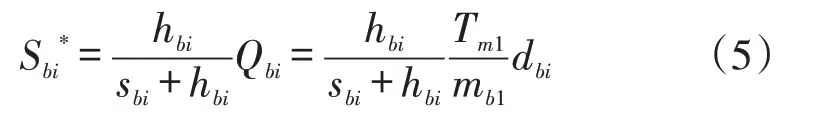
將其代入式(3),可得C:
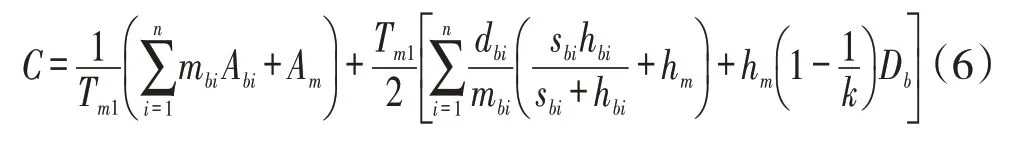
對上式中Tm1分別求一階導和二階導,有:
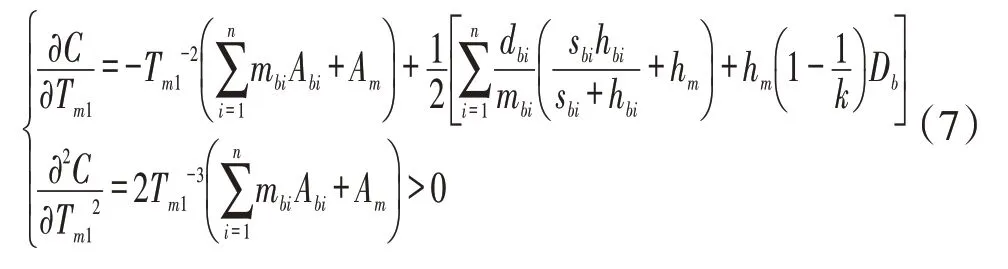
由式(7)的二階導大于0可知,式(6)存在最優生產時間間隔,保證式(6)存在最小的庫存成本值。令式(7)的一階導等于0,可得最優生產時間間隔
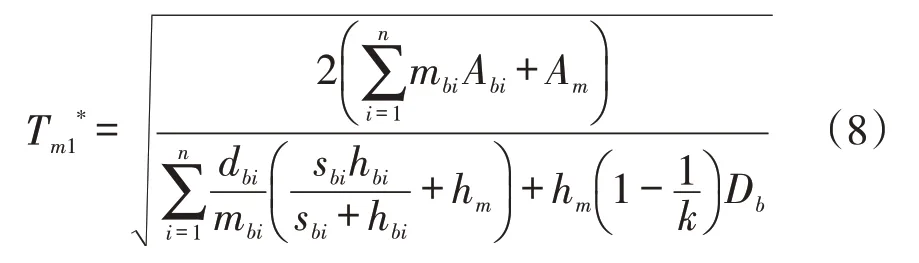
將其代入式(6),可得C:
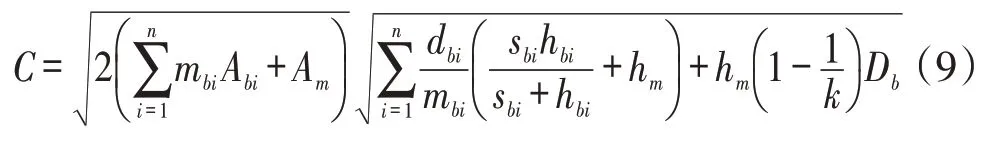
繼續對式(9)中訂貨次數mbi求一階導,并令其為0,即:

整理后可得:
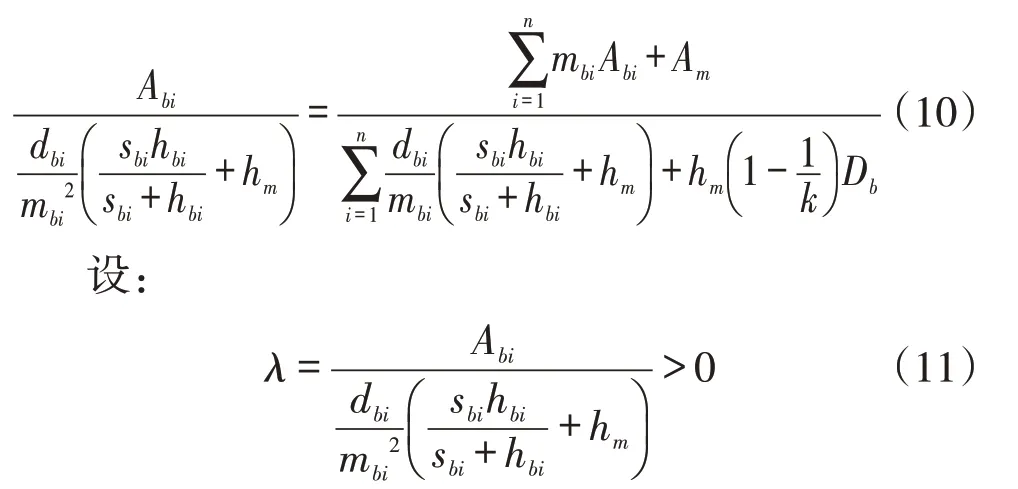
將式(11)代入式(10),并整理可得:
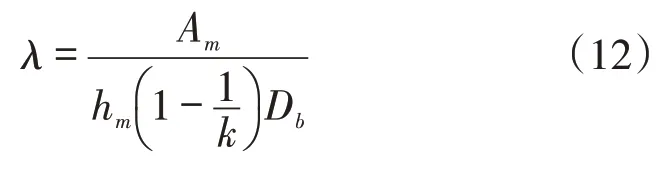
因k>1,則,因此λ>0假設成立。從式(12)可知,λ其實與mbi是無關的。對式(9)中訂貨次數mbi求二階導:

結合一階導推導出的式(11)和式(12),可獲得最優訂貨次數
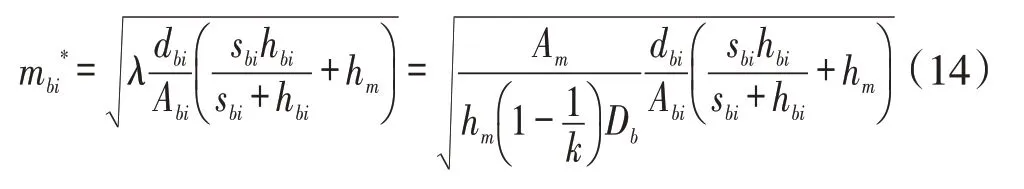
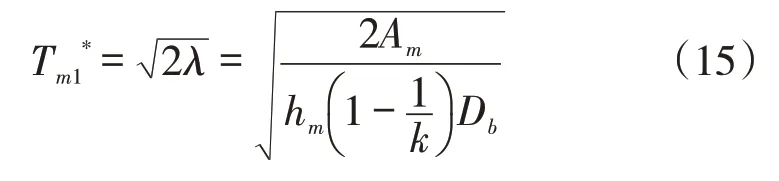
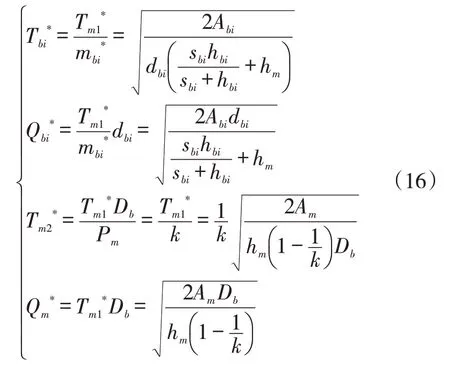
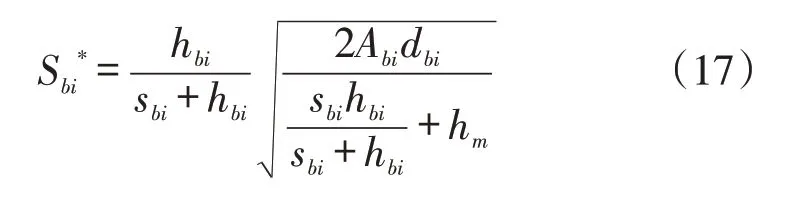
將式(14)-式(17)代入式(1)-式(3)可得客戶的最小庫存成本、生產商的最小庫存成本和供應鏈的最小庫存成本分別為:
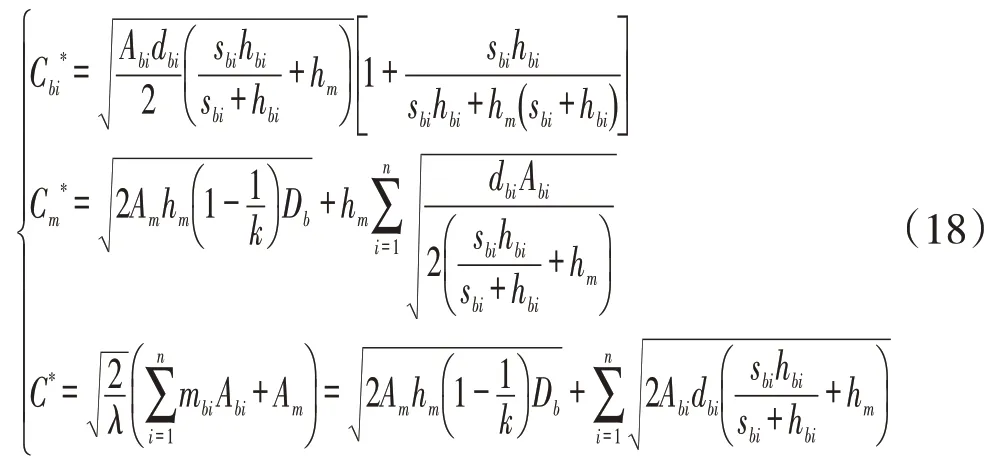
4 算例分析
假設供應鏈由一個供應商和三個客戶組成,其參數如下:
(1)客戶(一次訂貨):Ab1=150 元/次,Ab2=200元/次,Ab3=180元/次;db1=15 000 件/年,db2=10 000件/年,db3=8 000 件/年;hb1=15 元/件/年,hb2=20 元/件/年,hb3=25 元/件/年;sb1=30 元/件/年,sb2=25 元/件/年,sb3=35 元/件/年。
(2)生產商(一次生產):Am=30 000 元/次;Pm=60 000件/年;hm=8元/件/年。
將這些參數代入式(14)-式(18),可得供應鏈環境下各個成員的最優庫存參數和最小庫存成本。
(1)客戶1的最優訂貨次數、最優訂貨時間、最優訂貨量、最優缺貨量和最小庫存成本為:
(2)客戶2的最優訂貨次數、最優訂貨時間、最優訂貨量、最優缺貨量和最小庫存成本為:
(3)客戶3的最優訂貨次數、最優訂貨時間、最優訂貨量、最優缺貨量和最小庫存成本為:
(4)生產商的最優生產時間間隔、最優生產時間、最優生產量和最小庫存成本為:
(5)供應鏈的最小庫存成本為:C*=1.278 6e+06。
5 敏感性分析
5.1 缺貨量Sbi*對訂貨量Qbi*的影響
缺貨量Sbi*對訂貨量Qbi*的影響如圖2所示,對所有客戶的曲線變化趨勢都是一樣的,Sbi*與Qbi*成反比關系。缺貨量對客戶3的訂貨量影響更加明顯,因為隨著缺貨量增大,訂貨量下降得非常明顯。
5.2 缺貨量Sbi*對生產時間間隔Tm1*的影響

圖2 缺貨量Sbi*對訂貨量Qbi*的影響
缺貨量Sbi*對生產時間間隔Tm1*的影響如圖3所示,對所有客戶的影響都一樣,Sbi*與Tm1*沒有直接的聯系,這個也可以從式(15)得出,Tm1*只與生產商的準備成本Am、生產商的單位持有成本hm、生產商的生產率Pm和客戶的總需求率Db有關,與客戶的單位持有成本和單位缺貨成本無關,因此對于所有客戶,趨勢都是一樣的,都為水平直線的關系。
5.3 缺貨量Sbi*對訂貨次數mbi*的影響
缺貨量Sbi*對訂貨次數mbi*的影響如圖4所示,對所有客戶,Sbi*與mbi*成正比關系。根據曲線的斜率信息,可以確定缺貨量對客戶3的訂貨次數影響更大,對客戶2的訂貨次數影響最小。
5.4 缺貨量Sbi*對客戶庫存成本Cbi*的影響
缺貨量Sbi*對客戶庫存成本Cbi*的影響如圖5所示,Sbi*與Cbi*成正比關系。由曲線的斜率信息可知,對客戶3的影響最大,對客戶2的影響最小。
5.5 缺貨量Sbi*對生產商庫存成本Cm*的影響
缺貨量Sbi*對生產商庫存成本Cm*的影響如圖6所示,Sbi*與Cm*成反比關系。Sbi*對客戶3的庫存成本造成的影響最大,對客戶1 的影響次之,對客戶2的影響最小。
5.6 缺貨量Sbi*對供應鏈的總庫存成本C*的影響
缺貨量Sbi*對供應鏈的總庫存成本C*的影響如圖7所示,Sbi*與C*還是呈反比關系。缺貨量對客戶3的影響最大,對客戶1的影響次之,對客戶2的影響最小。供應鏈庫存成本包括客戶的庫存成本和生產商庫存成本,盡管缺貨量與客戶庫存成本的變化關系成正比關系,但是由于生產商的庫存成本遠遠大于客戶的庫存成本,因此生產商的庫存成本決定了缺貨量與供應鏈庫存成本之間的關系。由圖6可知,缺貨量與生產商的庫存成本成反比關系,因此缺貨量與供應鏈庫存成本的變化也成反比關系。
6 結語
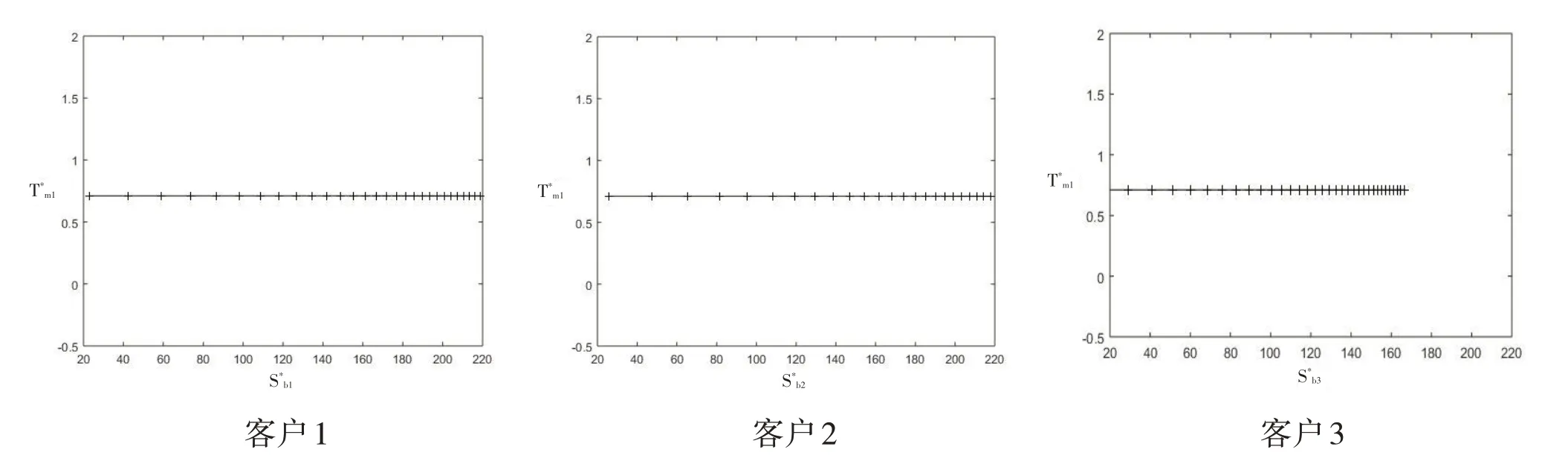
圖3 缺貨量Sbi*對生產時間間隔Tm1*的影響
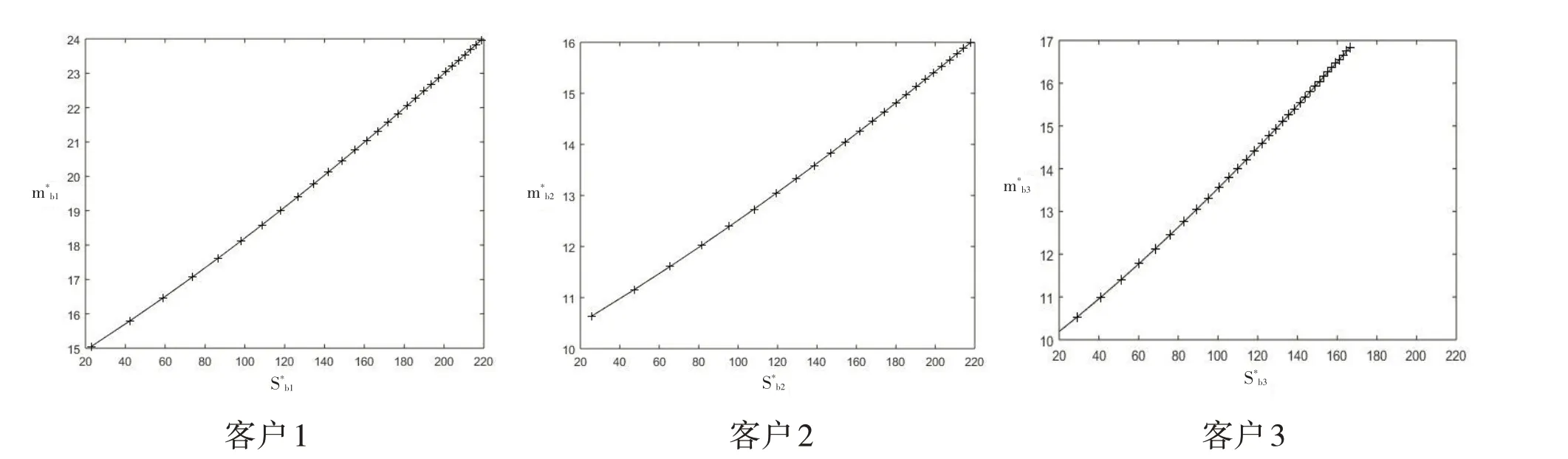
圖4 缺貨量Sbi*對訂貨次數mbi*的影響
本文對一個生產商和多個客戶構成的兩級供應鏈庫存系統進行了研究,假設所有客戶都存在缺貨現象,構建了以缺貨量、訂貨次數和生產時間間隔為自變量、以平均庫存成本為目標函數的供應鏈缺貨庫存管理模型。聯合優化決策方法,在保證獲得最小供應鏈庫存成本基礎上,可得到最優缺貨量、最優訂貨次數和最優生產時間間隔。敏感性分析表明缺貨量對訂貨次數和客戶庫存成本成正比關系,但是因為對生產商的庫存成本成反比的關系,導致整體上對供應鏈的庫存成本也成反比關系。
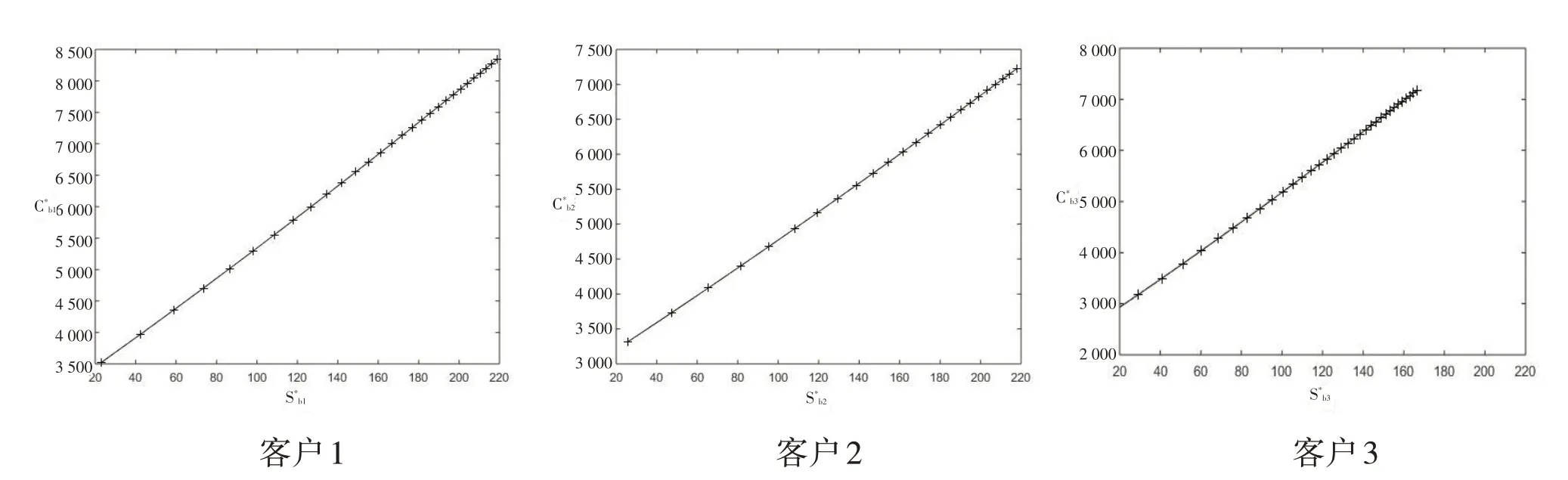
圖5 缺貨量Sbi*對客戶庫存成本Cbi*的影響
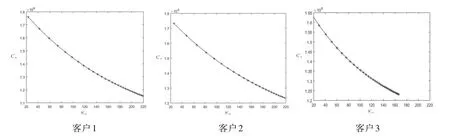
圖6 缺貨量Sbi*對生產商庫存成本Cm*的影響

圖7 缺貨量Sbi*對供應鏈庫存成本C*的影響

