統計與概率擴大“朋友圈”

■廣西來賓高級中學 覃尚猷 楊 佶 胡利潔

在大數據時代，科學技術飛速發展，隨著高中數學課程不斷改革，“統計與概率”既是高中階段數學課程的主線，又是大學數學教育的基礎課程，成了高考出題的新亮點，特別是2019年全國Ⅰ卷將“統計與概率”題放在第21題，讓人刮目相看。近年來，有不少的統計與概率題注重情境生活化、素材新穎化、問題實用化，同學們分析問題與解決問題的能力不斷提升才能解決“朋友圈”不斷擴大的統計與概率問題，下面選取幾道題與大家共同賞析。

一、概率與數列交匯

例1為了治療某種疾病，研制了甲、乙兩種新藥，希望知道哪種新藥更有效，為此進行動物試驗。試驗方案如下：每一輪選取兩只白鼠對藥效進行對比試驗。對于兩只白鼠，隨機選一只施以甲藥，另一只施以乙藥。一輪的治療結果得出后，再安排下一輪試驗。當其中一種藥治愈的白鼠比另一種藥治愈的白鼠多4只時，就停止試驗，并認為治愈只數多的藥更有效。為了方便描述問題，約定：對于每輪試驗，若施以甲藥的白鼠治愈且施以乙藥的白鼠未治愈則甲藥得1分，乙藥得-1分；若施以乙藥的白鼠治愈且施以甲藥的白鼠未治愈則乙藥得1分，甲藥得-1分；若都治愈或都未治愈則兩種藥均得0 分。甲、乙兩種藥的治愈率分別記為α 和β，一輪試驗中甲藥的得分記為X。

(1)求X 的分布列；

(2)若甲藥、乙藥在試驗開始時都賦予4分，pi(i=0，1，…，8)表示“甲藥的累計得分為i時，最終認為甲藥比乙藥更有效”的概率，則p0=0，p8=1，pi=api-1+bpi+cpi+1(i=1，2，…，7)，其中a=P(X=-1)，b=P(X=0)，c=P(X=1)。假設α=0.5，β=0.8。

①證明：{pi+1-pi}(i=0，1，2，…，7)為等比數列；

②求p4，并根據p4的值解釋這種試驗方案的合理。

解析：(1)由題意可知X 的所有可能取值為-1，0，1，所以P(X=-1)=(1-α)β，P(X=0)=αβ+(1-α)(1-β)，P(X=1)=α(1-β)。

所以X 的分布列為表1：

(2)因為α=0.5，β=0.8，所以a=0.5×0.8=0.4，b=0.5×0.8+0.5×0.2=0.5，c=0.5×0.2=0.1。

①因為pi=api-1+bpi+cpi+1(i=1，2，…，7)，即pi=0.4pi-1+0.5pi+0.1pi+1(i=1，2，…，7)，整理可得5pi=4pi-1+pi+1(i=1，2，…，7)，所以pi+1-pi=4(pi-pi-1)(i=1，2，…，7)。

所以{pi+1-pi}(i=0，1，2，…，7)是以p1-p0為首項，4為公比的等比數列。

②由①知pi+1-pi=(p1-p0)·4i=p1·4i，所以p8-p7=p1·47，p7-p6=p1·46，…，p1-p0=p1·40。

以上各式相加可得p8-p0=p1·(40+41+…+47)

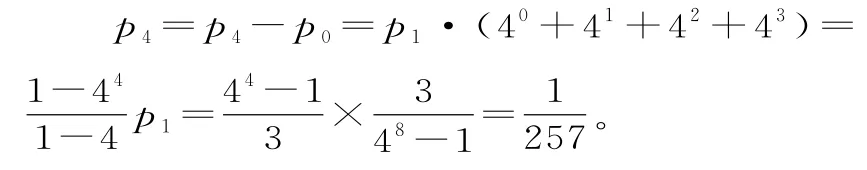
p4表示最終認為甲藥是更有效的。由計算結果可以看出，在甲藥治愈率為0.5，乙藥治愈率為0.8時，認為甲藥更有效的概率為≈0.003 9，此時得出錯誤結論的概率非常小，說明這種實驗方案合理。

點評：本題考查離散型隨機變量分布列的求解、等比數列的證明、求數列通項公式和數列中的項的問題。本題是在概率與數列知識交匯處出題，具有較強的綜合性，對同學們分析和解決問題的能力有較高要求。要過三關：(1)閱讀關；(2)數列關；(3)概率運算關。

二、概率與立體幾何交叉

例2設ξ 為隨機變量。從棱長為1的正方體的12條棱中任取兩條，當兩條棱相交時，ξ=0；當兩條棱平行時，ξ 的值為兩條棱之間的距離；當兩條棱異面時，ξ=1。

(1)求概率P(ξ=0)；

(2)求ξ 的分布列，并求其數學期望E(ξ)。

解析：(1)若兩條棱相交，則交點必為正方體8個頂點中的1個，過任意1個頂點恰有3 條棱，所以共有對相交棱，因此

所以隨機變量ξ 的分布列為表2：

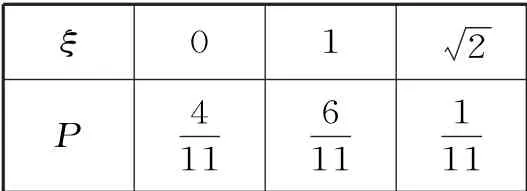
表2

點評：本題在立體幾何知識的環境下考查概率、分布列、數學期望，是概率、立體幾何、組合等知識的綜合，能否“翻譯”成概率知識成為關鍵。要過三關：(1)立體幾何關；(2)概率關；(3)排列組合運算關。

三、概率與面積相伴

例3設A，B，C，D，E，F為單位圓上的六等分點。現任選其中三個不同點構成一個三角形，記該三角形的面積為隨機變量S。

(2)求S 的分布列及數學期望E(S)。

解析：(1)從六個點中任選三個不同點構成一個三角形共有種不同選法，其中S=的是有一個角為30°的直角三角形，共6×2=12(種)，所以

(2)S 的所有可能取值

結合(1)知S 的分布列為表3：

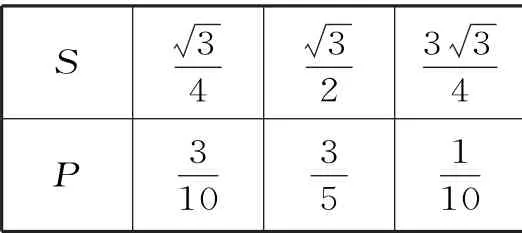
表3

點評：本題考查概率、離散型隨機變量的分布列及數學期望的求法，是概率與面積、組合等相關知識的綜合題，難度不是很大，解題時要認真審題，其中“翻譯成“有一個角是30°的直角三角形”是解題的關鍵，畫出圖形有助于問題的解決，注意排列組合知識的運用。要過三關：(1)理解“翻譯”關；(2)平面幾何關；(3)概率、排列組合運算關。

觀察近幾年高考題中的統計概率題，具有情境新、素材新、題型新等特點，與數列交匯，同立體幾何交叉，與面積相伴，“朋友圈”不斷擴大，在統計概率不斷招兵買馬擴大隊伍的同時，對同學們綜合解題能力的要求不斷提升，需要在題目特定的情境下冷靜分析題目，學會將復雜的題意簡單地“翻譯”出來，再用概率的知識解決。