碳交易政策與碳排放

李艷芹 李宗堯 張騫

摘要：以科斯產權定理為理論基礎，建立了關于碳排放量和碳排放強度的多時點雙重差分模型，對2007—2017年我國30個省級行政區（不含港澳臺和西藏自治區）的相關面板數據進行實證檢驗，以考察碳交易政策對碳排放的影響。多時點雙重差分結果顯示：碳交易政策對減少碳排放量具有顯著促進作用，隨著實行時間的推移，該政策的減排效果逐漸增大；碳交易政策的實施有利于降低碳排放強度，且政策影響同樣逐年增大，與該政策對碳排放量的影響相比，相關系數明顯更大；在對碳排放量和碳排放強度的影響過程中，經濟水平和技術水平等因素的影響效果比較顯著，而產業結構和人口規模等變量到目前為止尚未表現出明顯影響；特別地，我國二氧化碳排放量與經濟發展水平之間滿足EKC假說，二者之間存在倒“U”形曲線關系。

關鍵詞：碳交易；碳排放量；碳排放強度；多時點雙重差分法

中圖分類號：F830.33文獻標識碼： ADOI：10.3969/j.issn.1003-8256.2020.06.010

開放科學（資源服務）標識碼（OSID）：

0引言

20世紀以來，隨著工業化、城市化的發展以及全球人口的迅速增長，全球變暖已成為當今人類無法回避的問題。全球變暖不僅會加劇冰川消融、引發一系列生態問題，還會對人類健康造成嚴重威脅，妥善處理經濟發展與環境保護之間的關系成為各國共同面臨的挑戰。在物理學中，二氧化碳、甲烷等溫室氣體在一定的物理條件下會產生溫室效應，從而導致全球變暖現象的出現，而在《聯合國氣候變化框架公約的京都議定書》中規定控制的六種溫室氣體中，二氧化碳對溫室效應的貢獻率近一半，成為造成溫室效應的最主要溫室氣體之一，因此，控制碳排放成為緩解全球變暖的重要途徑。根據世界銀行發布的全球碳排放相關數據顯示，2005年以來我國碳排放量直線上升，目前已成為世界第一大碳排放國，減排壓力巨大。此外，按照2014年中美兩國達成的溫室氣體減排協議，我國將力爭在2030年左右開始減少溫室氣體排放量，更為本就困難的減排任務增加了難度系數。因此，行之有效的碳減排工具對減排任務的完成十分重要。

碳交易，即二氧化碳排放權交易，最早是在1997年的《京都議定書》中提出，該協議將市場機制作為解決溫室效應的新途徑，使得二氧化碳排放量可以在碳交易市場進行買賣。國際上以歐盟的ETS、英國的ETG、美國的CCX和澳大利亞的NSW等四大碳交易所規模最大，我國也分別于2012、2013和2017年陸續在北京、上海、重慶、湖北、天津、深圳、廣東、福建等8省市開啟試點工作。自碳交易試點工作啟動以來，各試點省市的交易量逐年攀升，2019年底全國碳交易試點的碳交易總量突破9200萬噸，其中廣東省以4538萬噸的交易量占據第一。

理論上，碳交易依托科斯定理，將碳排放權視為一種產權，而產權明晰才能避免“公地的悲劇”，因此，碳交易政策理應可以在一定程度上有助于實現碳減排目標。雖然國內碳交易市場的啟動和國際碳交易市場存在一定時差，但是國內外關于碳交易政策效果的研究在很多層面趨同。在研究結果層面，國內外多數研究認為該政策對環境改善具有顯著的促進作用[1-5]，碳交易政策值得在全國范圍內推廣，也有些研究認為到目前為止，該政策對于降低碳排放強度并無顯著效果[6]，是否應該推廣仍然值得商榷。在研究方法層面，主要采用CGE模型研究碳交易及其影響[7-8]，也有通過碳交易機制仿真模型測算了該政策對經濟和環境的影響[9-10]；除情景模擬分析外，合成控制法和雙重差分法（DID）則是近幾年相關研究的重要方法，陳醒等[11]采用合成控制法分別分析了各碳交易試點的碳減排效果，范丹等[12]綜合運用了雙重差分模型和全局DEA框架檢驗碳排放權交易機制是否支持技術創新的“弱波特假說”，馬曉偉[13]、任亞運[5]以及路正南等[3]在分析碳交易政策的減排有效性時同樣采用了雙重差分法。綜合對比情景分析法和雙重差分法，由于前者受情景設定的影響較大，在分析碳交易政策的有效性方面，雙重差分法則能反映出相對真實的政策效果；同時，以上有關雙重差分法的研究中，雖然關于政策的起始時點稍有差別，但是都將各個試點的起始時間歸為同一年內，考慮到各試點省市的相關工作開始年份不同，本文擬在傳統雙重差分模型的基礎上區分不同的起始時間，采用多時點雙重差分模型分析我國碳交易政策對碳排放的影響。

1模型設計和數據說明

1.1模型設定

本文將我國在各試點省市實行的碳交易政策視為一次“準自然實驗”，以碳排放量和碳排放強度作為衡量碳排放水平的兩個替代指標，采用多時點雙重差分法實證分析該政策分別對于碳排放量和碳排放強度的影響。其中，福建省于2017年正式啟動碳交易，深圳市的多個指標均包含在廣東省，鑒于數據的完整性和可得性，本文將2012年的北京、上海、重慶以及2013年的湖北、天津、廣東等6個試點省級行政區作為處理組，其余24個非試點省級行政區作為控制組（鑒于數據可得性，不含港澳臺和西藏自治區）。為消除個體和時間差異，在多時點雙重差分模型中加入個體效應和時點效應，使之成為控制雙向固定效應的多時點雙重差分模型，設定關于碳排放量和碳排放強度的基礎模型如下：

其中，CO2表示二氧化碳排放量，WCO2表示二氧化碳排放強度，α0、β0均為常數項，Dit為政策虛擬變量，當且僅當i為北京、上海、重慶對應的編號且t為2012與i為湖北、天津、廣東對應的編號且t為2013時，Dit為1，其他均為0，Zit表示控制變量，μi和τt分別表示個體效應和時點效應，εit表示標準殘差項。

1.2數據來源與變量說明

本文選取2007—2017年我國30個省區（不含港澳臺和西藏自治區）的面板數據，所有原始數據來源于《中國統計年鑒》《中國能源統計年鑒》《中國環境統計年鑒》和《中國城市數據庫》，具體的指標選取和核算方法如下：

（1）碳排放量的核算。本文以IPCC準則為依據并且按照IPCC所給出的能源碳排放系數進行折算，得出各省二氧化碳排放量，測度公式為：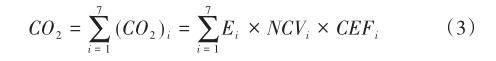

其中，i表示第i種能源，E表示能源消耗量，NCV表示該種能源的平均低位發熱量，單位為千焦/千克，CEF表示能源的二氧化碳排放系數，單位為千克/太焦。

（2）被解釋變量。各省級行政區的碳排放量即為按照式1所得數據，碳排放強度則為碳排放量與各省總產值之比，分別對二者取對數，用lnCO2和lnWCO2分別表征各省碳排放量和碳排放強度。

（3）控制變量。很多研究表明，碳排放的影響因素主要是通過結構效應、技術效應和規模效應來影響碳排放的[14—21]。結合IPAT模型和Kaya恒等式，同時參考Auff-hanner等和宋德勇等的方法，選擇產業結構、技術水平、人口規模和經濟水平作為控制變量。其中，產業結構（stru）用第二產業產值在總產值中所占比重來表示，技術水平（tech）用單位產值所需能源消耗量來表示，人口規模（popu）各省級行政區的人口密度表示，經濟水平（lngdp）則用各省對應各年的總產值的對數來表示。此外，由于碳排放量與經濟發展水平之間存在倒“U”形曲線關系[22—24]，因此在對碳排放量進行多時點雙重差分的過程中，要同時加入經濟水平的一次方項（lngdp）和二次方項（lngdp2），而碳排放強度相關模型中則只需加入經濟水平的一次方項（lngdp）。

2多時點雙重差分檢驗

2.1碳排放量的多時點雙重差分結果與分析

在針對碳排放量的實證檢驗過程中，以模型（1）作為基礎模型，不加入任何控制變量，在此基礎上分別加入經濟水平的一次方項與二次方項、產業結構、技術水平、人口規模等控制變量得到模型（4）到模型（7），采用多時點雙重差分法得到碳交易政策對碳排放量的影響結果如表1所示。

表1中，核心解釋變量Dit的系數符號與顯著性水平基本一致，控制變量經濟水平和技術水平均在1%水平上顯著，所有變量的系數符號均未發生變化，說明碳交易政策虛擬變量和經濟水平、技術水平等變量均通過了顯著性檢驗，且估計結果比較穩健。

觀察核心解釋變量Dit可知，該變量的回歸系數均為負，且在1%水平上顯著，說明碳交易政策對碳排放量具有明顯抑制作用，碳交易政策對于碳減排具有顯著促進作用。

控制變量中，lngdp在模型（4）到模型（7）中回歸系數顯著為正，lngdp2對應的回歸系數則均顯著為負，說明我國經濟發展水平與碳排放量之間存在倒“U”形曲線關系，證實了已有的相關研究結論[22-24]；tech的回歸系數在模型（6）和（7）中均在1%水平上顯著為負，說明技術水平的提高有助于推動碳減排的實現；stru和popu兩個控制變量均未通過顯著性檢驗，表明當前我國各省級行政區的碳排放量與人口規模和產業結構并無顯著相關關系。

2.2碳排放強度的多時點雙重差分結果與分析

在針對碳排放強度的實證檢驗過程中，以模型（2）作為基礎模型，不加入任何控制變量，在此基礎上分別加入經濟水平的一次方項、產業結構、技術水平、人口規模等控制變量得到模型（8）到模型（11），采用多時點雙重差分法得到碳交易政策對碳排放量的影響結果如表2所示。

表2中，核心解釋變量Dit在模型（2）和模型（8）到模型（11）中均通過了1%的顯著性檢驗，且對應的回歸系數符號一致，經濟水平、技術水平等控制變量和常數項也都在1%的水平下顯著，產業結構的回歸系數在10%水平下通過了顯著性檢驗，且以上所有控制變量回歸系數的符號在各模型下均一致，顯示該多時點雙重差分結果比較穩健，碳交易政策等變量對碳排放強度具有顯著影響。

在未加入任何控制變量之前，碳交易政策虛擬變量Dit的回歸系數為-0.1971，而在逐漸加入其他控制變量之后，尤其是在模型（11）中，Dit的回歸系數變為-0.1493，一方面表明了碳交易政策與碳排放強度顯著負相關，碳交易政策的實行有利于降低碳排放強度，另一方面說明，在加入經濟水平等多種控制變量以后，碳交易政策對降低碳排放強度的貢獻率下降；控制變量中，經濟水平、技術水平均與碳排放強度顯著負相關，表明了經濟水平的提高和技術水平的上升對碳排放強度的降低具有重要促進作用；popu未通過模型（11）的顯著性檢驗，表明目前我國人口規模對碳排放強度的解釋力相對較弱，人口密度的大小尚未對碳排放強度造成顯著影響。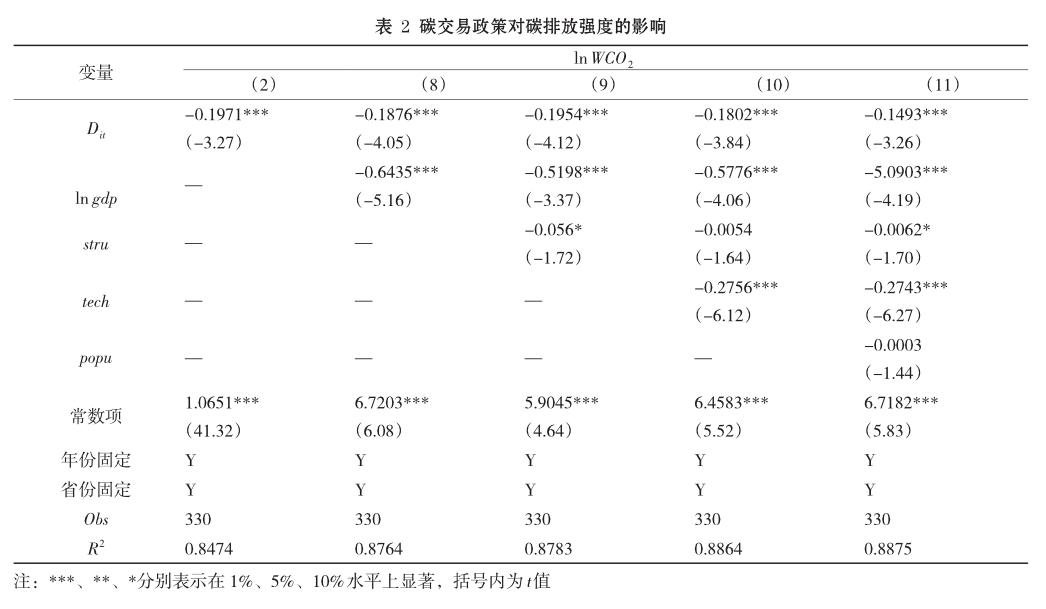

3穩健性和適用性檢驗

傳統的雙重差分法要求實驗或研究政策必須滿足隨機分組、處理變量與其他可能影響實驗結果的變量無關、處理組和控制組具有共同趨勢等前提條件，該要求也同樣適用于多時點雙重差分法。因此，為了檢驗碳交易政策是否滿足該要求，需要進行政策干預時間隨機性檢驗、分組隨機性檢驗、控制組不受試驗影響檢驗和共同趨勢檢驗。

3.1政策干預時間的隨機性檢驗

碳交易政策的發生時間必須是隨機選擇的，才能確保估計量的外生性[3]。根據陳林等[25]的改進建議，參照路正南等的相關研究，本文以2007—2017年間我國30個省級行政區的碳排放量和碳排放強度數據為基礎，對比分析二者的變化趨勢，觀察碳交易政策的發生時間是否滿足隨機性假設。期間我國各年碳排放量和碳排放強度趨勢圖如圖1所示：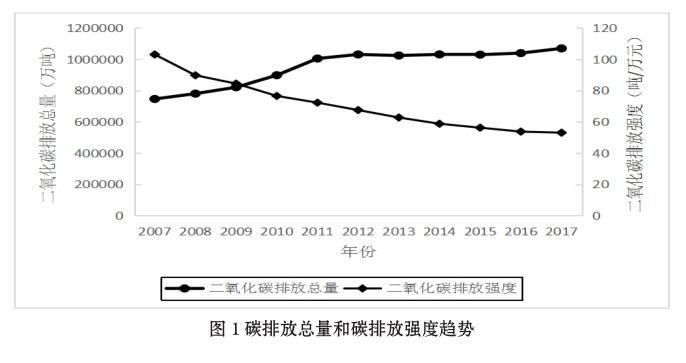

圖1中，2007—2017年間，碳排放總量呈逐年上升態勢，碳排放強度逐年下降的趨勢明顯，在2012年和2013年等碳交易政策集中發生年份，二者并無明顯異常波動，且在此之前的2007—2011年和之后的2014—2017年間，碳排放總量和碳排放強度走勢均較平穩，不存在異常值，表明碳交易政策發生時點的選擇與二者無關，該政策的干預時間滿足隨機性要求。

3.2分組的隨機性檢驗

為避免由樣本選擇帶來的回歸偏誤，處理組和控制組必須滿足隨機分組的要求，即控制組的選擇要具有隨機性。參照周晶等[26]的方法，本文以所有省區2013年前的碳排放量和碳排放強度數據為基礎，對各省對應的碳排放量和碳排放強度在全國范圍內進行排名，并篩選出2007—2012年北京等6個試點省級行政區的排名數據，制成表3。

如表3，在全國范圍內的二氧化碳排放量排名中，廣東和湖北基本處于前1/3位次水平，上海基本處于前2/3位次水平，重慶、北京和天津則處于后1/3位次水平，各試點省區的碳排放量全國排名所處區間較分散，未出現集中趨勢；在全國范圍內的二氧化碳排放強度排名中，重慶和湖北位于前2/3位次水平，北京、上海、天津和廣東等省區則位于后1/3位次水平，其中天津基本處于后1/3位次水平的前端，各試點省區的碳排放強度全國排名仍然未出現大面積集中趨勢。表明無論是在碳排放量層面還是碳排放強度層面，處理組和控制組的選取均滿足隨機性要求。

3.3控制組不受碳交易政策影響檢驗

如果除北京、廣東等試點省區外，其他非試點省區同樣受到碳排放政策影響的話，則無法使用多時點雙重差分法對模型進行回歸。因此，需要通過反事實檢驗來衡量非試點省區是否受碳交易政策的影響。在進行反事實檢驗過程中，首先剔除北京等試點省區，在剩下的24各省區中，依次不放回抽取6個省區編號，其中，前3個編號作為2012年實行碳交易政策省區，其余3個作為2013年實行碳交易政策省區，本文通過普通抓鬮法獲得反事實檢驗省區分別為：2012年的遼寧、新疆和浙江，2013年的山西、福建和安徽。假設該6省區為碳交易試點省區，以模型（1）和模型（2）為基礎，同樣采用多時點雙重差分法分別對碳排放量和碳排放強度進行回歸，回歸結果如表4所示，其中模型（11）和模型（13）為未加入任何控制變量的原始多時點雙重差分模型，模型（12）和模型（13）則為加入經濟水平、產業結構、技術水平和人口規模等控制變量的新模型。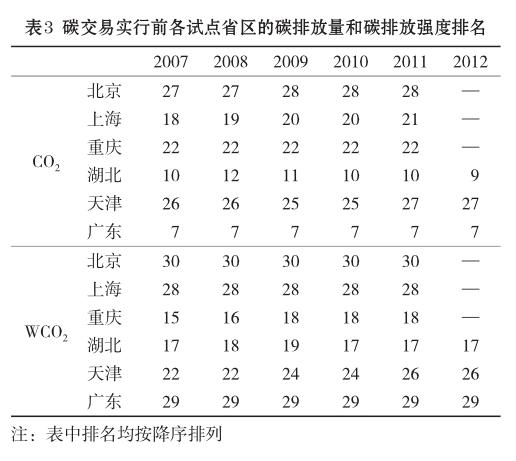

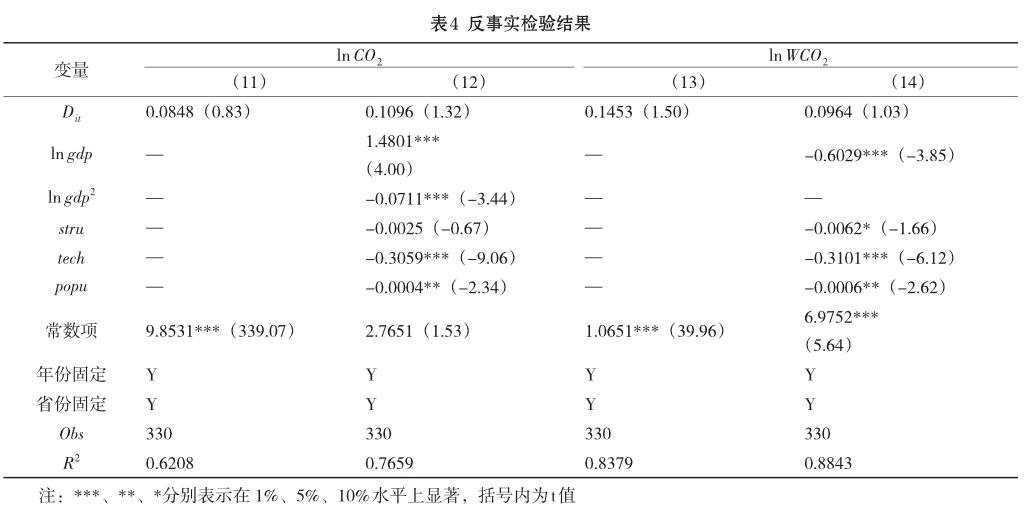
表4中，碳交易政策虛擬變量Dit在模型（11）到模型（14）中均不顯著，表明碳交易政策未對遼寧、山西等非碳交易試點地區的碳排放量和碳排放強度造成影響。同時，結果顯示經濟水平、技術水平和人口規模等控制變量對碳排放量和碳排放強度影響顯著，且碳排放量與經濟發展水平同樣滿足倒“U”形曲線關系，進一步證明了回歸結果的穩健性。

3.4共同趨勢檢驗和動態效應分析

在使用傳統的雙重差分法分析政策效果之前，處理組和控制組的被解釋變量具有共同趨勢是最重要的前提條件之一，否則，雙重差分結果沒有任何意義，該條件同樣適用于多時點雙重差分法。共同趨勢檢驗有多種方法，目前學界廣泛使用的事件研究法是其中之一。事件研究法即ESA方法，將其應用在多時點雙重差分法中，不僅可以檢驗被解釋變量的共同趨勢，還可以將政策效果在時間維度上清楚地展現出來，因此，將二者結合的方法又被稱為靈活的DID或者政策的動態效應。由于該方法優勢明顯，本文在進行共同趨勢檢驗時將ESA方法加入多時點雙重差分模型中，分析碳交易政策實行前各省區在碳排放量和碳排放強度方面是否具有共同趨勢，同時分析政策實行后的動態變化效果。

3.4.1碳排放量的共同趨勢與動態效應分析

圖2中，碳交易政策實行前3年的碳排放量與政策的相關系數接近于0，表明該政策實施前處理組和控制組的碳排放量具有共同趨勢；碳交易政策實施后的5年里，相關系數均為負值，且相關系數的絕對值隨時間的推移而增大，表明該政策的出現對減少碳排放量有明顯的促進作用，且時間越久，該政策的減排效果越大。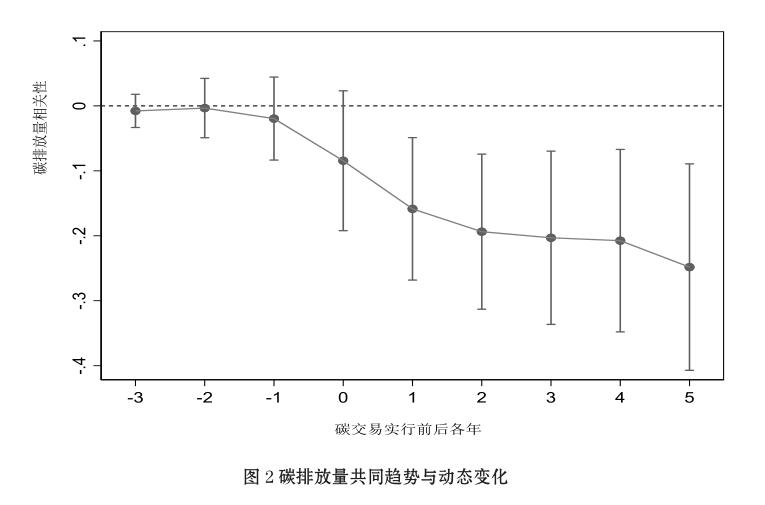

3.4.2碳排放強度的共同趨勢與動態效應分析

圖3中，碳交易政策實行之前的3年內，該政策對碳排放的影響系數幾乎為0，表明處理組和控制組的碳排放強度滿足共同趨勢假設；在該政策實施后的5年里，相關系數變化趨勢類似于碳排放量的相關系數變化，均為負值且絕對值逐年增大，與之不同的是，碳排放強度的相關性曲線下降趨勢比較平緩且絕對值整體偏大，表明碳交易政策不僅對碳排放強度具有持續增大的負效應，而且同該政策對碳排放量的影響相比，對碳排放強度的影響更平穩且效果更大。

4結論與建議

為了考察碳排放權交易政策對碳排放的影響，本文選取碳排放量和碳排放強度作為衡量碳排放的替代指標，構建了關于碳排放量和碳排放強度的多時點雙重差分模型，以北京、天津等6個碳交易試點省級行政區作為處理組，其他24個非試點省區作為對照組，對2007—2017年我國30個省級行政區（不含港澳臺和西藏自治區）的相關面板數據進行實證檢驗，結論如下：

（1）碳交易政策對減少碳排放量具有顯著促進作用，隨著實行時間的推移，該政策的減排效果逐漸增大。

（2）碳交易政策的實施有利于降低碳排放強度，且政策影響同樣逐年增大，與該政策對碳排放量的影響相比，相關系數明顯更大。

（3）在對碳排放量和碳排放強度的影響過程中，經濟水平和技術水平等因素的影響效果比較顯著，而產業結構和人口規模等變量到目前為止尚未表現出明顯影響；特別地，我國二氧化碳排放量與經濟發展水平之間滿足EKC假說，二者之間存在倒“U”形曲線關系。

（4）采用多時點雙重差分法評估碳交易政策的有效性滿足該方法的前提條件：政策的干預時間具有隨機性，處理組的選擇具有隨機性，控制組不受政策影響，且處理組和控制組在政策發生前具有共同趨勢。

基于以上研究結論，本文提出建議：

（1）碳交易政策實行以來，其對于減少碳排放量和降低碳排放強度的效果顯著，具有將其推廣到全國范圍的理論和實證基礎。中央和地方相關部門可以結合全國和各省份具體情況，參考歐盟、澳大利亞等國際碳交易市場和北京、天津等國內碳交易試點省區的相關經驗，綜合考慮推廣實施碳交易政策的具體辦法，因地制宜，科學規劃，最大限度地發揮碳交易政策的減排效果。

（2）提高經濟發展水平和科技水平是減少二氧化碳排放量和降低二氧化碳排放強度的重要途徑，不斷提高技術水平，進一步推動經濟高質量發展，盡早實現經濟發展水平與碳排放量的倒“U”形拐點的到來。

參考文獻：

[1]DUMAN Y S， KASMAN A. Environmental technical efficiency in EU member and candidate countries： A parametric hyperbolic distance function approach[J]. Energy， 2018， 147： 297-307.

[2]劉傳明，孫喆，張瑾.中國碳排放權交易試點的碳減排政策效應研究[J].中國人口·資源與環境，2019，29（11）：49-58.

[3]路正南，羅雨森.中國碳交易政策的減排有效性分析——雙重差分法的應用與檢驗[J].干旱區資源與環境，2020，34（4）：1-7.

[4]王勇，趙晗.中國碳交易市場啟動對地區碳排放效率的影響[J].中國人口·資源與環境，2019，29（1）：50-58.

[5]任亞運，傅京燕.碳交易的減排及綠色發展效應研究[J].中國人口·資源與環境，2019，29（5）：11-20.

[6]宋德勇，易艷春.外商直接投資與中國碳排放[J].中國人口·資源與環境，2011，21（1）：49-52.

[7]CHRISTOPH B， WELSCH H. Contraction and convergence of Carbon emissions： an intertemporal multi-region CGE analysis[J]. Journal of Policy Modeling， 2004， 26（1）： 21-39.

[8]孫睿，況丹，常冬勤.碳交易的“能源—經濟—環境”影響及碳價合理區間測算[J].中國人口資源與環境，2014，24（7）：82-90.

[9]譚秀杰，劉宇，王毅.湖北碳交易試點的經濟環境影響研究——基于中國多區域一般均衡模型TermCO2[J].武漢大學學報（哲學社會科學版），2016，69（2）：64-72.

[10]湯鈴，武佳倩，戴偉，等.碳交易機制對中國經濟與環境的影響[J].系統工程學報，2014，29（5）：701-712.

[11]陳醒，徐晉濤.中國碳交易試點運行進展總結[A].薛進軍，趙忠秀，戴彥德，等.中國低碳經濟發展報告（2017）[C].北京：社會科學文獻出版社， 2018.

[12]范丹，王維國，梁佩鳳.中國碳排放交易權機制的政策效果分析——基于雙重差分模型的估計[J].中國環境科學，2017，37（6）：2383-2392.

[13]馬曉偉，余華銀.碳排放權交易政策對環境效率影響的實證研究[J].荊楚理工學院學報，2019，34（2）：88-96.

[14]仲云云，仲偉周.我國碳排放的區域差異及驅動因素分析——基于脫鉤和三層完全分解模型的實證研究[J].財經研究，2012，38（2）：123-133.

[15] WU L B， KANEKO S， MATSUOKA S. Driving forces behind the stagnancy of Chinas energy-related CO2emissions from 1996 to 1999： the relative importance of structural change， intensity change and scale change[J]. Energy Policy， 2005， 33（3）： 319-335.

[16]雷厲，仲云云，袁曉玲.中國區域碳排放的因素分解模型及實證分析[J].當代經濟科學，2011，33（5）：59-65，126.

[17]涂正革，諶仁俊，韓生貴.中國區域二氧化碳排放增長的驅動因素——工業化、城鎮化發展的視角[J].華中師范大學學報（人文社會科學版），2015，54（1）：46-59.

[18]郭朝先.產業結構變動對中國碳排放的影響[J].中國人口·資源與環境，2012，22（7）：15-20.

[19]田立新，張蓓蓓.中國碳排放變動的因素分解分析[J].中國人口·資源與環境，2011，21（11）：1-7.

[20] REN S G， YIN H Y， CHEN X H. Using LMDI to analyze the decouplingofCarbondioxideemissionsbyChinas manufacturing industry[J]. Environmental Development， 2014， 9： 61-75.

[21]鄧吉祥，劉曉，王錚.中國碳排放的區域差異及演變特征分析與因素分解[J].自然資源學報，2014，29（2）：189-200.

[22]王菲，楊雪，田陽，等.基于EKC假說的碳排放與經濟增長關系實證研究[J].生態經濟，2018，34（10）：19-23.

[23]劉穎，任燕燕.基于VEC模型的中國CO2庫茲涅茨曲線分析[J].安徽師范大學學報（人文社會科學版），2012，40（1）：25-30.

[24]劉華軍，閆慶悅，孫曰瑤.中國二氧化碳排放的環境庫茲涅茨曲線——基于時間序列與面板數據的經驗估計[J].中國科技論壇，2011（4）：108-113.

[25]陳林，伍海軍.國內雙重差分法的研究現狀與潛在問題[J].數量經濟技術經濟研究，2015，32（7）：133-148.

[26]周晶，陳玉萍，丁士軍.“一攬子”補貼政策對中國生豬養殖規模化進程的影響——基于雙重差分方法的估計[J].中國農村經濟，2015（4）：29-43.

Carbon Trading Policy and Carbon Emission： An Empirical Test of Time-Varying DID Model

LI Yanqin，LI Zongyao，ZHANG Qian

（Party School Of C.P.C. Jiangsu Committee， Nanjing 210009，China）

Abstract： Based on the coase theorem， this paper established a time-varying DID model of carbon emission and carbon emission intensity， and conducted empirical test on the panel data of 30 Chinese provincial administrative regions（excluding Hong Kong， Macao， Taiwan and Tibet autonomous region） from 2007 to 2017 to investigate the impact of carbon trading policies on carbon emissions.The time-varyingDID results show that the carbon trading policy has a significant promoting effect on the reduction of carbon emissions.The implementation of carbon trading policy is conducive to the reduction of carbon emission intensity， and the impact of the policy is also increasing year by year. In the process of influencing carbon emission and carbon emission intensity， factors such as economic level and technological level have a significant effect， while variables such as industrial structure and population size have not yet shown significant influence；In particular， Chinas carbon dioxide emissions and economic development level meet the EKC hypothesis， and there is an inverted "U" curve relationship between them.

Keywords： carbon trading；carbon emissions；carbon emission intensity；Time-varying DID model