探究性教學在三角函數教學中的應用
陳金城
(甘肅省合水縣第一中學 745400)
一、培養學生動手探究熱情
數學學科與人們的日常生活有十分緊密關聯,其是對生活的高度總結,同時又為生活所提供服務.三角函數知識也是這樣,在現實生活中,有很多方面都體現出了三角函數的知識點,如時鐘指針轉動方向、風暴運動軌跡測量等,因此在三角函數教學中,教師可以從學生的現實生活出發,為學生創建生活化情境,指引學生借助現實生活來探索三角函數內容,調動學生的探究積極性.例如教師在引導學生學習“任意角的三角函數”這部分內容時,教師可以利用多媒體為學生展示這樣的情景:有一個半徑是30m的圓形廣場,廣場正中央有一個探照燈,照向地面的光柱呈現圓錐形,其軸截面的頂角時120°,如果這一光源正好照亮整個廣場,那么探照燈距離地面的高度應該是多高?教師通過為學生設置這樣探究性的生活問題,可以顯著激發學生的探究欲望,學生的學習效果也會因此而提高.
二、引導學生自主探究能力
對于數學知識,其本身具有很強的系統性、邏輯性、縝密性,其在培養學生邏輯思維能力上具有良好的作用.在高中數學三角函數一章,學生要掌握的知識點有很多,學生要想獲得良好的學習效果,就需要對三角函數章節知識的內在聯系、整體結構有準確、全面的了解,這樣才能為學生的學習打下良好基礎.因此,在實踐中,高中數學教師必須注重對學生進行引導,充分發揮出學生的自主性,指引學生能通過自主探究、合作交流的方式完成三角函數知識整理,促進學生完整知識鏈的形成.學生在自主探究三角函數的知識點時,發現知識點有很多,如正余弦函數、正切函數的誘導公式、函數圖象及性質等,學生經過系統的整理,會形成一個結構清晰的知識網絡圖,這樣學生在處理三角函數的問題時會更加輕松.
三、強化學生實際問題解決能力
與其他學科一樣,數學學科的落腳點也是引導學生進行知識實踐,因此,在高中數學三角函數知識講解中,教師也需要引導學生在探究中提高自身的實際問題解決能力,這樣才能促進學生數學核心素養的提高.學生在學習中,掌握了三角函數圖象平移規律、伸縮規律,三角函數最值求解等知識后,教師要引導學生靈活地應用換元法、待定系數法、坐標法、轉化思想等解決三角函數問題,以此促進學生綜合發展.
例如,某港口水的深度是y,與時間t成函數關系y=f(x)(0≤t≤24),對該港口水位數據進行測量,發現在0、3、6、9、12、15、18、21、24時,水位深度分別是10.0m、13.0m、10.01m、7.0m、10.0m、13.0m、7.0m、10.0m.經過長期觀察,發現函數y=f(x)的圖象可以近似看作y=Asinωt+b的圖象.船在航行的時候,船底距離海底的距離不低于5m則表示船出行是安全的,某船吃水深度(船底與水面的距離)在6.5m,如果希望該船可以在一天內進出港,則在港內停留的時間是多少?
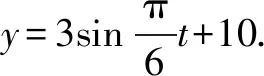
通過這樣的實際問題探究,不僅可以全面加深學生對于三角函數知識的理解,同時還可以促進學生解題能力的提升.
四、通過對比探究本質
由于三角函數的部分公式、例題形式都比較相似,因此教師在可以引導學生對這些公式、例題進行對比,在對比中幫助學生把握本質,促進學生探究水平的提升.例如公式sin(A+B)=sinAcosB+cosAsinB,sin(A-B)=sinAcosB-cosAsinB,cos(A+B)=cosAcosB-sinAsinB,cos(A-B)=cosAcosB+sinAsinB在形式上十分相似,因此,教師可以組織學生對這幾個公式進行對比、分析,讓學生總結出這些公式的特點,如sin公式前后符號是相同的,但是等式右邊是“不同±不同”的形式,而cos公式前后符號不同,右邊形式則是“相同?相同”.通過這樣的對比,學生對于這部分知識就會有全面的了解.
總而言之,三角函數是高中數學十分重要的內容,由于三角函數知識內容相對比較特殊,學生在學習過程中會感覺十分困難,因此教師要采取多樣化的教學手段,引導學生可以靈活地應用學到的知識來探究、解決三角函數問題,促進學生的良好發展.

