隔離非線性分層殼有限單元法

李 鋼，呂志超，余丁浩

(大連理工大學海岸和近海工程國家重點實驗室，遼寧，大連 116024)

板殼單元作為數值計算分析中常見的單元類型，被廣泛應用于建筑和橋梁等結構的數值模擬中[1―3]。多年來，國內外研究學者對板殼單元的計算精度和非線性求解效率兩方面做了大量研究[4―5]。目前，板單元主要有兩種分析理論，一種是Kirchhoff板理論[6]，該理論假定撓度和轉角相互獨立且要求位移為C1類連續，主要適用于由薄板組成的工程結構中[7-9]，但當板厚增加時，該理論模擬結果的精度降低甚至會導致錯誤的計算結果；另一種理論是Mindlin-Reissner中厚板理論[10-11]，該理論克服了Kirchhoff板理論的不足，在解決中厚板問題上具有足夠的精度，被廣泛應用于結構有限元非線性分析中[12-15]。針對殼單元，其理論通常包括三種：由平面膜單元和板彎曲單元組成的平板型殼元[16]、經典的曲面型殼元[17]以及三維實體退化型殼元[18]，其中，曲面型殼元和退化型殼元的有限元列式比較復雜且收斂性較差，在實際應用中難以實施。而平板型殼元具有構造簡單、計算精度高等優點，被廣泛應用于實際工程中[19]。近年，隨著復合材料層合板殼結構的出現，單一材料的板殼單元已經無法滿足工程應用需要[20-21]。因此，研究人員以復合材料力學原理和平板型殼元基本理論為基礎，開發了一種分層殼單元模型，該模型將不同的材料本構行為聯系起來，在模擬實際構件或者結構復雜受力方面具有明顯優勢。陸新征等[22]和張有佳等[23]將分層殼模型應用于鋼筋混凝土剪力墻和核電預應力混凝土安全殼的非線性分析中，研究結果均表明該模型具有良好的計算精度。

在板、殼單元模型的非線性計算方面，高效的數值求解方法同樣占據重要地位。Farhat和Wilson[24]、楊玉明[25]將基于預處理共軛梯度法的并行計算方法應用于板殼結構的非線性分析中，大大提高了板殼結構的并行計算效率。Li、Carrera等[26]提出一種分層殼有限元模型自適應方法，提高了分層殼結構的有限元非線性數值分析效率。盡管學者們提出的數值求解方法在很大程度上改善了板、殼單元的計算效率，但在非線性分析時仍需要對切線剛度矩陣進行合成和分解，該過程將消耗大量的計算資源。

隔離非線性有限元法[27]作為一種結構非線性分析新方法，將結構的非線性部分隔離開來，并將結構的切線剛度矩陣的逆矩陣表示成初始彈性剛度矩陣的逆與相應修正矩陣的和，從而避免了切線剛度矩陣的直接分解，實現了非線性問題的高效求解。目前，該方法已被應用于平面單元、纖維梁單元的材料非線性分析中[28]。而分層殼單元作為建筑結構數值模擬的重要組成部分，有必要建立基于隔離非線性有限元法的分層殼單元分析模型，對提高板殼單元非線性分析效率具有較大意義。本文根據隔離非線性有限元法和分層殼單元理論，將單元截面變形分解為線彈性變形和非線性變形，以高斯積分點作為非線性變形插值結點，建立了非線性變形場。依據虛功原理和積分點處的內力平衡條件建立了基于隔離非線性有限元法的分層殼單元控制方程，采用Woodbury公式和組合近似法聯合求解控制方程。基于時間復雜度理論對模型的計算效率進行評價，結果表明：隔離非線性有限元法的分層殼單元模型相比于傳統有限元方法的模型計算效率顯著提高，數值算例驗證了本文單元模型的準確性與高效性。

1 基本理論

1.1 分層殼單元

分層殼單元基于復合材料力學原理，將一個殼單元沿厚度方向上劃分成若干層，各層可根據需要設置不同的厚度和材料，每一層由平板型殼單元組成，如圖1所示。分層殼單元考慮了面內應變—面外彎曲之間的耦合作用，能較全面地反映殼體結構的空間力學性能[29]。

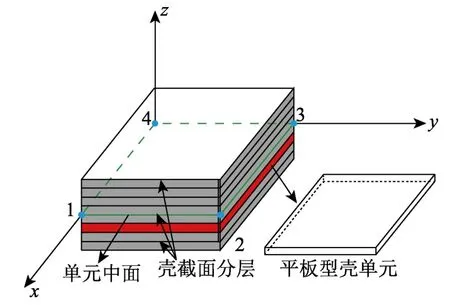
圖1 分層殼單元示意圖Fig.1 Sketch of multi-layer shell elements

以常用的四節點平板型分層殼單元為例，對其基本理論和公式進行闡述，如圖2所示。單元中面設置4個位移插值結點，每個位移插值結點有6個自由度，其結點位移增量可用列陣表示為[30-31]：

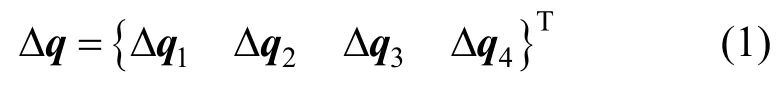
式中：Δqi={ΔuiΔviΔwiΔθxiΔθyiΔθzi}T，其中，Δui、Δvi、Δwi分別為沿x、y及z軸方向的平動位移增量，Δθxi、Δθyi、Δθzi分別為繞x、y及z軸的轉角位移增量。平板型分層殼單元面內和面外的變形行為可分別通過平面膜單元和板彎曲單元來進行模擬，其中平面膜單元提供面內位移以及面內轉動的分量，即板彎曲單元則提供面外撓度及繞x、y軸轉角的分量，其節點位移分量表示為

圖2 四結點平板型分層殼單元Fig.2 Sketch of flat multi-layer shell element with four nodes

依據單元沿厚度方向的平截面假定，通過單元中面的任意一點的位移和橫截面上的轉角，可得單元內任意一點的位移場增量方程，具體可表示為：

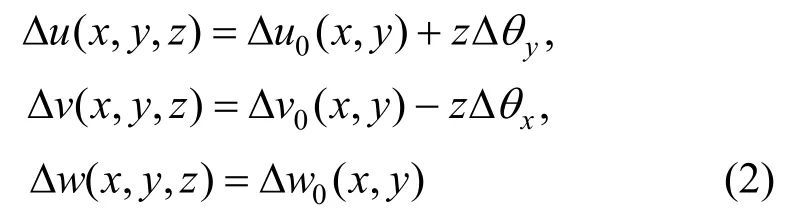
式中：Δu0、Δv0、Δw0為單元中面任意一點的位移增量；z為分層殼單元任意層與中面的距離。由彈性力學的幾何方程可知，對式(2)求一階偏導數可得到單元中面的應變和曲率增量，即：

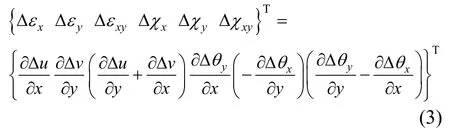
式中：Δεx、Δεy分別為x和y方向應變增量；Δεxy為面內剪切應變增量；Δχx、Δχy分別為分層殼單元中面的x和y方向曲率增量；Δχxy為中面扭轉率增量。為下文表述方便，令Δdm={ΔεxΔεyΔεxy}T為膜單元變形場，Δdb={ΔχxΔχyΔχxy}T為板元彎曲變形場。

得到單元中面的應變和曲率后，根據各層材料之間滿足平截面假定和各層在橫截面上的坐標，可計算出各層的應變，分層殼單元第j層的應變增量可表示為：

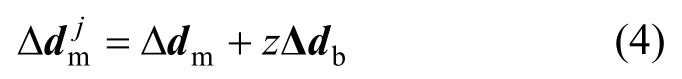
在面外荷載作用下，分層殼單元在厚度方向上通常發生面外剪切變形，而單元厚度變薄將會發生剪切閉鎖現象，為解決該問題，學者采用假設剪應變法計算面外剪切應變，其基本原理是：單元內的剪切應變由插值點處的剪切應變按線性插值表示，則單元的剪切應變增量Δγxz、Δγyz可具體表示為[32]：

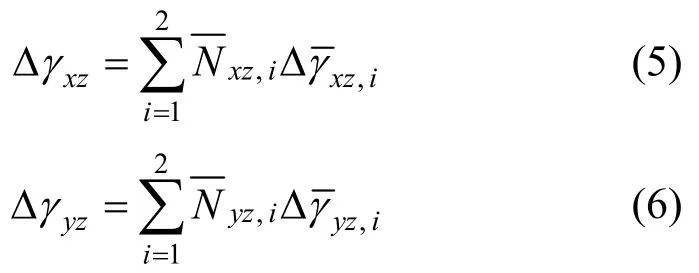
設單元截面變形增量分布函數為：

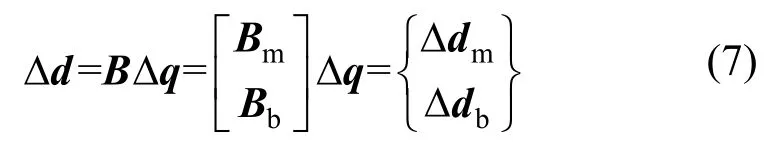
式中：Δd={ΔdmΔdb}T為截面變形向量；B=[BmBb]T為單元的變形矩陣；Bm和Bb分別為膜單元和板彎曲單元變形矩陣。

2.2 截面變形分解

隔離非線性方法作為一種高效的非線性求解方法[27]，是將材料本構關系中的應變分解為線彈性和非線性兩部分，如圖3所示。

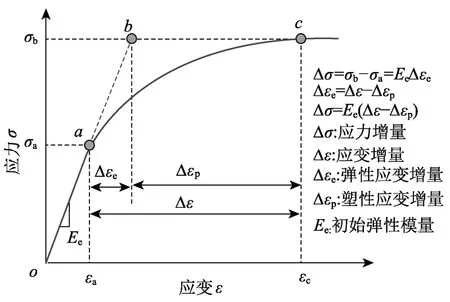
圖3 應變分解Fig.3 Strain decomposition of material

當采用分層殼單元計算材料非線性問題時，可基于隔離非線性的思想，將分層殼單元截面變形分解為線彈性及非線性兩部分。由于面外剪切變形對單元非線性行為影響較小，在此不考慮面外剪切變形的非線性，認為其一直處于彈性狀態，單元的膜單元變形和板元彎曲變形可分解為：

式中：Δde={Δdm,eΔdb,e}T為截面線彈性變形增量；Δdp={Δdm,pΔdb,p}T為截面非線性變形增量。

在截面內力計算方面，分層殼第j層的應力增量可通過該層的剛度矩陣和應變增量相乘得到，對截面中各層的應力增量進行積分，得到膜內力增量和彎矩增量，具體表達式為：

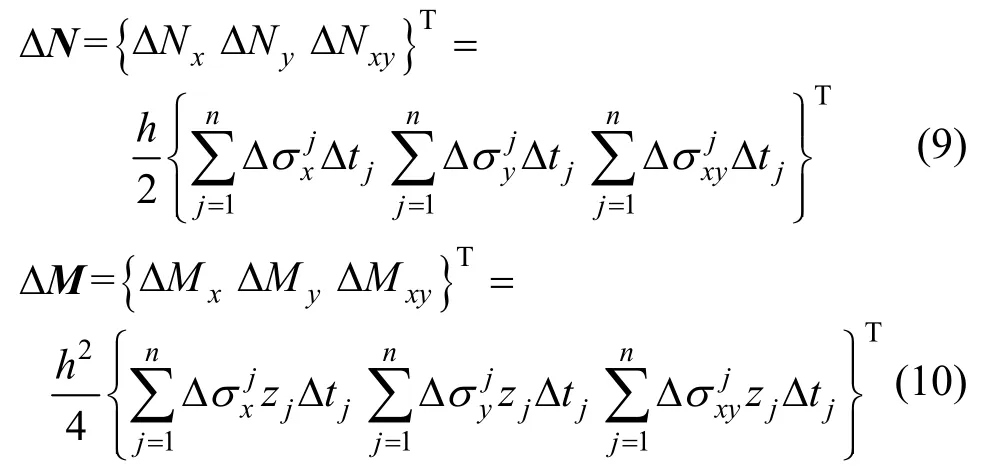
由圖3可知，材料的應力等于彈性應變和彈性模量的乘積，而分層殼單元中截面的內力可通過截面彈性變形與截面彈性剛度矩陣相乘得到，結合式(8)截面變形的分解，截面內力的表達式為：

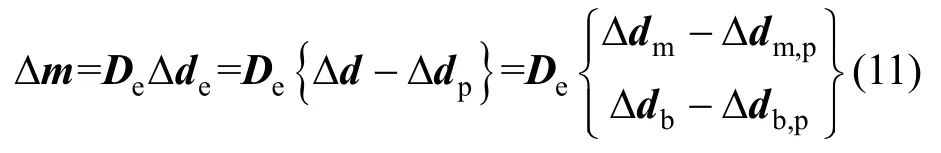
式中：Δm={ΔNΔM}T為截面內力；De=為彈性剛度矩陣；為膜單元應力狀態下的第j層彈性剛度矩陣。

由式(11)可知，基于截面變形分解的方法求解截面內力時，引入了未知量Δdp，依據有限元基本理論：單元的變形場增量Δd可通過變形插值函數和結點位移增量表示，同樣Δdp可通過非線性變形插值結點處的非線性變形增量Δdp進行插值得到[28]，即：

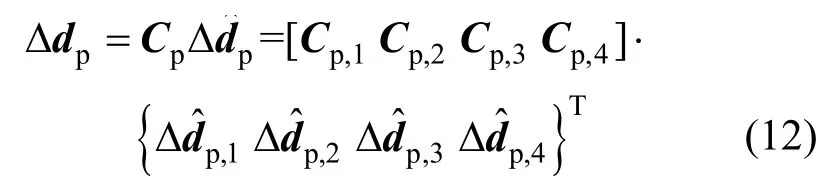
在傳統變剛度有限元方法的非線性求解迭代過程中，截面內力增量線性化表達式還可表示為[31]：

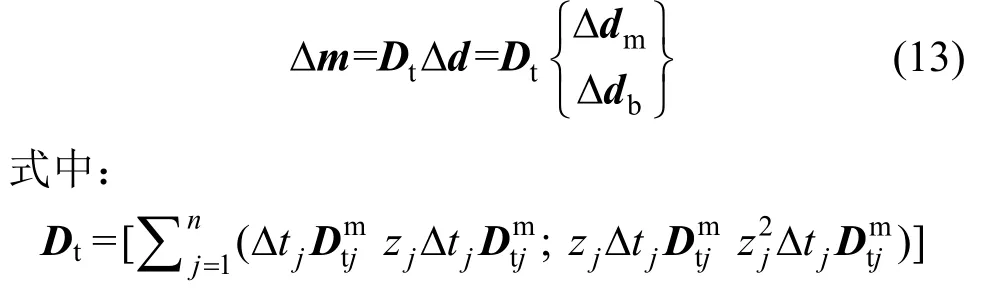
為切線剛度矩陣，為膜單元應力狀態下的第j層的切線剛度矩陣。對比式(11)和式(13)可知：在非線性分析過程中，基于變形分解的截面內力表達式可以保證截面剛度矩陣的始終不變。

3 隔離非線性分層殼控制方程

根據虛功原理，分層殼單元變分表達式為：

式中：δd為截面變形的變分；δq為單元節點位移的變分；Δf為單元節點力增量。將式(7)、式(8)、式(11)和式(12)代入虛功方程式(14)，經整理可得：

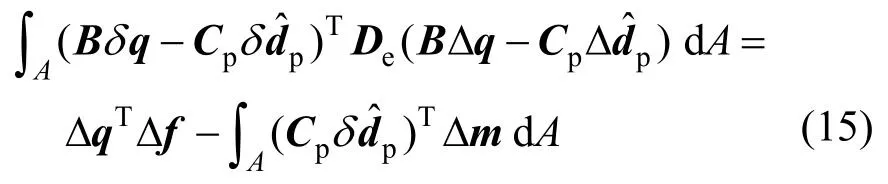
此外，考慮塑性插值點處的內力平衡條件，將式(11)和式(12)代入式(13)可得補充方程：

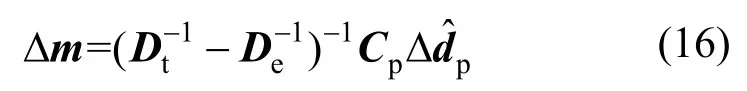
將式(16)代入式(15)，經整理可得基于隔離非線性方法的分層殼單元控制方程：

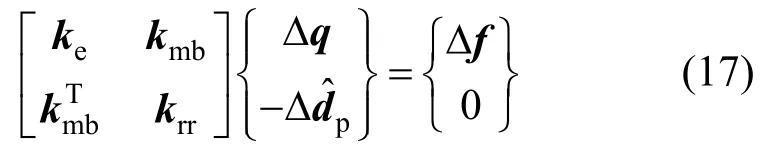
式中：ke為單元初始彈性剛度矩陣；kmb表示非線性變形與單元節點力之間的關系；krr為單元的非線性矩陣，表示了單元的非線性信息。其具體表達式分別如下：

對單元控制方程集成，得到結構的整體控制方程：

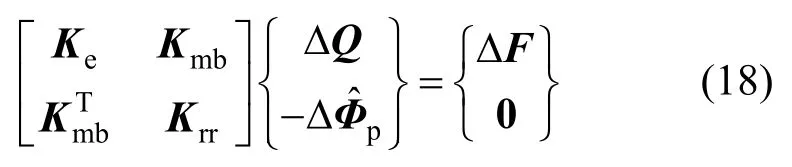
式中：ΔQ為結構的位移向量；ΔF為結構的荷載向量；為結構中所有塑性插值點處的非線性變形向量。矩陣Krr為分塊對角矩陣，每個塊矩陣表示了每個高斯積分點的材料非線性信息，若該高斯積分點沒有進入非線性，則該塊矩陣為零矩陣。在非線性分析過程中，只更新和分解矩陣Krr，矩陣Ke和Kmb均為常數矩陣且與材料非線性狀態無關。

4 控制方程求解

在結構非線性分析任意迭代步內，可利用Woodbury公式對結構的整體控制方程式(18)進行準確和高效的求解。其求解高效性主要體現為：在局部非線性分析過程中，結構中的大部分單元一般處于線彈性狀態，僅有小部分單元進入非線性，因而，進入非線性的塑性自由度數p遠小于結構位移自由度數n(p＜＜n)，在迭代步內僅需對p維的矩陣合成和分解，避免了對n維整體剛度矩陣實時更新和分解，降低了結構非線性分析的計算時間。而傳統變剛度有限元分析中，大部分計算時間消耗在n維切線剛度矩陣的分解上。

基于此，采用Woodbury公式求解整體控制方程式(18)，其展開形式為：

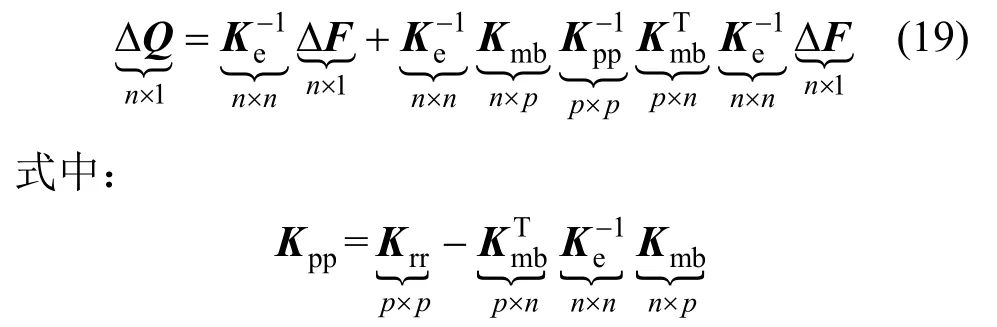
在數學上，矩陣Kpp稱為整體剛度矩陣Ke的舒爾補，其矩陣維數為p×p階，與塑性自由度數目一致[27]。從式(19)可知：Woodbury公式求解整體控制方程時，其計算量主要來自舒爾補矩陣Kpp的實時更新和分解，因而，非線性分析過程中產生塑性自由度數的多少直接影響著Woodbury公式的計算效率。以往的研究表明[33-34]：當結構局部進入材料非線性時，Woodbury公式求解效率比傳統有限元方法求解效率高，對于一個位移自由度n=10000的結構，當進入塑性的塑性自由度數p≥1000時，Woodbury公式求解效率低于傳統有限元方法。

4.1 Woodbury公式和CA法聯合求解

在板殼單元的非線性分析中，由于單元和其周圍單元聯系緊密，單元與單元之間的高斯積分點相互之間影響較大，即使在局部材料非線性階段，進入非線性的塑性自由度數也較多，所以使用Woodbury公式求解整體控制方程在板殼單元非線性分析中存在一定的局限性。組合近似法(combined approximations method， CA法)通過構造s個線性無關的基向量來線性逼近位移向量[35]，由于基向量個數s比結構位移自由度數n小很多，所以大幅度的減小了非線性分析過程中的計算量。把式(19)的求解過程具體分解為從右至左的6個計算步驟，其計算過程如圖4(a)所示，由Woodbury公式求解分析可知，較大維數的矩陣Kpp直接分解計算是影響基于隔離非線性有限元法的板殼單元求解效率的關鍵因素，當采用CA法求解圖4(a)中的步驟③時，在非線性求解過程中主要是矩陣回代與向量之間的運算，避免了矩陣Kpp的直接分解計算，提高了基于隔離非線性有限元法的板殼單元的計算效率。CA法求解步驟③的具體計算過程如圖4(b)所示，圖4表示了結構非線性分析過程中一個迭代步內的完整計算。

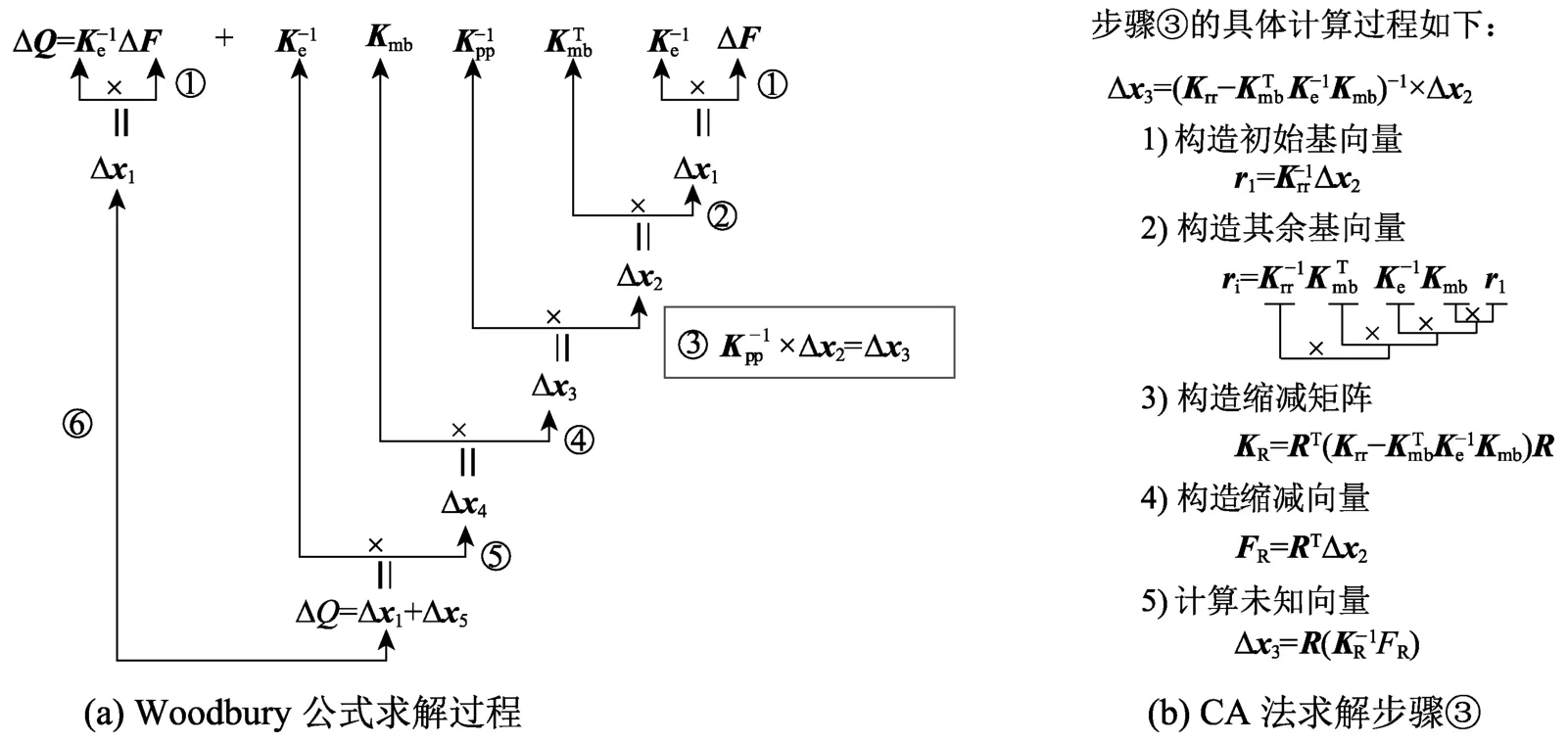
圖4 Woodbury公式和CA法聯合求解過程示意圖Fig.4 Sketch of Woodbury formula and CA method solving process

4.2 效率分析

時間復雜度理論[33]是一種算法計算效率定量評價的方法，僅與算法本身相關，與硬件、軟件、編程語言以及程序優化等因素無關。傳統有限元方法在增量步內的每個迭代步的計算過程中都需要對規模為n×n階、帶寬為m階的整體剛度矩陣進行一次LDLT分解，一次分解和回代的時間復雜度函數為[34]：

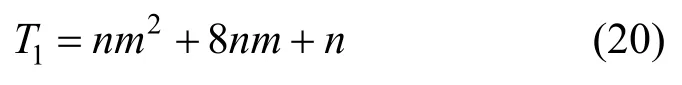
Woodbury公式和CA法聯合求解整體控制方程時，只需要在開始計算前對規模為n×n階、帶寬為m階的剛度矩陣Ke進行一次LDLT分解。根據圖4所示的求解過程，通過對Woodbury公式和CA法聯合求解整體控制方程的計算量進行統計，其時間復雜度函數約為[36]：

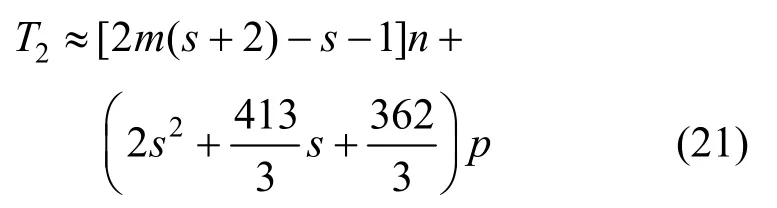
式中：m為剛度矩陣的帶寬，一般可取為s為基向量個數；p為進入塑性的塑性自由度數。

5 數值算例

5.1 空心板

板的幾何尺寸及構造如圖5所示，邊長為2000 mm×2000 mm，厚度為30 mm，板的四周為固定支座。將板模型劃分為400個單元，在厚度方向上每個單元劃分20層，其中在單元中面的上、下兩層為空心層。板上承受均布荷載q=6.25 N/mm2，總計1251個增量步，力加載曲線如圖6所示。彈性模量為E=2×105MPa，泊松比為ν=0.3，屈服強度為262 MPa，屈服后剛度系數為0.1。模型位移自由度總數為1323，每個單元有12個塑性自由度，塑性自由度總數為4800。

分別采用有限元軟件ANSYS和隔離非線性有限元法建立分析模型，兩種方法的單元數量、截面劃分的層數和材料本構關系均相同，其中，ANSYS模型中的單元類型為shell181單元，與隔離非線性有限元法中使用的分層殼單元類型相同。圖7(a)和圖7(b)分別給出了板中心點A的撓度-荷載曲線和第80個單元的1節點x方向的應力-應變曲線對比圖，可知：隔離非線性有限元法的計算結果與ANSYS的計算結果吻合較好，驗證了隔離非線性分層殼有限元法的準確性。

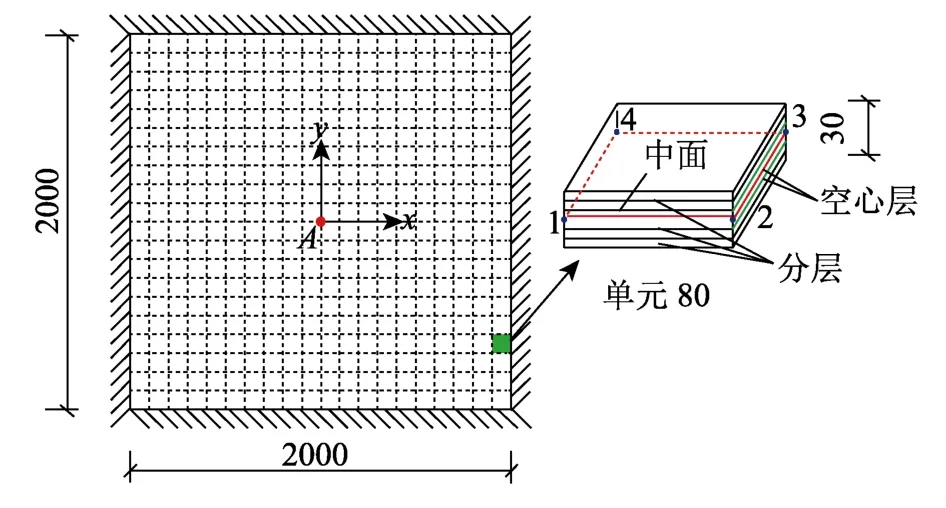
圖5 模型尺寸及分層 /mmFig.5 Size and layers of the model structure

圖6 力加載曲線Fig.6 Force loading curve

圖8給出了加載過程中板進入非線性狀態的塑性自由度數量演變曲線，其中最大的塑性自由度數是4764，平均塑性自由度數是2498(位移自由度總數的187.96%)，表明了結構發生了很大范圍的材料非線性變形，同時，板中進入非線性狀態的塑性自由度數隨著外荷載和加卸載條件的改變而動態變化。傳統變剛度有限元方法和隔離非線性有限元法的時間復雜度曲線如圖9所示，可知：有限元方法的時間復雜度保持不變，且僅與結構位移自由度有關，而隔離非線性有限元法的時間復雜度與結構自由度及產生的塑性自由度數均相關。對于大范圍的材料非線性問題，即板中所有單元全部進入非線性狀態，隔離非線性有限元法的時間復雜度也是低于傳統有限元方法的，表明本文方法提高了分層殼單元在非線性分析過程中的數值計算效率。

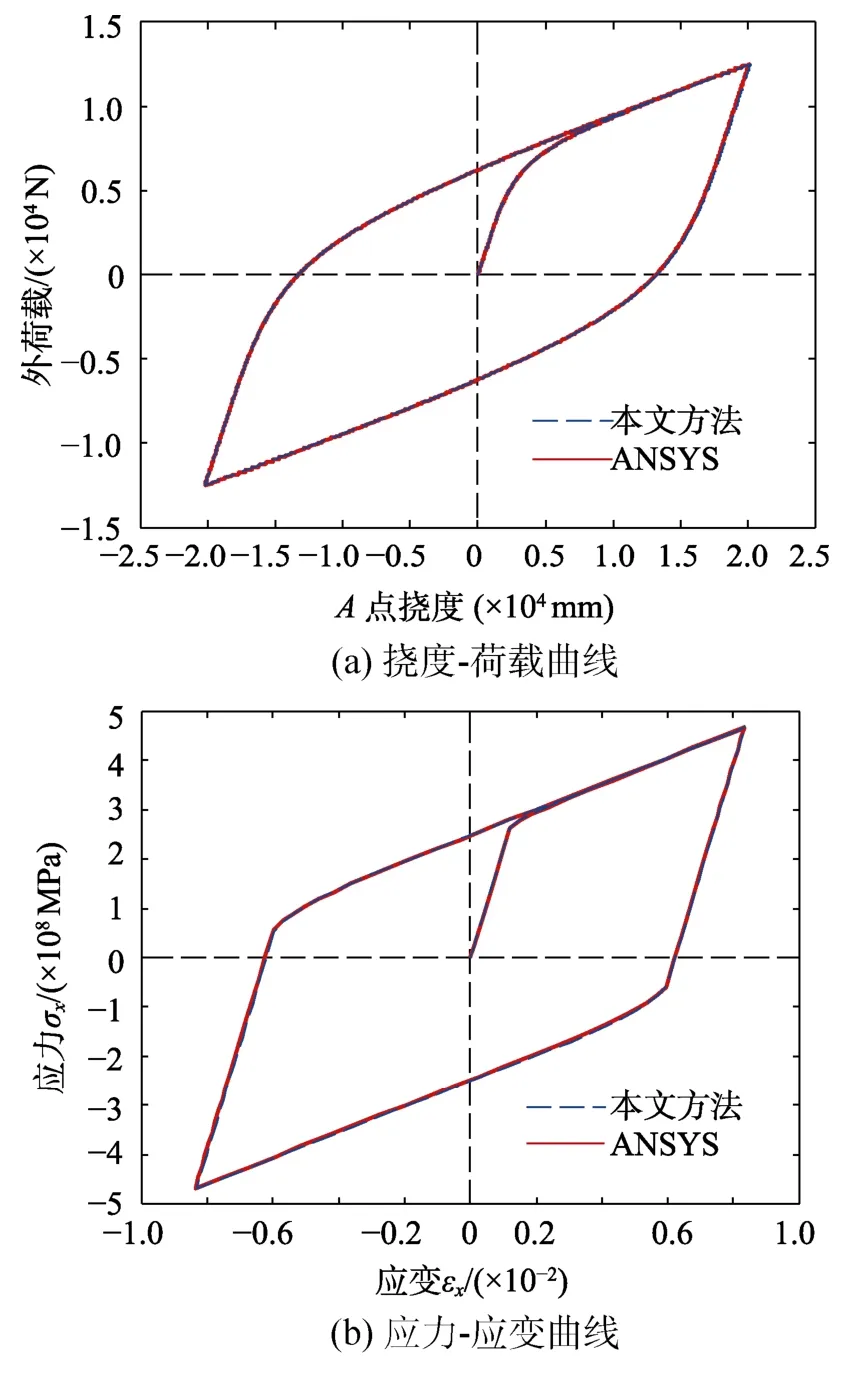
圖7 結果曲線對比Fig.7 The comparison curve of the results

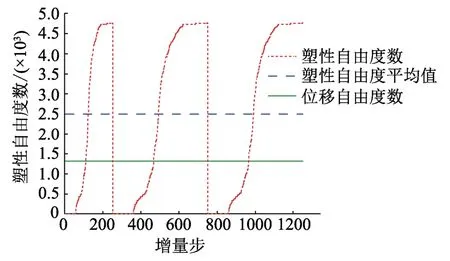
圖8 塑性自由度Fig.8 Plastic degree of freedoms

5.2 剪力墻

圖10為某一單片鋼板剪力墻，墻底部與基礎固結，墻的寬度為1000 mm、高度為2000 mm，將墻劃分為40個單元，每個單元截面在厚度方向上為100 mm并劃分為10層。在節點16施加x、y和z三個方向的荷載，大小均為Fx=Fy=Fz=336000 N，力控制加載，總計500個增量步。材料本構關系采用理想彈塑性本構模型，屈服強度為235 MPa，彈性模量為E=2.1×105MPa，泊松比為ν= 0.3。塑性自由度個數為960，位移自由度個數為330。

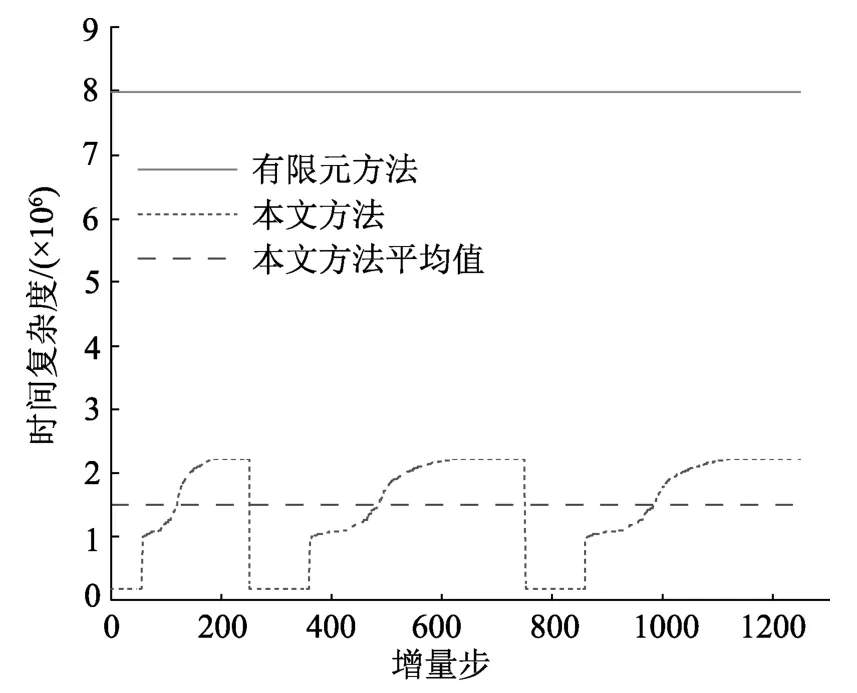
圖9 時間復雜度理論Fig.9 The comparison of time complexity theory

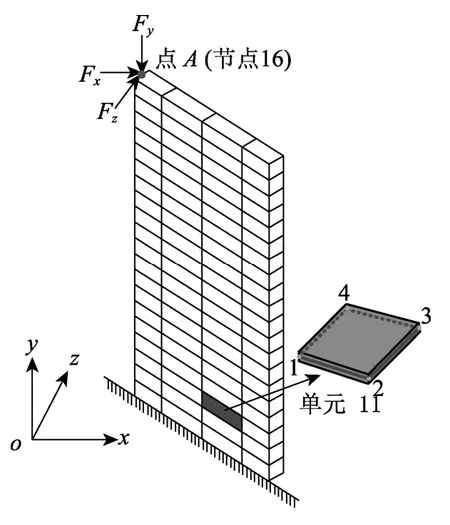
圖10 剪力墻模型Fig.10 The model of shear wall

分別采用有限元軟件ANSYS和隔離非線性有限元法建立分析模型。圖11給出了使用隔離非線性有限元法和傳統有限元方法計算得到的加載點A的x、y和z三個方向的位移-荷載(F-u)曲線，從圖中可知三個方向的位移吻合良好，因為剪力墻的面內剛度大于面外剛度，所以z方向的位移進入非線性程度較強，x、y方向的位移進入非線性程度較弱，表明：剪力墻三個方向相互之間的耦合受力減低了剪力墻的承載能力。圖12給出了使用兩種方法得到的單元11中3節點的應變和應力曲線對比圖，可知：單元的應變和應力變化趨勢及計算精度與傳統有限元方法的基本相同，驗證了本文提出分層殼單元模型的準確性。

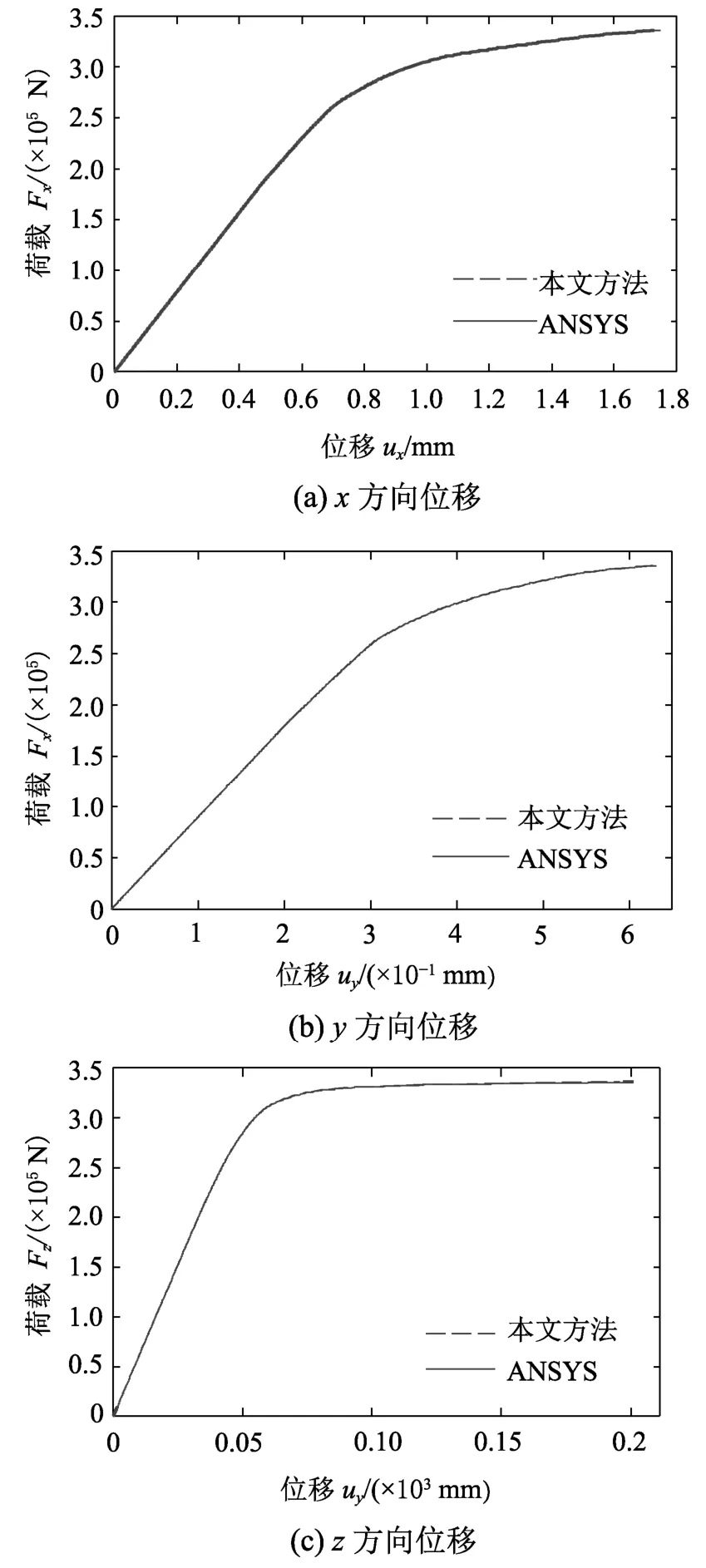
圖11 位移曲線Fig.11 The comparison of displacement curve

圖13給出了塑性自由度數隨增量步的變化曲線，非線性分析過程中產生的最大塑性自由度數為252，占總自由度數的76.36%，而每個增量步的平均塑性自由度數為129，占總自由度數的39.1%，表明結構較大范圍的出現材料非線性。為論證其高效性，將傳統有限元方法和本文方法的時間復雜度進行統計對比，如圖14所示，傳統有限元法和本文方法的平均時間復雜度分別為5.588×105和1.004×105，此外，傳統有限元法的時間復雜度為本文方法的5.57倍，表明本文方法能夠高效地求解結構復雜受力狀態下的大范圍材料非線性問題。

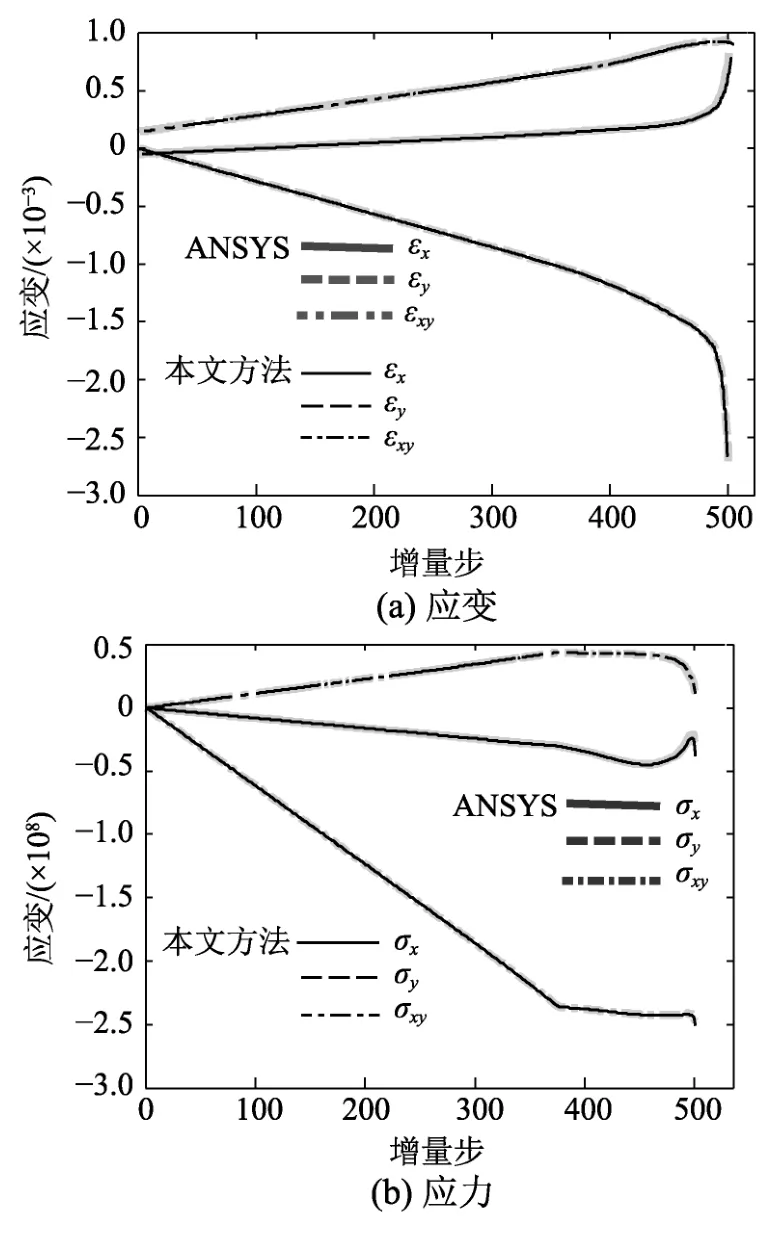
圖12 應變-應力曲線Fig.12 The comparison of stress-strain

圖13 塑性自由度Fig.13 Plastic freedoms degree

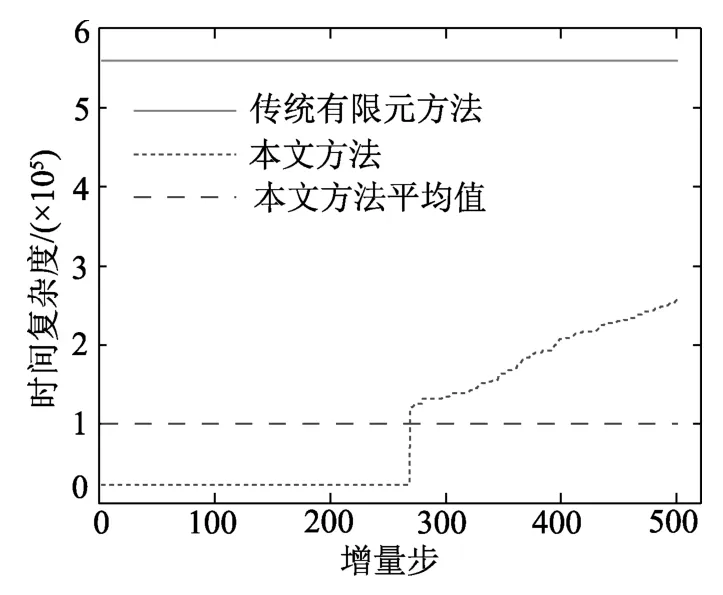
圖14 時間復雜度理論Fig.14 The curve of time complexity theory

6 結論

本文基于隔離非線性有限元法和分層殼單元的基本理論，將單元截面變形分解為線彈性及非線性兩部分，推導了分層殼單元的隔離非線性控制方程，聯合Woodbury公式和CA法對控制方程進行高效求解。最后，將該方法應用于板、剪力墻結構與構件的非線性分析中，并得到如下結論：

(1) 與傳統的分層殼單元有限元模型相比，本文方法可保證單元初始剛度矩陣保持不變，將單元材料非線性集中于控制方程的右下角矩陣塊中，實現了單元非線性性狀態的隔離。

(2) 依據時間復雜度理論分析可知，隔離非線性有限元法的分層殼單元模型與傳統有限元方法相比，即使結構大范圍出現材料非線性行為時，本文方法也可顯著提高分層殼單元的非線性求解效率。

(3) 通過與有限元軟件ANSYS的結果對比分析表明，本文方法與傳統有限元方法在求解分層殼單元的材料非線性問題時具有一致的計算精度。