考慮行波效應(yīng)的大跨度矮塔斜拉橋耐震時程分析

沈 禹，談華順，王獻摯，李建中

(1.同濟大學(xué)土木工程防災(zāi)國家重點實驗室，上海 200092；2.浙江省交通規(guī)劃設(shè)計研究院有限公司，浙江，杭州 310006)

我國中西部地區(qū)地形和地貌復(fù)雜，交通線路常需橋梁結(jié)構(gòu)跨越深谷與溝壑。矮塔斜拉橋因同時具有連續(xù)梁橋整體剛度大、經(jīng)濟性好以及斜拉橋跨越能力強等優(yōu)點而成為該地區(qū)常用的橋梁形式[1]。但因缺乏相關(guān)抗震性能研究成果，國內(nèi)外抗震設(shè)計規(guī)范并未提出此類橋梁的簡化設(shè)計方法，而一般采用時程分析法得到地震響應(yīng)。此外，橋梁因地形原因而采用較大跨徑時，地震動的行波效應(yīng)則不應(yīng)忽視。李小珍等[2]發(fā)現(xiàn)相比于一致激勵，矮塔斜拉橋墩柱在非一致激勵下的彈塑性響應(yīng)會增大，因此不考慮行波效應(yīng)易造成墩柱延性設(shè)計的誤判。但項海帆[3]利用影響矩陣概念發(fā)現(xiàn)對于大跨度斜拉橋，非同步激勵能起到抵消位移的有利作用。可見行波效應(yīng)對大跨度橋梁地震響應(yīng)的影響存在兩面性，常因地震動視波速或結(jié)構(gòu)形式等條件而改變[4－5]。此觀點已通過振動臺試驗得到證實[6－7]。因此，在對大跨度矮塔斜拉橋進行地震分析時需采用非一致激勵以捕捉行波效應(yīng)帶來的雙面影響。但非一致激勵的引入極易引起橋梁上部結(jié)構(gòu)發(fā)生碰撞破壞。這一碰撞現(xiàn)象已引起許多學(xué)者的關(guān)注[8－11]，Zheng等[9]以考慮主梁與橋臺間碰撞的連續(xù)橋梁為對象，對比了一致激勵和非一致激勵輸入時的動力響應(yīng)，發(fā)現(xiàn)非一致激勵會增大碰撞帶來的不利影響。但Won等[10]通過時程分析卻得出碰撞的出現(xiàn)能減小墩柱內(nèi)力和位移的結(jié)論。此外，閆聚考等[11]在振動臺試驗中發(fā)現(xiàn)考慮行波效應(yīng)時，大跨度懸索橋與引橋間的碰撞力大小和發(fā)生次數(shù)因地震動不同而存在差異。由此可見地震下的碰撞對橋梁結(jié)構(gòu)響應(yīng)的影響未取得統(tǒng)一定論，其同樣與結(jié)構(gòu)形式和地震動特性有關(guān)。因此，為更為準確地模擬大跨度橋梁在地震作用下的碰撞響應(yīng)，為抗震設(shè)計提供數(shù)據(jù)支持，較為合理的方法是使用多條地震動進行非一致激勵輸入時程分析。但此作法需要消耗大量時間和運算成本，效率較低。

為高效獲取復(fù)雜結(jié)構(gòu)在不同地震動強度下的動力響應(yīng)，伊朗學(xué)者Estekanchi提出了耐震時程法(ETM)的理念[12]，且被證實可用于多種結(jié)構(gòu)體系的抗震分析，如鋼筋混凝土框架[13－14]、鋼框架[15－16]、鋼儲液罐[17]和拱形大壩等[18]。此方法通過輸入幅值隨時間增大的地震動進行結(jié)構(gòu)抗震設(shè)計和性能評估，綜合了時程分析的動力效應(yīng)和Pushover分析的簡便性。此外，對于樁土相互作用或碰撞接觸等復(fù)雜的邊界約束條件，耐震時程法也可捕捉到其對結(jié)構(gòu)響應(yīng)的影響[19－20]。然而這種方法還未被用于考慮行波效應(yīng)時的大跨度矮塔斜拉橋抗震分析中。

本文首先依據(jù)《城市橋梁抗震設(shè)計規(guī)范》中的反應(yīng)譜合成了三條適用于我國橋梁結(jié)構(gòu)的耐震時程曲線；并以一座跨越山谷地帶的典型大跨度矮塔斜拉橋為研究對象，對比耐震時程分析(ETA)與增量動力分析(IDA)結(jié)果，驗證了考慮行波效應(yīng)時，耐震時程分析快速得到大跨度橋梁碰撞響應(yīng)的可行性；最后，采用此方法進行了不同地震動視波速下，矮塔斜拉橋與橋臺間碰撞力、主梁和塔頂位移以及墩柱曲率變化趨勢的分析。

1 耐震時程法

1.1 耐震時程法基本原理

作為一種新的動力評估方法，耐震時程分析的基本理念是將幅值隨時間不斷增長的人工地震動作用于結(jié)構(gòu)上進行動力分析評估。與傳統(tǒng)IDA分析需要對地震動調(diào)幅進行大量運算不同，耐震時程法所施加地震動的幅值是隨時間不斷增大的，因此只需一次時程分析便可使結(jié)構(gòu)完成從彈性到屈服、損傷以至倒塌的全過程。在ETA分析中，耐震時間成為表征地震動強度的指標，因此結(jié)構(gòu)達到目標性能時所經(jīng)歷的耐震時間越長，表明此結(jié)構(gòu)抗震性能越優(yōu)。

得到合適的耐震加速度時程曲線是保證耐震分析準確的關(guān)鍵，在第二代耐震時程曲線的合成中，需滿足從0開始至任意時刻t的地震時程曲線，其所得加速度反應(yīng)譜值與該持時t成線性關(guān)系，即如式(1)所示[21]：

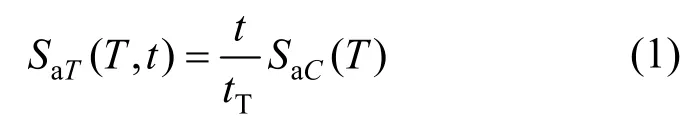
式中：T為結(jié)構(gòu)的自振周期；SaC(T)為規(guī)范反應(yīng)譜；t為任意耐震時刻；tT為用于縮放耐震時程的目標時間；SaT(T,t)為t時刻的目標加速度反應(yīng)譜。

從式(1)可以看出：在tT和SaC(T)給定的前提下，當(dāng)t取為tT/2時得到的反應(yīng)譜為規(guī)范反應(yīng)譜的一半，而取t=tT時的加速度反應(yīng)譜與規(guī)范反應(yīng)譜吻合，以此類推。為滿足式(1)中任意時刻時間t都與反應(yīng)譜保持線性關(guān)系，采用無約束變量優(yōu)化法進行優(yōu)化，得到式(2)：

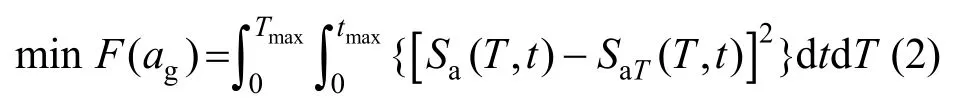
式中：ag為合成的耐震加速度時程曲線；F(ag)為目標耐震方程；Sa(T,t)為0～t時段內(nèi)的耐震加速度反應(yīng)譜；Tmax和tmax分別為優(yōu)化時的反應(yīng)譜最大周期和耐震加速度最大持時。此優(yōu)化方程通過不斷迭代得到一條最優(yōu)地震動ag，使該地震動在任意時刻的反應(yīng)譜和目標譜能最大程度吻合。

1.2 基于我國橋梁抗震規(guī)范的耐震曲線

本文以我國《城市橋梁抗震設(shè)計規(guī)范》(CJJ 166 －2011)的加速度反應(yīng)譜為目標譜，采用MATLAB軟件合成了三條適用于橋梁抗震分析的耐震時程曲線，其中規(guī)范譜的平臺段譜值取為0.5g，對應(yīng)的場地類別、分區(qū)和特征周期分別為Ⅰ類、3區(qū)和0.35 s。在求解式(2)的非線性最小二乘問題時需大量的運算迭代，周期Tmax和耐震持時tmax分別取為6 s和30 s，優(yōu)化間隔分別取為0.01 s和0.05 s，因此，周期和耐震持時優(yōu)化點均為600個；目標時間tT的取值與結(jié)構(gòu)自振周期和耐震曲線最大持時有關(guān)，在本研究中取為10 s，即合成的耐震曲線在0 s～10 s的反應(yīng)譜曲線與規(guī)范反應(yīng)譜曲線保持一致。此外，因優(yōu)化效率與初始輸入地震動有關(guān)，為平衡優(yōu)化時間與精度，以三條SIMQK軟件生成的人工地震動為初始輸入進行優(yōu)化迭代。SIMQK軟件是一種依據(jù)目標反應(yīng)譜合成人工地震動的程序，其機理是從目標譜中計算出功率譜密度函數(shù)，并采用此密度函數(shù)推導(dǎo)出0～2π相位角的不同幅值正弦波，進行組合得到地震時程[22]。使用者可依據(jù)需求合成不同總持續(xù)時間、加速度平穩(wěn)段開始時間和平穩(wěn)段持續(xù)時間等參數(shù)的地震動。本文初始輸入生成準則為：地震動只存在上升段，且同樣以《城市橋梁抗震設(shè)計規(guī)范》中反應(yīng)譜為目標譜。

圖1給出其中一條耐震時程曲線圖以及此耐震曲線在0 s～10 s、0 s ～20 s和0 s ～30 s三個時間段的耐震反應(yīng)譜，并與三個時間段內(nèi)的規(guī)范反應(yīng)譜(將目標規(guī)范譜譜值分別擴大1倍、2倍和3倍)進行對比。從圖1(a)中可以看到耐震時程曲線的峰值隨著時間不斷增長，在三個時間段內(nèi)的最大值分別為0.25g、0.54g和0.72g，與耐震時程法的理念一致。此外，如圖1(b)所示，合成的耐震時程曲線在三個時間段內(nèi)的加速度反應(yīng)譜與規(guī)范反應(yīng)譜均能較好的吻合，表明此條耐震時程曲線滿足合成準則。由式(2)可知合成耐震時程曲線是以加速度反應(yīng)譜為基礎(chǔ)，因此上述與規(guī)范加速度譜的吻合是基本條件。而本文需采用大剛度法對基礎(chǔ)進行位移輸入以考慮行波效應(yīng)[23]，因此需進一步觀察位移譜的吻合性。圖1(c)給出了耐震位移反應(yīng)譜在三個時間段內(nèi)與規(guī)范位移譜的對比。其中規(guī)范位移譜可通過式(3)得到：

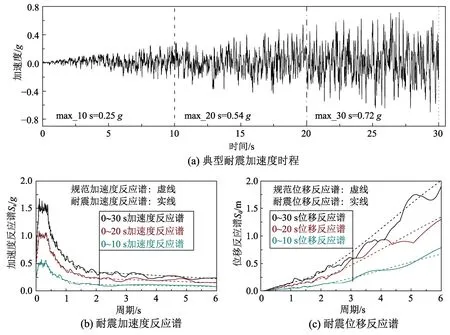
圖1 一條耐震時程曲線及其不同耐震時間下反應(yīng)譜Fig.1 An ET accelerogram and the corresponding response spectra with different endurance time

式中，Sa(T,)ξ和Sd(T,)ξ分別為規(guī)范加速度和位移反應(yīng)譜。圖1(c)中可以看出雖加速度譜保持一致是合成耐震時程曲線的基本條件，但耐震位移譜與規(guī)范位移譜在不同時間段內(nèi)也能很好的吻合，為行波效應(yīng)耐震分析提供可能。

2 橋梁計算模型

2.1 橋梁原型概況

本文以我國山谷地帶某一實際大跨度三塔雙索面矮塔斜拉橋為原型，如圖2所示，跨徑布置為120 m+2×235 m+120 m，左、右側(cè)通過球形鋼支座支撐于橋臺處，伸縮縫寬0.5 m。主梁為寬10.3 m的單箱單室混凝土變截面，如截面A-A所示，梁高由跨中6.5 m按圓曲線變化至支點根部12.5 m，頂板和底板厚則分別由0.6 m和0.5 m變化至1.0 m和1.7 m。主梁上部索塔為雙柱式，中塔和邊塔橋面以上塔高分別為45.0 m和35.5 m，塔身采用矩形實體截面(截面B-B和C-C)，具體尺寸詳見圖2中表格。上部拉索為平行雙索面體系，單側(cè)布置8+9+8=25對斜拉索，拉索在梁上和塔上間距分別為9.0 m和1.1 m，全橋共計100根斜拉索。因山谷地勢高差，從左至右墩柱高度分別為80.5 m、164.5 m和53.5 m，其中左、右墩為混凝土矩形雙肢薄壁式墩柱(截面D-D)，縱橫向長度分別為12.0 m和11.5 m，雙肢中心距詳見圖2中表格；中墩柱采用混凝土空心矩形變截面(截面E-E)，縱向長度為16.0 m，橫向?qū)挾扔?1.5 m漸變至30.0 m。基礎(chǔ)均采用承臺樁基礎(chǔ)，左、右承臺截面為17.4 m×26.6 m矩形，由24根直徑2.2 m鉆孔灌注樁支撐于地基上，其中左側(cè)承臺樁長29.0 m，右側(cè)承臺樁長20.0 m；中承臺截面是31.5 m×37.5 m的矩形，由30根直徑2.8 m鉆孔灌注樁支撐，樁長為25.0 m。

2.2 橋梁有限元模型

基于Sap2000分析軟件建立了考慮主梁與橋臺碰撞和樁-土相互作用影響的三維非線性有限元模型，如圖3所示，其中橋梁縱向為x軸方向。主梁在地震時假設(shè)仍保持為彈性[20]，因此采用彈性模量3.55×104MPa的三維彈性梁單元進行模擬，除承受自重外，主梁上還需考慮橫隔板質(zhì)量和二期恒載。依據(jù)文獻[24]的多塔矮塔斜拉橋振動臺試驗結(jié)果可發(fā)現(xiàn)，主梁上部塔柱在地震下并未出現(xiàn)裂紋和破壞，因此同樣采用彈性梁單元模擬，彈性模量取為3.60×104MPa。考慮到墩柱在地震作用下易遭受損傷，因此對有限元模型的墩柱采用集中塑性單元用于考慮非線性的影響[25－26]；圖3左下部給出塑性區(qū)域的典型彎矩-轉(zhuǎn)角示意圖，其中屈服點和極限點性能指標依據(jù)各截面尺寸和配筋而定，超過極限發(fā)生破壞后，截面承載能力降至極限能力的20%[25]。斜拉索采用桁架單元模擬，彈性模量為1.95×105MPa，同時采用Ernst[27]提出的彈性模型修正公式考慮拉索的垂度效應(yīng)。此外，通過在單元中以P-Δ力的形式施加恒載軸力用于考慮橋塔、墩柱和斜拉索的幾何非線性。為真實模擬出原橋結(jié)構(gòu)的邊界條件，如圖3中下部所示，采用承臺底施加六個方向的彈簧來模擬土與樁基的相互作用，彈簧的平動和轉(zhuǎn)動剛度依據(jù)土層狀況和樁的布置形式按靜力等效原則確定。因重力式橋臺埋置于堅硬巖層中，所以采用與場地固結(jié)約束模擬。橋臺與主梁間的球形鋼支座縱橫向均采用雙線性理想彈塑性彈簧單元模擬，其中初始滑動位移dy取2 mm；為確保支座在地震下不出現(xiàn)脫空現(xiàn)象，豎向剛度取值為無窮大。當(dāng)主梁和橋臺間伸縮縫間隙無法滿足主梁位移響應(yīng)時會發(fā)生碰撞，本研究采用考慮碰撞過程中能量損失的Kelvin碰撞單元模擬此現(xiàn)象[28]，其示意圖見圖3右上部分，碰撞過程中的碰撞力Fp可由式(4)表示：

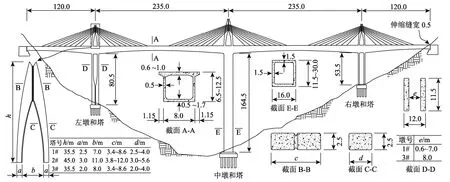
圖2 大跨度矮塔斜拉橋示意圖 /mFig.2 Schematic diagram of the long-span extradosed cable-stayed bridge

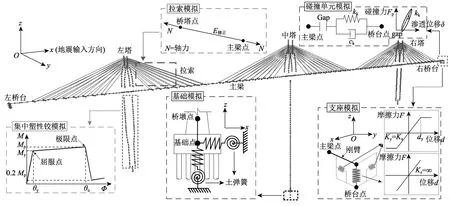
圖3 橋梁三維有限元模型圖Fig.3 The 3D finite element model of the bridge structure

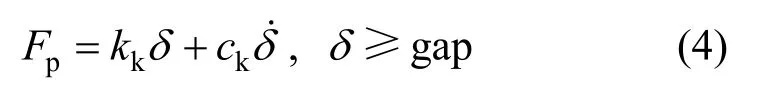
式中：kk和ck分別為接觸剛度和阻尼系數(shù)，具體取值參見文獻[29]；δ和分別為碰撞滲透位移和速度；gap為伸縮縫間隙，本文取0.5 m。

對建立的三維有限元模型進行模態(tài)分析，得到橋梁前兩階周期分別為縱向振動(4.56 s)和橫向振動(3.27 s)。由于本研究僅考慮結(jié)構(gòu)縱向碰撞響應(yīng)，因此地震輸入沿縱向施加。

3 耐震時程法結(jié)果與討論

3.1 耐震時程曲線輸入下的響應(yīng)分析

圖4是三條耐震時程曲線輸入下中塔頂位移和中墩頂彎矩時程圖，從圖4可以看出隨著耐震時間的增長，中塔頂位移和中墩頂彎矩的最大值是在不斷增大的，這與耐震時程法的理念相同。為更好地表征耐震時程的響應(yīng)隨時間不斷增大的特征，同時能與IDA均值結(jié)果保持統(tǒng)一，采用最大絕對值曲線的形式給出耐震時程法結(jié)果，見圖4中實線。后續(xù)分析中，耐震分析結(jié)果均以最大絕對值曲線的平均值形式給出[20]。

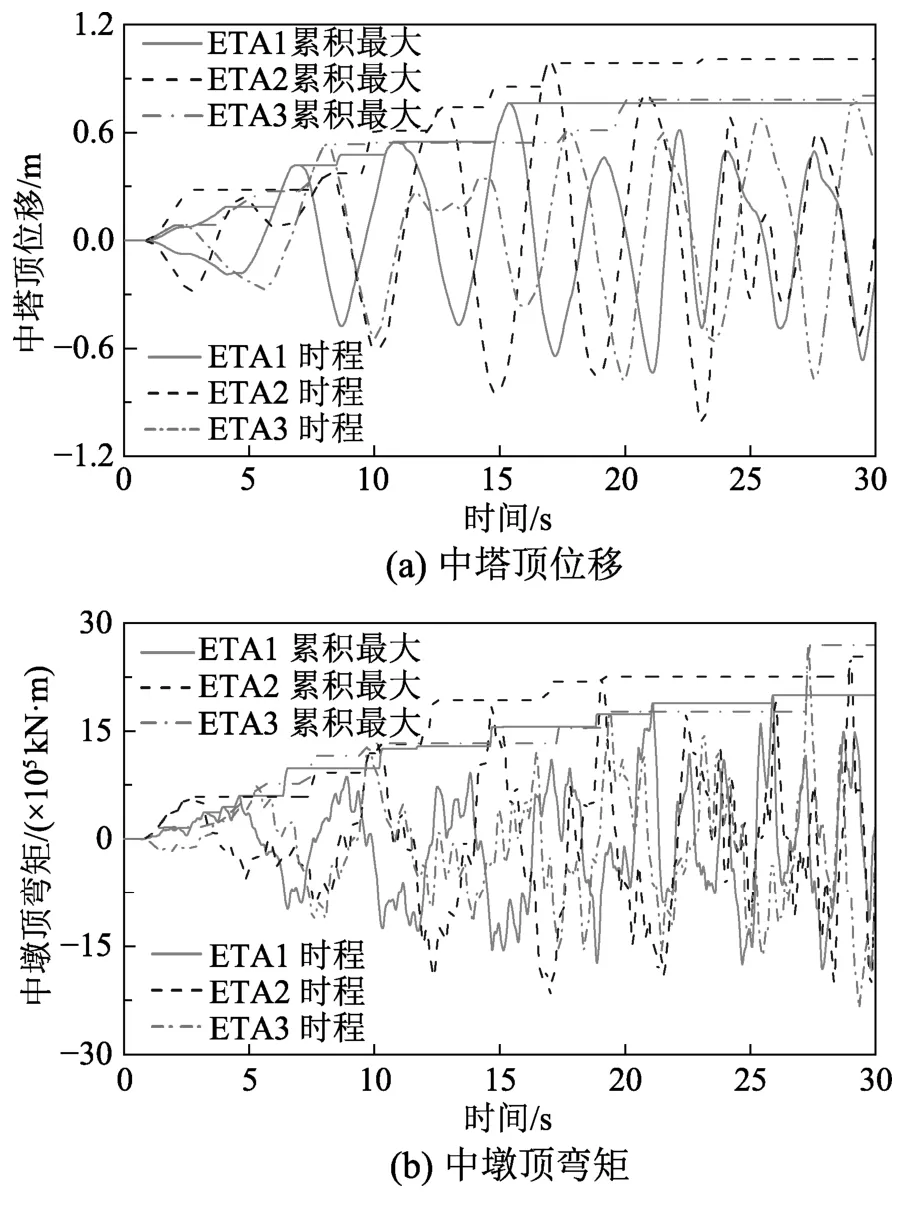
圖4 耐震曲線輸入下中塔頂位移和中墩頂彎矩Fig.4 Top displacement of the middle tower and top bending moment of the middle pier under ET accelerograms

3.2 地震動選取和處理

考慮到IDA分析同樣表征不同地震動強度與結(jié)構(gòu)響應(yīng)的關(guān)系，且理論成熟，得到廣泛運用[30]。因此，本文以該方法結(jié)果為對照組，進行考慮地震動視波速為600 m/s時，耐震時程法能否捕捉到大跨度矮塔斜拉橋碰撞響應(yīng)的研究。

對于IDA方法，首先以合成耐震時程曲線的規(guī)范反應(yīng)譜為目標譜，在PEER-NGA強震數(shù)據(jù)庫中挑選16條天然地震動。挑選原則是調(diào)幅后的16條地震動加速度反應(yīng)譜均值與規(guī)范反應(yīng)譜具有較小的離散性。圖5給出16條調(diào)幅后的地震動加速度反應(yīng)譜均值和規(guī)范譜的對比。從圖5可以看出天然地震動反應(yīng)譜均值和規(guī)范反應(yīng)譜曲線能較好地吻合。對調(diào)幅后的天然加速度時程和合成的三條耐震時程進行兩次積分得到位移時程，并做基線修正處理以消除零位漂移誤差。此外，因碰撞的瞬時性，需將位移輸入的時間間隔線性插值為0.001 s。

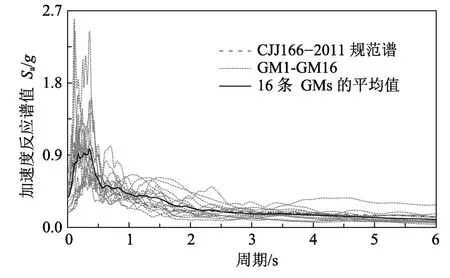
圖5 天然地震動反應(yīng)譜及其均值與規(guī)范反應(yīng)譜對比Fig.5 Response spectra of natural earthquake records and the comparison between their mean spectrum and code spectrum

3.3 適用性結(jié)果分析

考慮到等步長調(diào)幅方法的簡便性且利于軟件程序化[31]，本文IDA分析采用此調(diào)幅方式。通過多次非線性時程分析得到響應(yīng)最大值的離散點，并運用三次Hermite插值獲取完整的IDA曲線。需注意，常用IDA分析表征的是地震響應(yīng)與譜加速度值的關(guān)系，而ETA表征是響應(yīng)與耐震持時的關(guān)系，因此在進行兩種方法對比驗證時需通過式(5)建立起譜加速度值與耐震持時t的關(guān)系：

式中：αm為單條地震動調(diào)幅系數(shù)；SaS(T)為單條地震動反應(yīng)譜值。

圖6給出了視波速600 m/s時，三座索塔在兩種方法下的塔頂位移和塔底彎矩圖，可以看出兩種響應(yīng)的耐震和IDA曲線都隨著時間不斷增大，但與平滑的IDA曲線不同，ETA分析結(jié)果因統(tǒng)計的離散性而呈現(xiàn)鋸齒狀。此外，因行波效應(yīng)的存在，耐震分析下三橋塔第一次出現(xiàn)響應(yīng)值的時間存在差異，如圖6(a)左上角詳圖所示，左、中、右塔頂位移分別在0.200 s、0.592 s和0.983 s后才出現(xiàn)明顯的增長趨勢，但IDA曲線因插值擬合的原因而規(guī)避了此現(xiàn)象。

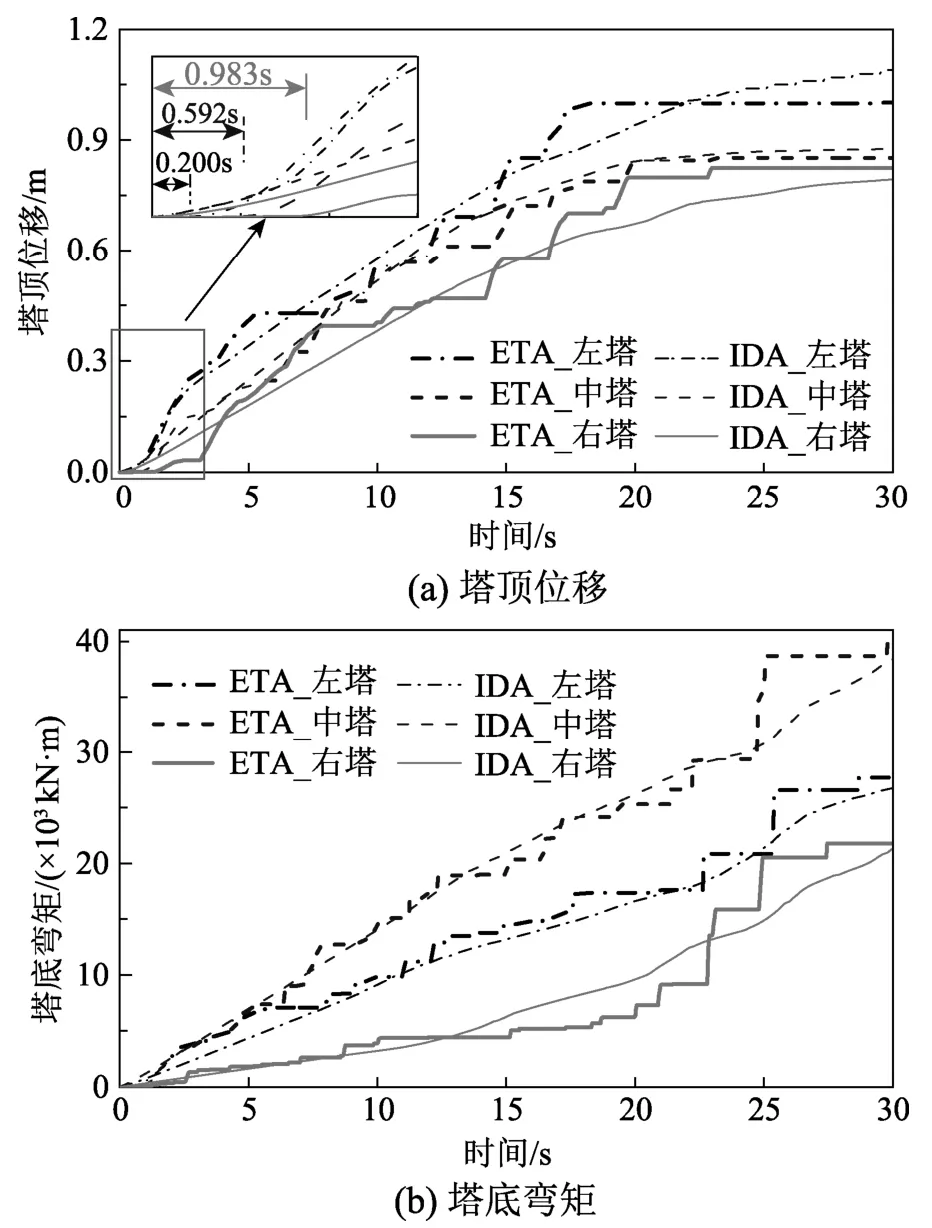
圖6 IDA和ETA方法下橋塔響應(yīng)對比Fig.6 Comparison of responses of the bridge towers between IDA and ETA

對比圖6中的IDA和ETA曲線，發(fā)現(xiàn)不論是塔頂位移還是塔底彎矩，兩者分析結(jié)果均較好地吻合。在圖6(a)中，雖耐震時間20 s附近，兩方法得到的位移值存在一定誤差，左、中、右塔最大誤差值分別為9.32%、2.86%和16.26%，但考慮到ETA只進行了三次分析，相比IDA分析減少95%以上的運算量，且耐震曲線存在“鋸齒”平臺段，因此這些誤差可接受。從圖6(b)可以看出兩方法對于塔底彎矩捕捉與位移類似，即中小震時(小于15 s)彎矩幾乎重合；隨著耐震時間的增長，兩方法的誤差有所增大，但處于可接受范圍內(nèi)。此外，因外型尺寸和索力引起三座橋塔間位移或彎矩的差異，即任何地震動強度下左塔頂位移最大，但彎矩最大卻出現(xiàn)在中塔底的現(xiàn)象，耐震時程法也能很好地捕捉到。表明耐震時程法可有效預(yù)測考慮行波效應(yīng)時上部索塔的位移和內(nèi)力響應(yīng)。

基于軟件分析數(shù)據(jù)結(jié)果，圖7給出了考慮行波效應(yīng)時，主梁中點位移在IDA和ETA兩種方法下的對比結(jié)果，可以看出16條天然地震動IDA均值與三條ETA的均值一致性較好。雖在耐震時間12 s后出現(xiàn)了ETA方法低估主梁位移的現(xiàn)象，最大低估為12.22%，但考慮到大震下碰撞的出現(xiàn)以及支座和橋墩進入非線性等因素使主梁位移響應(yīng)復(fù)雜化，而耐震時程法作為一種預(yù)測主梁碰撞響應(yīng)的快捷方法，此誤差可接受。此外，圖7中同樣可看出ETA曲線因地震動視波速而出現(xiàn)了響應(yīng)滯后現(xiàn)象。

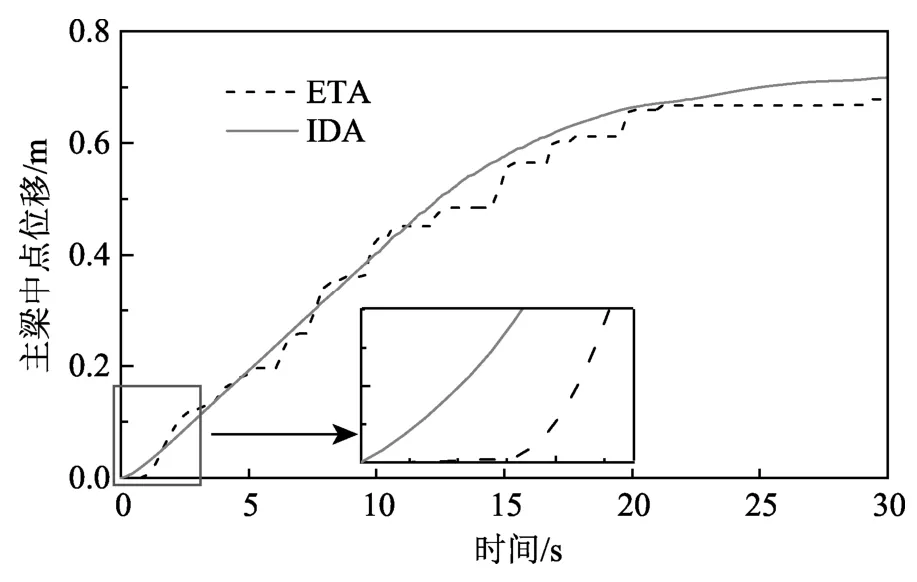
圖7 IDA和ETA方法下主梁位移對比Fig.7 Comparison of displacement of the bridge deck between IDA and ETA

圖8給出左墩頂部和底部彎矩以及對應(yīng)曲率延性系數(shù)的IDA和ETA對比曲線。可以發(fā)現(xiàn)墩底截面在30 s耐震時間內(nèi)一直保持線性；而墩頂部截面在16 s附近進入非線性，此時隨著地震動增大，僅曲率增大而彎矩并未明顯變化。從圖8(a)兩種方法捕捉橋墩彎矩可發(fā)現(xiàn)橋墩頂響應(yīng)曲線基本重合，IDA和ETA幾乎同一時刻捕捉到截面進入塑性，分別是16.192 s和16.765 s；對于墩底彎矩的預(yù)測，ETA雖有高估其響應(yīng)的趨勢，20 s時的誤差達到19.31%，但差距隨著時間增長趨于緩和。此外，對于橋墩頂和墩底截面的延性系數(shù)，耐震時程曲線也能很好地反映出16條天然地震動下的IDA結(jié)果，如圖8(b)所示，最大誤差分別為10.08%和16.86%。從圖8還可以看出，在耐震時間較小時，兩種方法存在明顯誤差，這是因為對于耐震時間較小的情況，兩方法捕捉碰撞力出現(xiàn)的時間存在差異，ETA首次出現(xiàn)碰撞的時間較IDA分析首次出現(xiàn)碰撞的時間提前(見圖9)。

圖8 IDA和ETA方法下左橋墩響應(yīng)對比Fig.8 Comparison of responses of the left bridge pier between IDA and ETA

表1列出了耐震時程法在大震時(大于20 s)預(yù)測左、中、右三墩響應(yīng)與IDA分析的最大誤差。從表1可以發(fā)現(xiàn)中墩頂和墩底在30 s耐震時間內(nèi)均保持為彈性，因此，兩種方法的誤差相比于邊墩更小；此外，表1中兩種方法預(yù)測橋墩響應(yīng)的相對誤差在20%以內(nèi)，但考慮到分析時因引入非線性碰撞單元和行波效應(yīng)，動力響應(yīng)更加復(fù)雜，以及墩身結(jié)構(gòu)在大震下經(jīng)歷強非線性和耐震時程曲線的持時和變化趨勢與真實地震動存在差異(耐震曲線幅值一直增長，而天然地震動具有平臺段和衰減段)，此誤差是可接受的。因此，耐震時程法可用于考慮行波效應(yīng)時大跨度矮塔斜拉橋墩柱碰撞性能評估。

圖9給出了IDA和ETA兩方法下主梁與橋臺間的碰撞力曲線，可以發(fā)現(xiàn)兩方法下碰撞力值以相同的趨勢不斷地隨耐震時間增長，且左側(cè)伸縮縫因較早受地震影響而產(chǎn)生比右側(cè)大的碰撞力。對于左、右側(cè)伸縮縫處碰撞發(fā)生時間，IDA分析結(jié)果得到分別位于9.1 s和11.2 s附近；但ETA分析時，兩側(cè)伸縮縫在5 s前均已發(fā)生碰撞，這是因為行波效應(yīng)使耐震方法下的主梁位移出現(xiàn)滯后現(xiàn)象(圖7)，導(dǎo)致伸縮縫間隙在較小的地震強度下便滿足不了橋臺與主梁間的相對位移，因此碰撞現(xiàn)象更早地發(fā)生。但隨著耐震持時增加到10 s后，ETA分析的碰撞力逐漸與IDA結(jié)果相近。考慮到ETA分析是結(jié)構(gòu)抗震分析的一種簡化方法，此誤差在可接受范圍內(nèi)。因此，耐震時程法可用于預(yù)測大震下大跨度矮塔斜拉橋與兩側(cè)橋臺間的碰撞力大小。

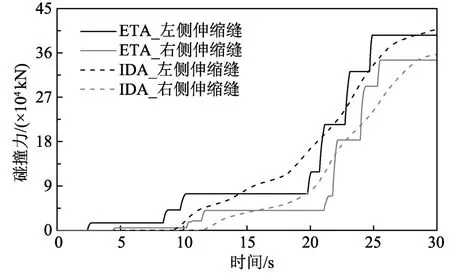
圖9 IDA和ETA方法下碰撞力對比Fig.9 Comparison of the pounding force between IDA and ETA

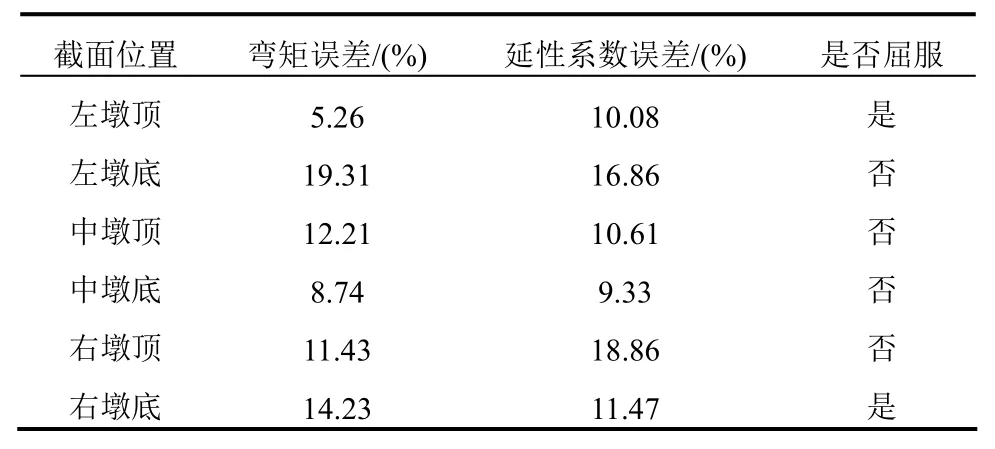
表1 大震時IDA和ETA兩方法橋墩響應(yīng)誤差最大值Table 1 The maximum errors of responses of the piers between IDA and ETA under large earthquakes

4 行波效應(yīng)影響的耐震時程分析

基于3.3節(jié)耐震時程法適用性驗證可知，其是一種僅需少量分析便可解決地震動視波速對大跨度橋梁碰撞影響問題的潛在方法。因此，使用此方法進行不同地震動視波速對大跨度矮塔斜拉橋碰撞響應(yīng)影響的分析。

圖10列出了左、右側(cè)碰撞力在視波速為200 m/s、400 m/s、600 m/s、1000 m/s、1500 m/s和一致激勵下的耐震曲線。由圖10可以看出，當(dāng)視波速為200 m/s或400 m/s時，左、右側(cè)橋臺與主梁發(fā)生第一次碰撞的時間分別約為2.5 s和3.0 s，而一致激勵時，碰撞出現(xiàn)的時間則推遲至10 s后，可見隨著地震動視波速的增大，兩側(cè)伸縮縫第一次出現(xiàn)碰撞力的時間在延后。對于圖10中不同視波速下的碰撞力耐震曲線，可以發(fā)現(xiàn)存在顯著差異性，表明碰撞力大小受地震動視波速的影響。此外，碰撞力值還依賴于地震動強度，如圖10(b)所示，對于右側(cè)伸縮縫處碰撞力，當(dāng)耐震時間處于[10, 22]s時，除視波速為200 m/s外，其他波速下的行波效應(yīng)使碰撞力值有減小趨勢，而其他耐震時間下，視波速有增大碰撞力的效果；同樣的現(xiàn)象也可在圖10(a)的左側(cè)碰撞力曲線中發(fā)現(xiàn)。

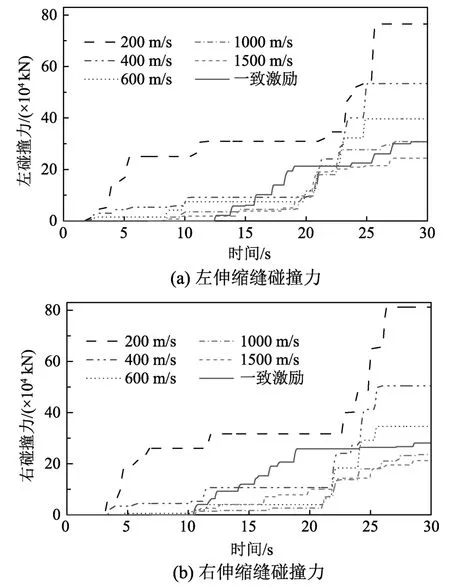
圖10 不同視波速下ETA碰撞力Fig.10 The pounding force with various apparent wave velocities by ETA

圖11給出了不同地震視波速下主梁位移的耐震時程曲線。可以發(fā)現(xiàn)當(dāng)波速大于1000 m/s時，行波效應(yīng)對主梁位移的影響可忽略；而當(dāng)波速小于1000 m/s時，主梁位移明顯小于一致激勵下的響應(yīng)，這是因主梁兩側(cè)的碰撞力對主梁運動起約束作用。但在視波速為200 m/s時的大震下(大于25 s)，因巨大碰撞力且多數(shù)橋墩進入塑性，主梁位移從0.73 m迅速增大到1.11 m。由此可見，即使碰撞單元和行波效應(yīng)等復(fù)雜邊界和輸入條件能減小大跨度矮塔斜拉橋主梁地震響應(yīng)，但因結(jié)構(gòu)自身進入非線性，可能使上述有利作用轉(zhuǎn)變?yōu)椴焕绊憽?/p>

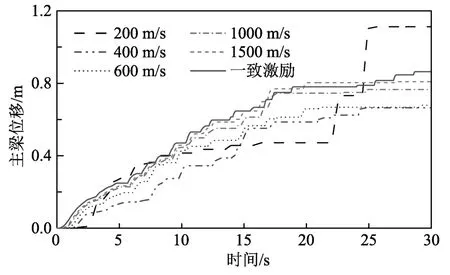
圖11 不同視波速下ETA主梁位移Fig.11 The deck displacement with various apparent wave velocities by ETA

圖12給出了主梁上部三座索塔頂部位移在不同地震動視波速下的ETA分析圖，可以發(fā)現(xiàn)視波速對三座索塔頂位移的影響存在差異。從圖12(a)表達的左塔頂位移耐震圖看出15 s前(200 m/s視波速為5 s前)，行波效應(yīng)對于塔頂位移的影響很小，曲線幾乎重合；但隨著地震動強度的增大，視波速增大左塔頂位移的現(xiàn)象逐漸明顯，且增大幅度與視波速大小無關(guān)，但需注意的是當(dāng)視波速繼續(xù)增大到一定程度時，大震下增大左塔頂位移現(xiàn)象會逐漸減弱，最后與一致激勵下的左塔頂位移保持一致。而視波速對于中塔頂位移的影響與主梁位移相似，如圖12(b)所示，即總體上行波效應(yīng)起抑制位移作用，但大震時的200 m/s視波速下出現(xiàn)位移增大現(xiàn)象。此外，由圖12(c)可知，波速大于200 m/s時的行波效應(yīng)對右塔頂位移影響很小，但波速為200 m/s時需要考慮行波效應(yīng)增大位移響應(yīng)的不利影響。結(jié)合塔頂和上述主梁位移在不同視波速下的ETA分析可知，對于軟土地質(zhì)(視波速一般小于200 m/s)，需考慮地震動行波效應(yīng)帶來的位移增大現(xiàn)象，且右索塔受其影響最大。

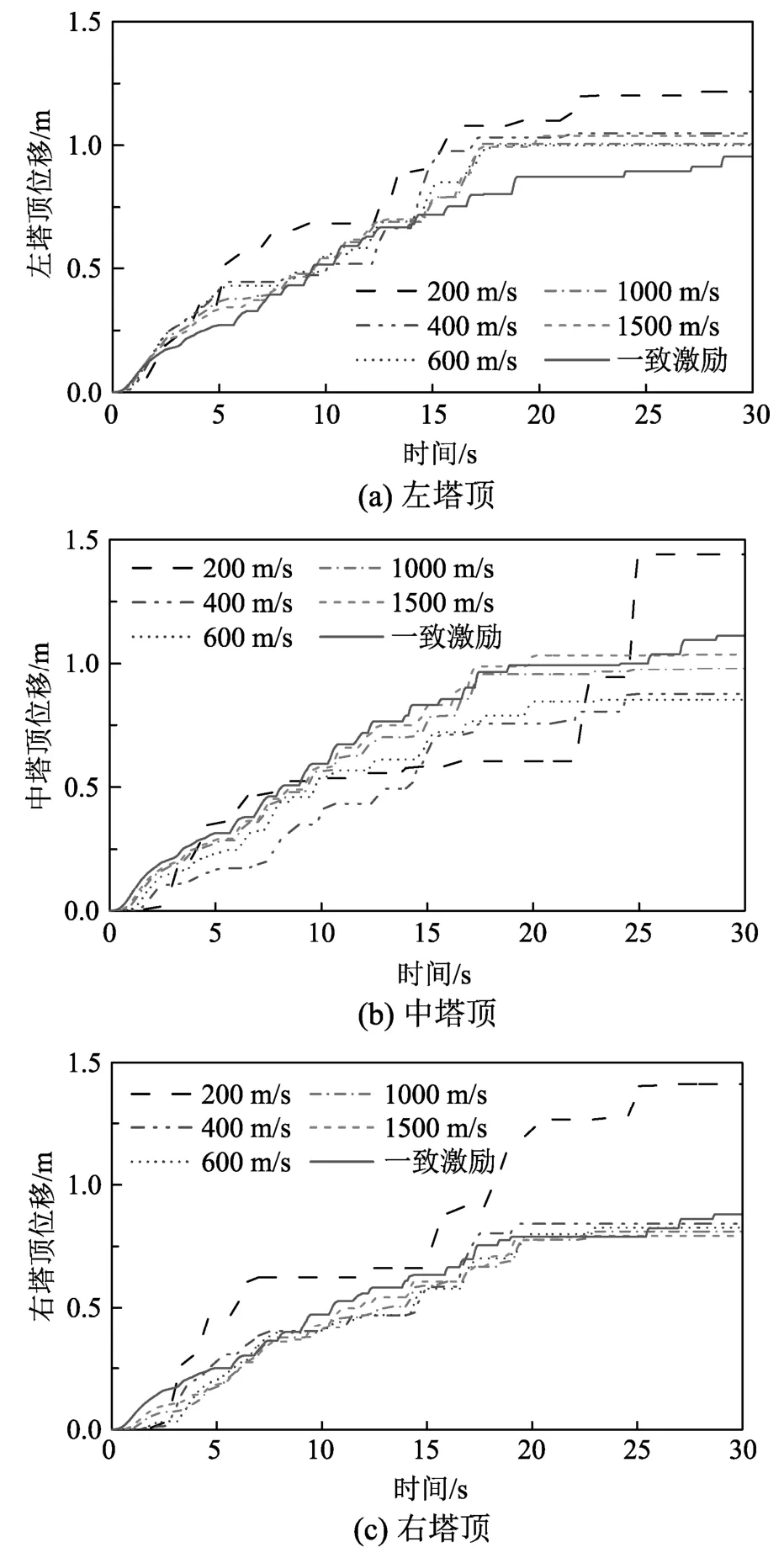
圖12 不同視波速下ETA塔頂位移Fig.12 The displacement of tower top with various apparent wave velocities by ETA

為研究不同視波速對大跨度矮塔斜拉橋墩柱響應(yīng)的影響，圖13給出了橋墩頂部和底部兩處關(guān)鍵截面處的曲率延性系數(shù)耐震圖。由圖13可知，當(dāng)視波速大于200 m/s時，除左墩頂外，其他墩柱關(guān)鍵截面的延性系數(shù)受行波效應(yīng)影響小。與圖13(b)～圖13(f)對比后發(fā)現(xiàn)，對于圖13(a)左墩頂延性系數(shù)，當(dāng)截面屈服后(大于1)，不同波速下的ETA曲線出現(xiàn)離散，表明橋墩截面進入塑性易激發(fā)起不同波速對截面曲率的影響。觀察圖13中波速為200 m/s時的曲線發(fā)現(xiàn)，六個墩柱關(guān)鍵截面的延性系數(shù)明顯大于其他視波速下的對應(yīng)值，可見軟土下左、右側(cè)碰撞力的增大，易加劇墩柱截面進入塑性；此外，當(dāng)墩柱進入塑性后，截面的延性系數(shù)會急劇增大，再一次表明了橋墩截面屈服狀態(tài)與行波效應(yīng)的影響存在相關(guān)性。

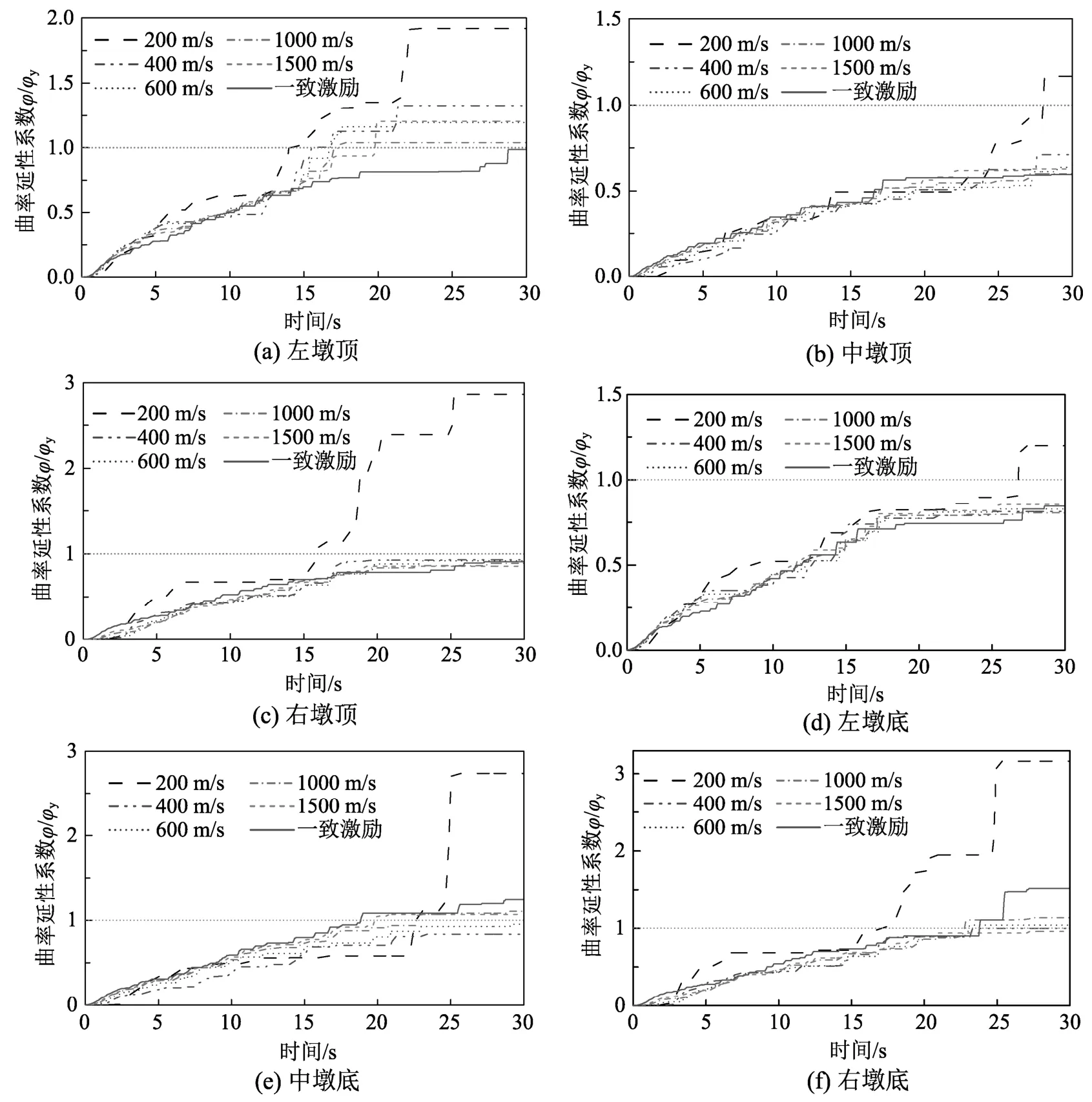
圖13 不同視波速下ETA墩柱關(guān)鍵截面曲率延性系數(shù)Fig.13 The curvature ductility coefficients of the bridge pier with various apparent wave velocities by ETA

5 結(jié)論

基于耐震時程法可高效評估結(jié)構(gòu)地震響應(yīng)的優(yōu)勢，本文以考慮碰撞影響的典型大跨度矮塔斜拉橋為例，驗證了此方法預(yù)測行波效應(yīng)下大跨度橋梁碰撞響應(yīng)的有效性。并在可行性驗證基礎(chǔ)上進行了不同地震動視波速對大跨度橋碰撞響應(yīng)影響的研究。得到主要研究結(jié)論如下：

(1) 考慮行波效應(yīng)時，耐震時程法預(yù)測大跨度橋梁碰撞響應(yīng)與IDA分析結(jié)果存在一定誤差，這是因為耐震時程曲線在持時和變化趨勢與真實地震動存在差異，但ETA作為一種簡化的抗震分析方法，此誤差在可接受范圍內(nèi)。

(2) 耐震時程分析只需少量運算便可表達出多種視波速與地震動強度組合的矮塔斜拉橋碰撞響應(yīng)。

(3) 行波效應(yīng)對大跨度矮塔斜拉橋碰撞響應(yīng)的影響存在復(fù)雜性和不確定性，與地震動視波速、地震動強度和結(jié)構(gòu)是否進入非線性相關(guān)。總體而言，位于軟土地質(zhì)條件(視波速小)的強非線性結(jié)構(gòu)，在大震時應(yīng)考慮行波效應(yīng)的不利影響。

(4) 耐震時程法可用于預(yù)測考慮行波效應(yīng)時大跨度矮塔斜拉橋的碰撞響應(yīng)。但橋梁地震碰撞響應(yīng)易受到各種復(fù)雜條件的影響，如伸縮縫寬度、橋臺動力特性以及局部場地效應(yīng)等[32]。因此，此方法在考慮這些影響因素下的適用性還需進一步研究。