高中數學中的兩個“能量守恒”現象
孟辛亥
(甘肅省華亭市第一中學 甘肅華亭 744100)
大家都知道,化學中有一個重要的定律——“能量守恒定律”。其實,數學中同樣有兩個“守恒現象”值得總結掌握和熟練應用。
一、數列中的“守恒”
在數列問題中,運用“裂項相消法”和“錯位相減法”[1]求和時會遇到此類現象。下文舉例說明。
(2)設bn=,Tn是數列{bn}的前n項和,求使得Tn<m/20對所有n∈N*都成立的最小正整數m。
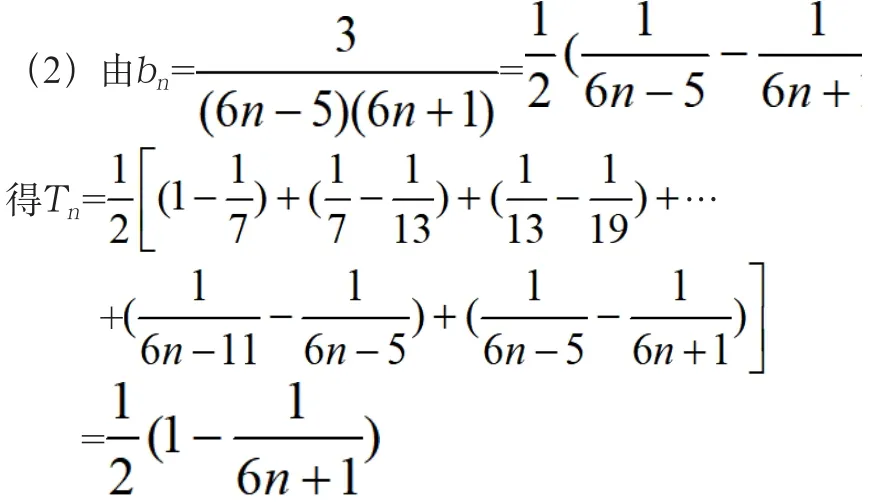
然后易得m≥10。
總結:由于分母是一個等差數列的相鄰兩項之積,故在裂項相消的過程中會發現剩余的兩項是一正一負,即一首一尾。這正好體現了一種守恒。掌握這一現象后,學生自然會在計算過程格外注意剩下的項,不會發生少項或多項的錯誤。
(同學們在做完之后會發現什么規律呢?提示:分母是相間項之積,故相消后剩余的項是兩正兩負,即兩正首兩負尾。)
此外,在用“錯位相消法”求和時,列式相減環節也會有一個守恒現象,即第一次是-0,最后一次(第n+1次)是0-q,也是首尾一正一負。
二、三角函數中的“守恒”
二倍角公式和半角公式極好地體現了“角系數和次數”[2]一升一降的守恒。
二倍角公式,如cos2α=2cos2α-1=1-2sin2α可以稱為次升系降。而由半角公式也可得sin2α=,我們不妨稱降次公式更為恰當,即次降系升。半角畢竟特殊的,而應用的時候,角是相對靈活的。
如此就能很好地防止類似錯誤,如:

防止此類錯誤的一個辦法就是通俗地理解角系數降實為縮小1/2,角系數升實為擴大2倍,則上兩式學生不難得出正確結果:

例2 已知函數f(x)=sin2x+sinxcosx+2cos2x,x∈R。
(1)求函數f(x)的最小正周期和單調增區間;
(2)函數f(x)的圖象可以由函數y=sin2x(x∈R)的圖象經過怎樣的變換得到?
分析:此題關鍵是對f(x)的化簡,運用什么公式呢?
不合理的化簡:
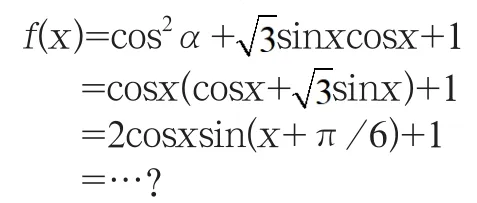
如此,雖然老師可以運用積化和差公式最終得出結論,但一來費時費力,二來新教材降低了難度,不要求運用積化和差公式。對學生而言,他們就只能鉆進死胡同。
合理的化簡:運用降次公式,可保初次化簡后得到同角(2α)一次的有利效果。有

以下求解容易多了,這里不再說明。
在這里,學生處理時常常感到公式記住了,但難以正確、靈活地應用。如果能在這里掌握這一現象并學會處理三角問題時“先角后名”的方法,學生就會輕松自如得多。
應用練習:已知α為銳角,且tanα=1/2,求的值。

