例談一線三等角模型的建立與應用

鄒藝宣

(福建省漳州市華安一中 363800)

一、模型呈現

如圖1，點A、E、C在同一條直線上，已知∠1=∠2=∠3=α，其中α角可以是任意的角，可以是銳角、直角或鈍角，都有結論：△ABE≌△CED.

證明因為∠1=∠2=∠3=α，所以∠B+∠AEB=180°-α，∠DEC+∠AEB=180°-α,所以∠DEC=∠B，又∠1=∠3，所以△ABE≌△CED.

這個基本模型的特征是有三個相等的角，且三個角的頂點在同一條直線上，則它們的邊所構成的兩個三角形會始終相似.我們把這個基本圖形稱為一線三等角模型.

二、模型應用

1.顯性模型，直接應用

例1如圖2，在△ABC中，AB=AC=5,BC=8,點P是BC上的一個動點(不與點B、C重合)，連結AP，作∠APQ=∠B，PQ交AC于點Q.

(1)若BP=2,求CQ的長；

(2)若BP=x,CQ=y,求y關于x的函數關系式，并求出當BP為何值時CQ取得最大值.

分析第(1)問題目所給條件很明顯已經具備一線三等角模型的特征，所以熟悉這個模型就可以快速聯想到可以用相似來解題，可以提高解題的速度.第(2)問是要求由動點產生的最值問題，這是初中生的一個難點，但是第(2)的解答可以從第(1)題獲得啟發，兩題之間是有聯系的，只是把數字換成了字母，所用的方法是一樣的，還是由一線三等角模型可以得到三角形相似，利用對應邊成比例就可以得到y和x的函數關系式，再利用函數知識即可求出最大值.

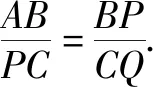
例2如圖3，矩形ABCD中，AB=8,AD=10.點E是AB邊上一點，把△ADE沿直線DE翻折，使點A恰好落在BC邊上的點F處，則DE=.

2.隱性模型，構造轉化

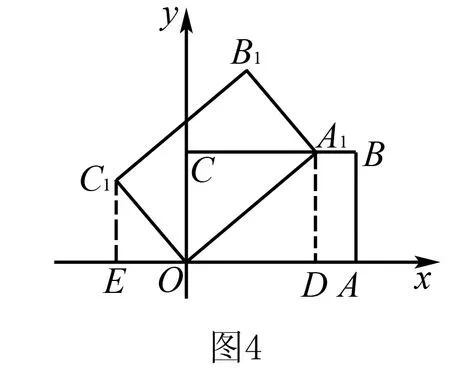
例3如圖4，矩形OABC的兩邊OA,OC分別在x軸和y軸上，并且OA=5，OC=3若把矩形OABC繞著O點逆時針旋轉，使點A恰好落在BC邊上的A1處，則點C的對應點C1的坐標為( )

分析本題乍一看條件沒有滿足一線三等角模型的特征，但要求點的坐標，常添加的輔助線是過所求點C1作坐標軸的垂線，所以過點C1作C1E⊥x于點E，則會發現∠C1EO=∠C1OA1=90°.聯想到一線三垂直模型，只要再過點A1作A1D⊥x于點D，則很快就可以找到解題的突破口.由△C1EO∽△ODA1得出答案為A.

分析本題乍看不符合一線三等角模型，但時如果注意到∠DFE=∠OAB=90°,已經有點模型的影子，只要過點D作DH⊥OA于點H，則馬上構造出一線三等角模型，快速找到解題的突破口.

在解決數學問題時，“如何找到解題的突破口”是很多學生較為困惑的.很多學生解題時沒有思路和方向，而基本模型的提煉學習，可以幫助學生在眾多的數學問題中找到具有共性的模型，這樣可以為學生解題提供準確的解題思路和線索，還可以提高學生的數學核心素養.