基于刃邊法的紅外圖像目標信息復(fù)原

孟 浩,李 博,楊耀森

(中北大學(xué)儀器科學(xué)與動態(tài)測試教育部重點實驗室,山西 太原 030051)

1 引 言

紅外熱成像作為一種溫度檢測技術(shù),可應(yīng)用于航空航天、電子、醫(yī)療、機械等行業(yè)。與常規(guī)的檢測手段相比,具有快速、高效以及非接觸式的優(yōu)點。在檢測過程中,由于紅外成像系統(tǒng)本身的因素以及電子噪聲、熱噪聲等,會造成紅外圖像出現(xiàn)模糊、失真,使得圖像效果變差,導(dǎo)致無法精確測量溫度細節(jié)[1]。通常,要提升紅外圖像的測量精度,一種方法是提升紅外熱像儀的各項參數(shù),但在提升參數(shù)的同時也意味著高額的成本[2]；另一種方法是通過圖像復(fù)原方法改善熱像儀的圖像質(zhì)量,在降低成本的同時盡可能獲得物體更多的溫度細節(jié)[3]。

目前,國內(nèi)外研究者對于紅外圖像復(fù)原的研究已經(jīng)做了許多工作,并在一定程度上提高了圖像質(zhì)量。陳樹越等人首先確定熱源圖像的高斯點擴散函數(shù),采用維納濾波的方法復(fù)原紅外圖像中的熱源[4],在提升邊界清晰度的同時更好的保留了熱源信息；李思儉等人將原始圖像經(jīng)過維納濾波后,再做銳化處理,來增強目標邊緣[5],對于運動模糊的圖像復(fù)原效果明顯；賴富文等人利用通過反卷積方法實現(xiàn)對低分辨率紅外熱像儀的增強,比較了正則化卷積與盲卷積對于熱圖像復(fù)原的效果[6],提升了熱圖像的對比度與空間分辨率；周程灝等人采用點插值法,循環(huán)矩陣模型,拉普拉斯正則化方法和共軛梯度迭代法,建立了空間變化圖像復(fù)原方法[7],并通過實驗驗證了復(fù)原方法的有效性。

本文根據(jù)紅外圖像復(fù)原模型[8-11],在利用刃邊法求取紅外熱像儀的點擴散函數(shù)(PSF)時,采用Prewitt銳化算子檢測刃邊,使用三次樣條插值算法以及Savitzky-Golay 濾波對邊緣擴散函數(shù)(ESF)進行優(yōu)化,利用維納復(fù)原與盲卷積復(fù)原算法復(fù)原熱圖像,并對比了兩種方法的復(fù)原效果。

2 紅外圖像復(fù)原模型

基于Stefan-Boltzmann定律,物體發(fā)出的紅外光與其溫度有關(guān)。與傳統(tǒng)的光學(xué)成像系統(tǒng)類似,紅外熱像儀的成像可通過一個線性系統(tǒng)進行表述:

g(x,y)=h(x,y)*f(x,y)+n(x,y)

(1)

其中,g(x,y)指紅外熱像儀觀察的溫度分布；f(x,y)為未知場景圖像真實的溫度分布；n(x,y)為紅外測量系統(tǒng)中的加性噪聲；h(x,y)是定義從f(x,y)到g(x,y)映射的系統(tǒng)矩陣。

光學(xué)系統(tǒng)在近軸成像區(qū)可視為線性不變系統(tǒng),假設(shè)系統(tǒng)的輸入f(x,y)是一線脈沖,假定為一個平行于y軸的線光源δ(x),于是有:

f(x,y)=δ(x)

(2)

系統(tǒng)對于線脈沖的輸出響應(yīng)g(x,y)稱為系統(tǒng)的線擴散函數(shù)(LSF),即:

L(x)=g(x,y)

=δ(x)*h(x,y)

(3)

式中,h(x,y)為系統(tǒng)的脈沖響應(yīng)或點擴散函數(shù)(PSF)。

線擴散函數(shù)L(x)的一維傅里葉變換等于系統(tǒng)的傳遞函數(shù)沿fx軸的截面分布:

(4)

由于脈沖響應(yīng)是旋轉(zhuǎn)對稱的,則傳遞函數(shù)也是旋轉(zhuǎn)對稱的,所以只需要一個截面H(fx,0)就能完全確定系統(tǒng)的傳遞函數(shù)H(fx,fy),調(diào)制傳遞函數(shù)(MTF)是系統(tǒng)傳遞函數(shù)的歸一化模型。

線擴散函數(shù)L(x)為邊緣擴散函數(shù)(ESF)E(x)的導(dǎo)數(shù):

(5)

3 方 法

3.1 復(fù)原參數(shù)計算

準確得到PSF對于圖像復(fù)原的效果至關(guān)重要。根據(jù)輸入信號的不同,PSF的測量可分為點光源法、刃邊法、脈沖法和周期靶標法等,考慮到測量精度與方法實施的經(jīng)濟性,刃邊法能在保證測量精度的同時降低實驗成本[12],且一般的紅外圖像中都會有刃邊。

其求取步驟為:傾斜目標刃邊,使得刃邊與紅外成像器件像素組成的列(行)相交成一定的角度θ；使用Prewitt銳化算子檢測刃邊,以刀刃邊與每行像素的交點作為邊緣分界點；讀取每一行像素的灰度值,并以邊緣分界點為基準對每行灰度值曲線相加求平均得到ESF；將獲得的ESF進行微分得到LSF,LSF的傅里葉變換是空間頻域中的一維系統(tǒng)傳遞函數(shù)STF,對STF進行歸一化后得到MTF；由于成像系統(tǒng)均是旋轉(zhuǎn)對稱的,通過在頻域中旋轉(zhuǎn)一維STF獲得二維STF,再進行傅里葉逆變換即可得到空間域中的PSF。其中,ESF曲線的提取是保證刃邊法計算精度的關(guān)鍵之一。

ESF曲線的提取是根據(jù)校準后刃邊邊緣位置,對圖像進行重新排布,并進行噪聲抑制[13]。本文采用三次樣條插值算法與Savitzky-Golay濾波來優(yōu)化ESF曲線,在消除噪聲的同時進一步平滑ESF曲線。三次樣條插值是通過形成一系列的中間值來使曲線光滑,在已知點與其函數(shù)值相等,導(dǎo)數(shù)與二階導(dǎo)數(shù)在分段的交界點也相等；Savitzky-Golay濾波器是一種基于局域多項式最小二乘法擬合的濾波方法。這種濾波器最大的特點在于在濾除噪聲的同時可以確保信號的形狀、寬度不變,去除高頻信號的同時擬合信號的低頻部分。

3.2 維納濾波復(fù)原

維納濾波器是去除退化后圖像的模糊與噪聲是一種理想的濾波器,其頻域形式為:

(6)

其中,H是退化函數(shù),即PSF;G為退化圖像的傅里葉變換；H*是H的復(fù)共軛;Snn代表噪聲的功率譜;Sf代表未退化圖像的功率譜。

3.3 盲卷積復(fù)原

盲反卷積方法假定光子檢測過程中呈泊松分布,并基于貝葉斯公式得到迭代函數(shù)。其可以在沒有退化圖像先驗知識的情況下進行圖像復(fù)原。

結(jié)合圖像的退化模型,可以得到迭代函數(shù):

(7)

其中,fi是第i輪迭代復(fù)原的圖像;h為退化函數(shù);g為退化圖像。當紅外測量系統(tǒng)的PSF已知,只需要有一個估計值即可進行迭代求解[14],直至收斂。

3.4 復(fù)原效果評估

紅外圖像存在邊緣模糊,因此可以采用邊緣銳度(EAV)算法評估紅外圖像復(fù)原的清晰度。復(fù)原后的紅外圖像越清晰,其邊緣也越清晰,邊緣的灰度變化也越劇烈。該算法銳度計算公式如下:

(8)

式中,表示圖像邊緣銳度,是沿邊緣法向的灰度變化率,是該方向總體灰度變化的絕對值[15]。

此外,還可以采用紅外復(fù)原圖像的標準差來判斷復(fù)原的效果。標準差是指圖像像素灰度值相對于均值的離散程度,如果標準差越大,表明圖像中灰度級分別越分散,圖像質(zhì)量也就越好。

4 實驗結(jié)果與分析

實驗所使用的熱像儀參數(shù)為:分辨率 640×480,光譜范圍7.5～14 μm,熱靈敏度<0.08 ℃,最小焦距0.52 m,測溫范圍-20～2000 ℃,測量精度為±2 ℃或讀數(shù)的2 %。

4.1 PSF的參數(shù)測量

獲取了熱像儀與黑體爐之間鋼板處的熱圖像,如圖1(a)所示;在鋼板與黑體爐交界邊緣產(chǎn)生了刃邊,采用Prewitt銳化算子檢測刃邊,檢測結(jié)果如圖1(b)所示,邊緣檢測算子檢測出分界像素點的位置；以分界像素點為中心,對刀刃區(qū)域所有行進行平均計算ESF,并采用三次樣條插值算法與Savitzky-Golay濾波優(yōu)化ESF,以減輕噪聲影響；如圖1(c)所示,優(yōu)化后的ESF與原曲線近似一致,在細微處相較原曲線更為平滑;對ESF進行微分得到LSF,并使用高斯函數(shù)對LSF進行擬合,如圖1(d)所示。擬合得到的LSF與原曲線近似一致,擬合度(R-square)為95.32 %;對LSF進行傅里葉變換,并進行歸一化處理后得到調(diào)制傳遞函數(shù)MTF,如圖1(e)所示；對LSF進行傅里葉變換,轉(zhuǎn)置叉乘運算后,再進行傅里葉逆變換,得到系統(tǒng)的PSF,如圖1(f)所示。

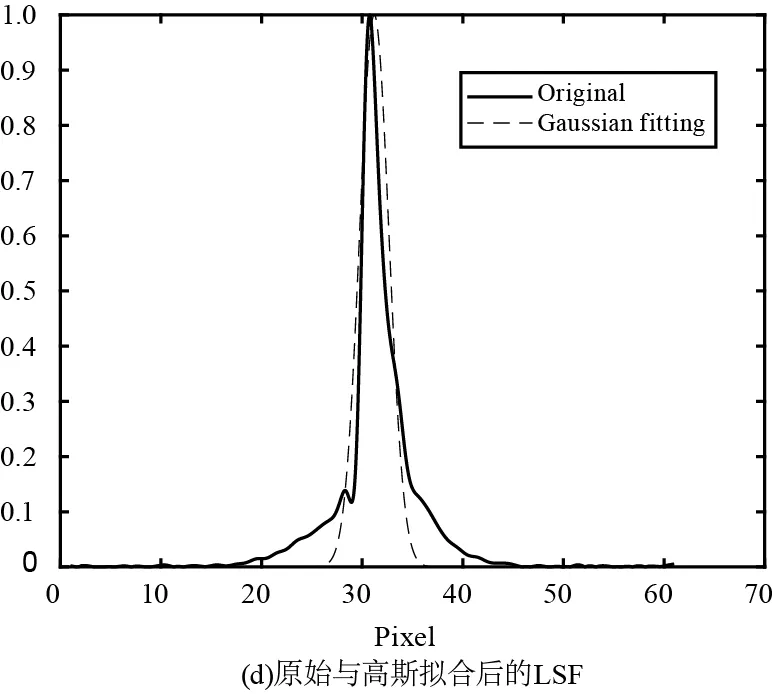
圖1 PSF的復(fù)原參數(shù)

4.2 復(fù)原后的噪聲特性

對于紅外圖像復(fù)原后的熱噪聲特性,研究了兩種復(fù)原方法下的溫度波動,溫度波動越大,對于噪聲的優(yōu)化能力越弱。使用熱像儀對一杯60 ℃左右的熱水進行拍攝,圖2(a)、(b)、(c)分別顯示了原始以及經(jīng)過兩種方法復(fù)原后的圖像。使用圖像中心的正方形區(qū)域(區(qū)域大小為50×50)來計算溫度的最大值、最小值、平均值與標準差,如表1所示。從表1中可以看出,兩種方法均維持了平穩(wěn)的溫度波動,即保持了原始圖像低熱噪聲特性。維納復(fù)原降低了原圖像的標準差,而盲卷積復(fù)原提升了標準差,即維納復(fù)原對于熱噪聲的改善優(yōu)于盲卷積復(fù)原。

圖2 原始與復(fù)原后的熱水圖像

表1 圖像復(fù)原后的溫度波動

Tab.1 Temperature fluctuations after image restoration

MaxMinMeanStdOriginal62.9561.1562.120.3329Wiener62.9261.2262.150.2997Blind62.9561.1762.130.4182

4.3 復(fù)原后的邊界

對于復(fù)原后的熱源邊界,在帶有矩形孔洞的鋼板下設(shè)置熱源進行實驗。圖3(a)、(b)、(c)分別顯示了原始與兩種方法復(fù)原后的圖像。提取三幅圖像中心同一行的一維溫度曲線,如圖4所示。可以看到兩種方法均提升了條紋邊緣高溫與低溫的對比度,對邊界的區(qū)分更加明顯,圖像更為清晰,且維納復(fù)原相比于盲卷積復(fù)原在圖像的高溫和低溫區(qū)域有更好的溫度均勻性。表2給出了采用邊緣銳度算法以及標準差對于圖像復(fù)原效果的定量評估,結(jié)果表明,兩種方法均提升了圖像的邊緣銳度與標準差,增強了紅外圖像的清晰度,且維納復(fù)原相比于盲卷積復(fù)原的提升效果更加明顯。

表2 圖像復(fù)原效果比較

圖3 原始與兩種方法復(fù)原后的條紋圖像

圖4 原始與復(fù)原圖像的一維溫度曲線

5 結(jié) 論

本文首先分析了紅外圖像降質(zhì)原因,通過圖像退化模型提出基于刃邊法的紅外圖像復(fù)原。采用刃邊法對復(fù)原參數(shù)進行計算,通過三次樣條插值以及Savitzky-Golay 濾波對復(fù)原參數(shù)進行優(yōu)化,得到系統(tǒng)的PSF。分別利用維納復(fù)原和盲卷積復(fù)原對原始圖像進行復(fù)原處理,并對復(fù)原后圖像清晰度進行評估。實驗結(jié)果表明,兩種方法均能夠在低熱噪聲特性下增強圖像的對比度,提升圖像的清晰度；維納復(fù)原相比于盲卷積復(fù)原對圖像邊緣銳度以及標準差的提升效果更好一些,且對于熱噪聲的改善也優(yōu)于盲卷積復(fù)原。