基于碼頭集卡共享的運輸任務分配優化模型

曾慶成 于婷

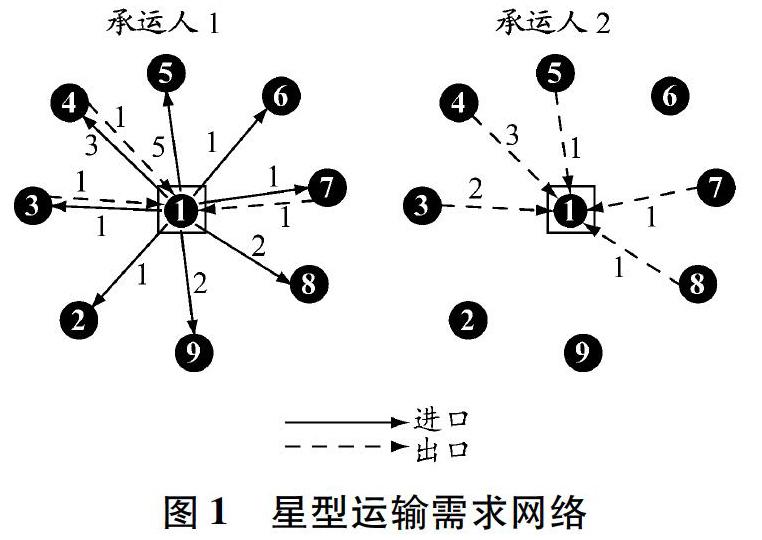
摘要：為提高港口集疏運效率，減少集卡空駛，提出一種基于集卡共享的任務分配方法。以最大化承運人的總利潤為目標，引入補償機制激勵承運人合作，考慮進出口任務的截止時間、承運人車隊大小，建立基于碼頭集卡共享的任務分配模型。通過優化進出口任務分配，減少集卡空駛，并設計啟發式算法求解模型。分析不同情景下承運人的利潤變化，并通過算例分析驗證算法的有效性。結果表明：基于集卡共享的任務分配模型能夠有效地對任務分配過程進行優化和控制，進而提高集卡作業效率。

關鍵詞： 集裝箱碼頭; 集疏運系統; 遺傳算法; 集卡共享; 任務分配

中圖分類號： U169.71 ? ?文獻標志碼： A

Abstract： In order to improve the efficiency of port collecting and distributing system and decrease the unloaded distance of trucks， a task allocation method based on truck sharing is proposed. With the objective of maximizing carriers total profit， a compensation mechanism is introduced to motivate carriers to cooperate together. Considering the deadline of import and export tasks and the size of carriers fleet， a task allocation model based on truck sharing is developed. The unloaded distance of trucks is decreased by optimizing the allocation of import and export tasks. A heuristic algorithm is designed to solve the model. The carriers profit change under different conditions is analyzed， and the validity of the algorithm is verified by example analysis. Results indicate that the task allocation model based on truck sharing can effectively control and optimize the process of task allocation， and then improve the operation efficiency of trucks.

Key words： container terminal; collecting and distributing system; genetic algorithm; truck sharing; task allocation

我國港口集裝箱有80%以上通過公路集疏運，由外集卡完成進港-出港的拖運作業。大量的拖運作業導致高峰時段碼頭擁堵，這不僅會嚴重影響集疏運效率，降低碼頭運營效率，而且會加劇港區污染。此外，由于進出口運輸任務不平衡，大量的集卡都是單程運輸，所以集卡運輸成本高，集疏運效率低。

國內外學者針對集卡調度和任務分配問題開展了大量研究。集卡的路徑優化方面：曹慶奎等[1]探討了成本對路徑選擇的影響，并建立了面向作業面的集卡路徑成本優化模型;李廣儒等[2]分析了整個碼頭水平作業的動態調度方案，提出一種求解集卡動態調度路徑的自適應蟻群算法，進而提高集卡利用率;ZHANG等[3]研究了多個倉庫和碼頭的集卡……