淺談培養高中生數形結合思想的意義

許華

數學是一門抽象、嚴密的學科，教師應培養學生良好的思維習慣，通過日常教學盡早地讓學生了解并逐步熟悉各種數學思想方法，讓學生能處于較高的位置去進行思考和分析問題，正確決策合適的解題策略。

數形結合思想是將抽象的代數關系與直觀的幾何圖形聯系起來，巧妙地將數量的精確刻畫與空間形式的直觀形象結合在一起，充分利用這種結合，找到解題思路的一種思想。

本文結合教學實際，談談培養數形結合思想在教學中的意義。

一、培養數形結合思想，提高抽象思維能力

概念是數學知識的基礎，抽象的數學概念教學學生常難于理解。以新授課選修2-2《§1.1.3導數的幾何意義》為例。

（四）引出新課

教師黑板書寫導數的幾何意義，當點P_n無限逼近P點時，即△x→0時，割線PP斜率的極限是曲線在點處的切線的斜率。學生打開課本，畫重點，記筆記。

課堂上每位學生執筆在紙上逐步畫出點P_n趨于點P時，割線PP_n的變化情況，觀察、歸納、抽象概括得出結論。教師再結合信息技術工具，動態演示割線PP_n的變化過程以加深學生對抽象定義的理解，最后自然過渡引出切線的定義及導數的幾何意義。數形結合思想滲透在教學中，學生積極參與，驗證了知識的生成過程，學會用數學眼光觀察和理解問題，培養了抽象思維能力。

二、培養數形結合思想.提升學生創新意識

教師提供學生充足的思維探究空間，讓學生憑借自己學習和生活的經驗去感受，通過自我探索去發現規律、驗證猜想。教師可以引導和培養學生去設計部分教學課程，如《幾何花板畫函數圖像》這節上機課由學生小連完成教學設計并授課。他首先自學了幾何畫板軟件，并反復練習熟練使用。然后根據課程安排設定具體的課堂學習內容，他認真鉆研，查閱資料，積極和我溝通，反復修改教學設計共六次。

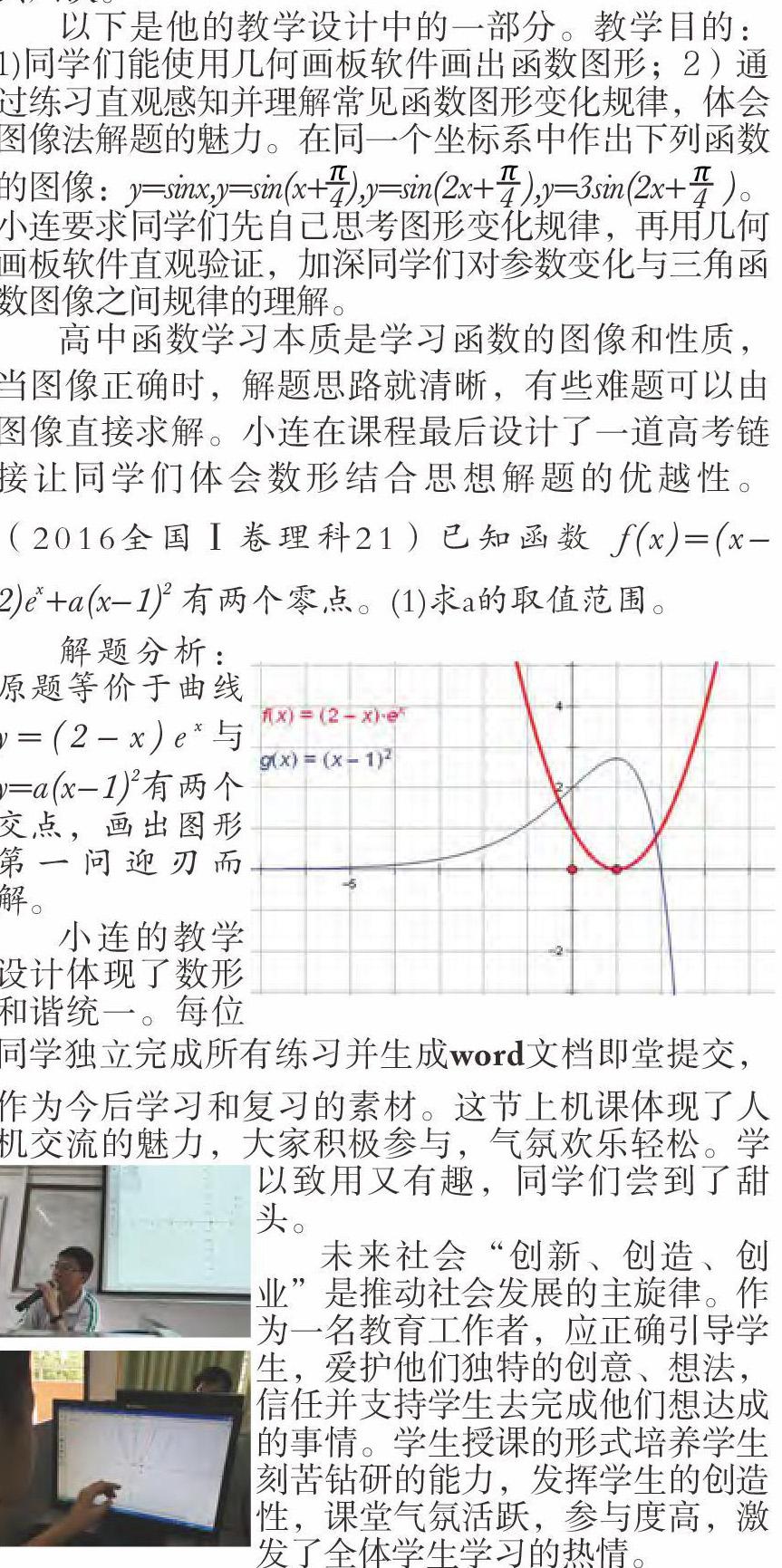
高中函數學習本質是學習函數的圖像和性質，當圖像正確時，解題思路就清晰，有些難題可以由圖像直接求解。小連在課程最后設計了一道高考鏈接讓同學們體會數形結合思想解題的優越性。

小連的教學設計體現了數形和諧統一。每位同學獨立完成所有練習并生成word文檔即堂提交，作為今后學習和復習的素材。這節上機課體現了人機交流的魅力，大家積極參與.氣氛歡樂輕松。學以致用又有趣，同學們嘗到了甜頭。

未來社會“創新、創造、創業”是推動社會發展的主旋律。作為一名教育工作者，應正確引導學生，愛護他們獨特的創意、想法，信任并支持學生去完成他們想達成的事情。學生授課的形式培養學生刻苦鉆研的能力，發揮學生的創造性，課堂氣氛活躍，參與度高，激發了全體學生學習的熱情。

三、數形結合思想與一題多解的結合運用提高學生數學能力

課堂教學遵循數學規律，深入淺出，讓學生更易理解。數形結合思想幫助學生梳理新舊知識的聯系，構筑完善的數學知識框架。一題多解訓練學生數學思想和方法的熟練運用，提升優化學生的思維品質，促進數學學習能力。

解析幾何法通過建立適當的坐標系（如：直角坐標系、極坐標系等），運用坐標將幾何圖形轉化為坐標間的代數關系。解題時先根據題意逐句分析，準確畫圖，再利用圓錐曲線的定義、性質等進行分析求解，體現了文字語言、圖形語言、數學語言間的轉化。下面以選修4-4《坐標系與參數方程》P₂₈例題1為例。

點M到直線x+2y-10=-0的距離取最小值。

課堂上運用一題多解的教學方式，通過同學們的分享，集思廣益，拓展思維的深度和廣度。這些不同的解法蘊含了多種數學思想，而數形結合思想使得抽象問題形象化，輔助學生更清晰地去理解題意。尤其在高三復習課，許多綜合性題目往往解法多種，引導學生結合圖形理解問題，對比分析各種解法的優劣，決策出最優解法，這是教師應培養學生掌握的重要能力。